基于改进DBSCAN算法的驾驶风格识别方法研究

万 豫, 黄妙华, 王思楚

(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室,湖北 武汉 430070; 2.汽车零部件技术湖北省协同创新中心,湖北 武汉 430070; 3.武汉理工大学 汽车工程学院,湖北 武汉 430070)

0 引 言

驾驶风格指驾驶员习惯的驾驶方式[1],用来表征在实车环境中对车辆操作的行为特征。通过对驾驶员驾驶习惯和车辆行驶数据的分析准确识别出驾驶员的驾驶风格,对于改善车辆的安全性、经济性和舒适性均有重要意义。

目前,针对驾驶风格的评测主要分为主观评测和客观评测2种[2]。主观评测包括专家打分、问卷调查等方式,但该方法受环境因素的影响较大,使用范围受限;客观评测主要基于实车实验或驾驶模拟器获得真实驾驶数据,通过对数据的分析来客观地评价驾驶风格。

对于驾驶风格识别的研究,国内外学者用了诸多方法。文献[3]通过主成分分析和层次聚类相结合的方法,根据多个主成分的聚类结果将驾驶员风格分为6类;文献[4]利用速度、加速度及节气门开度等参数提出了基于能耗最优化驾驶风格的分类方法,并将驾驶员分为保守型、一般型和激进型;文献[5]设计了一种模糊推理系统,将车辆纵向加速度与横向加速度的欧氏范数的平均值及车速作为系统输入,输出驾驶风格;文献[6]通过加速度的平均值及标准差之间的关系,将驾驶风格分为冷静型、正常型和激进型3种类型;文献[7]使用不同的分类器将驾驶风格分成激进和正常2种类型,并比较了随机森林、神经网络、k近邻以及决策树等算法的分类效果；文献[8]提出了一种基于k-means聚类的驾驶风格识别方法,并证明了该方法对乘用车和商用车2种车型均具有较好的识别效果;文献[9]建立驾驶风格识别数据库,利用k-means聚类方法和D-S证据理论决策融合方法进行聚类分析,提出的驾驶风格识别方法查准率达到80%;文献[10]通过主成分分析提取出表征混合动力汽车驾驶风格的特征参数,并应用k-means聚类方法对驾驶风格进行了聚类分析,最后利用支持向量机(support vector machine,SVM)算法对驾驶风格进行了识别,识别精度达到90%以上;文献[11]建立了个性化驾驶员模型,并提出了一种基于关联维数的驾驶风格指数用于评估驾驶的激进程度。

以上成果大多在驾驶模拟器或实车实验中获得,在记录数据时可以直接采集加速度、油门开度等数据项,同时数据采集周期可自由调控,大部分为1 s,因此可以直接对数据进行处理,从而识别驾驶风格。

随着以电动汽车为代表的新能源汽车数量日益增多,众多新能源汽车监管平台应运而生,实时记录大量新能源汽车的行驶数据[12]。因为车辆众多,数据量庞大,过短的数据采集周期会为数据的存储和处理等带来困难,且提高了成本,所以10、30 s成为常用的采集周期。相比于实车实验以1 s为周期采集到的数据,平台所记录的数据相对稀疏,造成了一定程度的信息缺失,因此,本文研究重点为如何利用长采集周期的数据准确评测驾驶风格。

通过武汉电动汽车大规模分时租赁与集成运营平台,本文共收集了自2017年7月至2018年6月间800 辆车的出行数据,车型为海马爱尚160EV,数据采集周期为10 s,设计了基于改进DBSCAN算法的驾驶风格识别方法,通过对车辆行驶加速度的聚类,完成驾驶风格的识别,并比较了不同采集周期的数据对结果的影响,最后从能耗等方面验证了本文识别方法的合理性。

1 整体思路

1.1 DBSCAN算法

DBSCAN算法是一种基于密度的聚类算法[13],通过一组邻域参数(ε,MinPts)来刻画样本分布的紧密程度。给定数据集D={x1,x2,…,xm},定义如下主要概念:

(1)ε-邻域。对于xi∈D,其ε-邻域包含样本集D中与xi距离不大于ε的样本,即

Nε(xi)={xi∈D|dist(xi,xi)≤ε}。

(2) 核心对象。若xi的ε-邻域至少包含MinPts个样本,即|Nε(xi)|≥MinPts,则xi是一个核心对象。

DBSCAN算法示意图如图1所示。

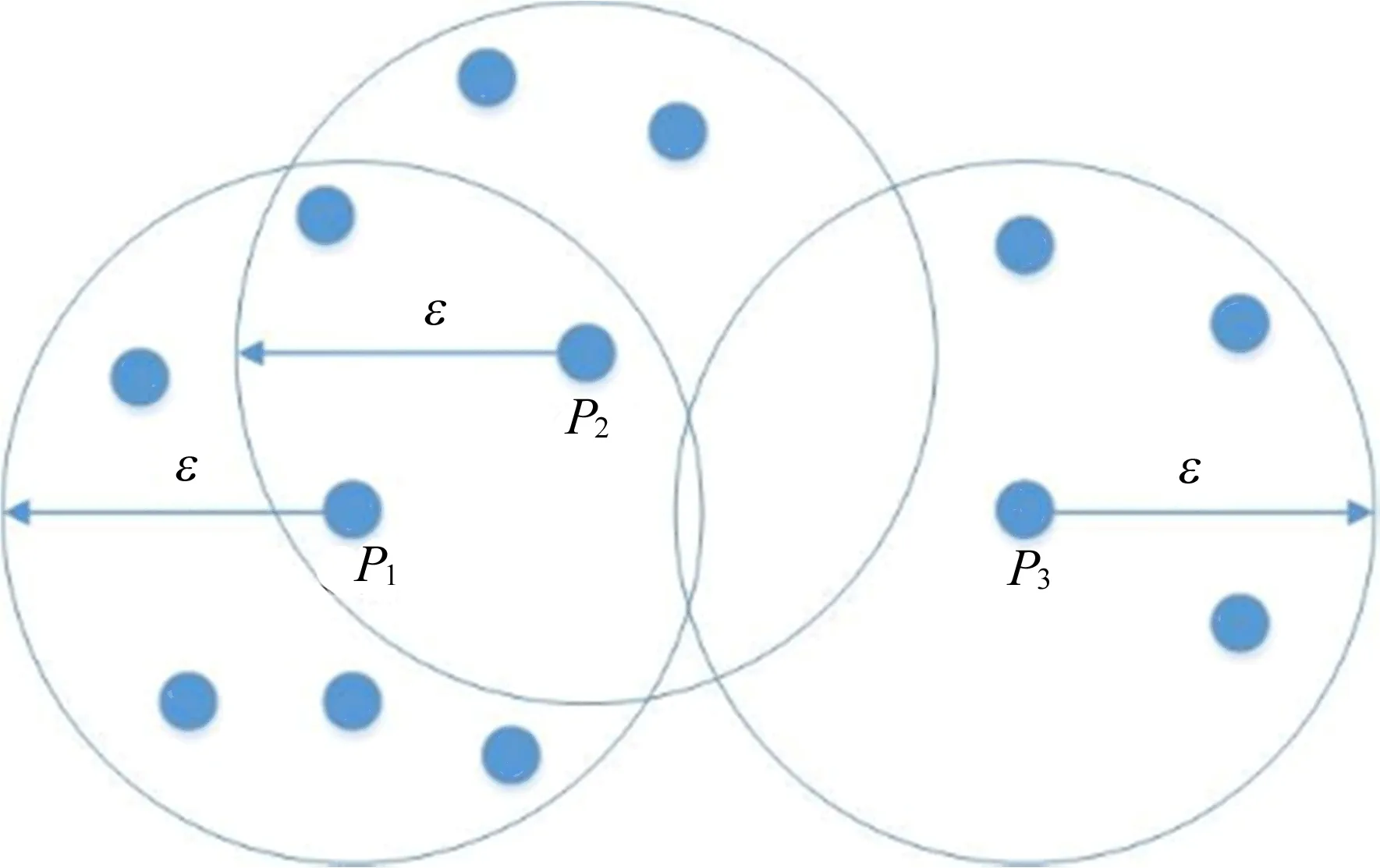
图1 DBSCAN算法示意图

若规定MinPts=5,则样本P1为核心对象,P2为非核心对象,P3为离群点。

1.2 驾驶风格识别流程

DBSCAN算法的结果是将样本点划分成核心点、非核心点和离群点,而车辆行驶过程中加速、减速的样本可以与此相对应。大部分情况下,加速、减速的值均在合理范围内,驾驶员驾驶风格的不同导致急加速、急减速样本数量的比例不同,风格越激进,急变速的比例越高,可将急变速点视为离群点。通过对车辆行驶数据的聚类,将变速行为分别与核心点、边界点和离群点相对应,从而对驾驶风格做出评测与分类。具体步骤如下:

(1) 对原始数据进行预处理[14],剔除缺失数据及噪声数据,利用速度差与时间差计算每种速度下的加速度,得到速度-加速度(v-a)点。

(2) 基于DBSCAN算法对速度-加速度点进行聚类,得到核心点、边界点和离群点。

(3) 利用多项式拟合边界点,得到急变速边界。

(4) 通过变速边界线将所有数据点分为合理变速点和急变速点2类。定义急变速点占总数据点的比例为驾驶风格评分。驾驶风格越激进,急变速点越多,相应的驾驶风格评分越大。

此外,速度范围在0～20 km/h内的数据点较密集,聚类后核心点比例过高;某些车辆速度大于100 km/h的数据点太过稀疏,聚类后离群点较多。因此最终选用速度范围在20～100 km/h之间的数据点作为处理对象。

2 算法改进及风格识别

2.1 DBSCAN算法改进

在用DBSCAN算法对v-a点聚类时,样本数量和数据分布会对分类结果产生一定影响,造成结果缺乏合理性和准确性,本文从参数和权重2个方面对算法进行改进。

2.1.1 参数改进

在DBSCAN算法中,MinPts表示ε-邻域内样本个数的阈值,样本个数多于MinPts即为核心点。但随着总样本个数的增加,满足核心点条件的样本点逐渐增多,只有通过改变ε、MinPts才可维持结果的稳定。为了减少样本总数对结果的影响,现将核心对象的定义改变为:若xi的ε-邻域至少包含MinPts个样本,即

|Nε(xj)|≥MinPts/ND

(1)

其中,ND为总样本数;xi为一个核心点。

改进前、后聚类结果随样本数量变化的情况如图2所示。

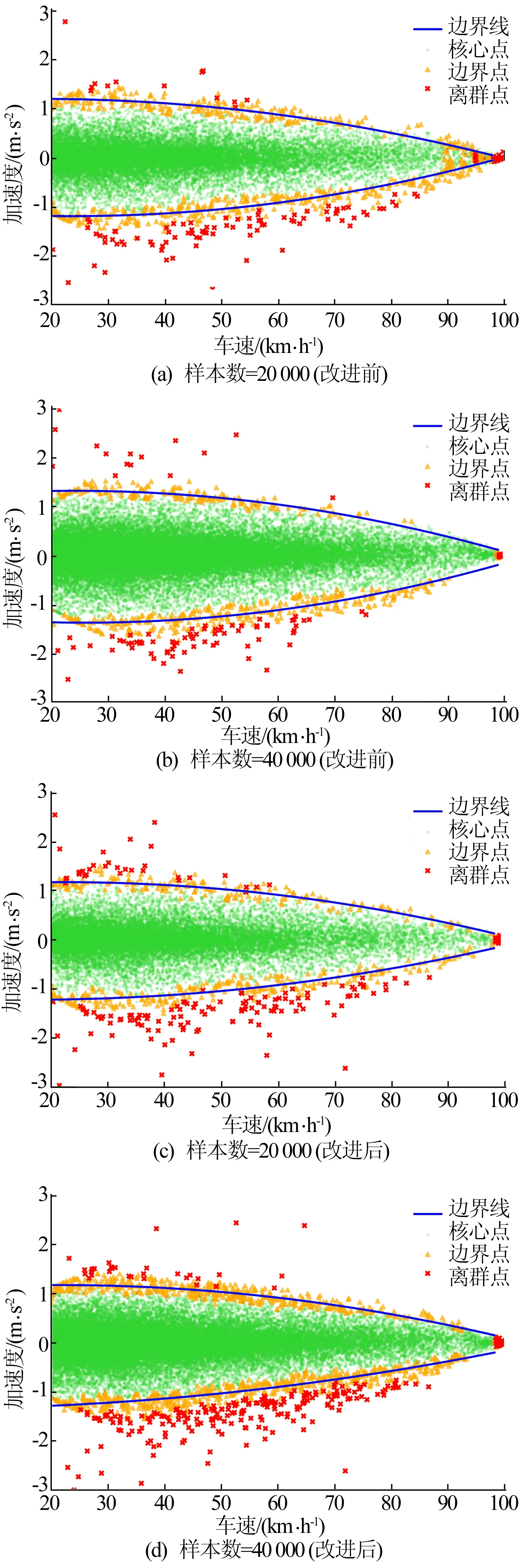
图2 改进前、后样本数量对聚类结果的影响

由图2a、图2b可知,当样本个数由20 000变为40 000时,急变速边界线产生了外扩,这是由于随着样本数目的增加,更多的样本点从非核心点转变为核心点,边界线也随之移动,造成了结果的波动。

由图2c、图2d可知,既使样本数目增加,边界线也基本相同。

2.1.2 对区间样本数量及加速度权重的改进

密度聚类的优点在于能够自主地区分出核心对象与离群点,但有时数据的分布会对结果产生较大的影响。

第23辆车的聚类效果如图3所示。由图3可知,当速度区间为70～100 km/h时,出现了大量的离群点,其主要原因是此车大部分时间为低中速行驶,速度在70 km/h以内,70～100 km/h区间的数据点较少,因此区间中的数据分布稀疏,密度较低,经过聚类处理后被划分为离群点。

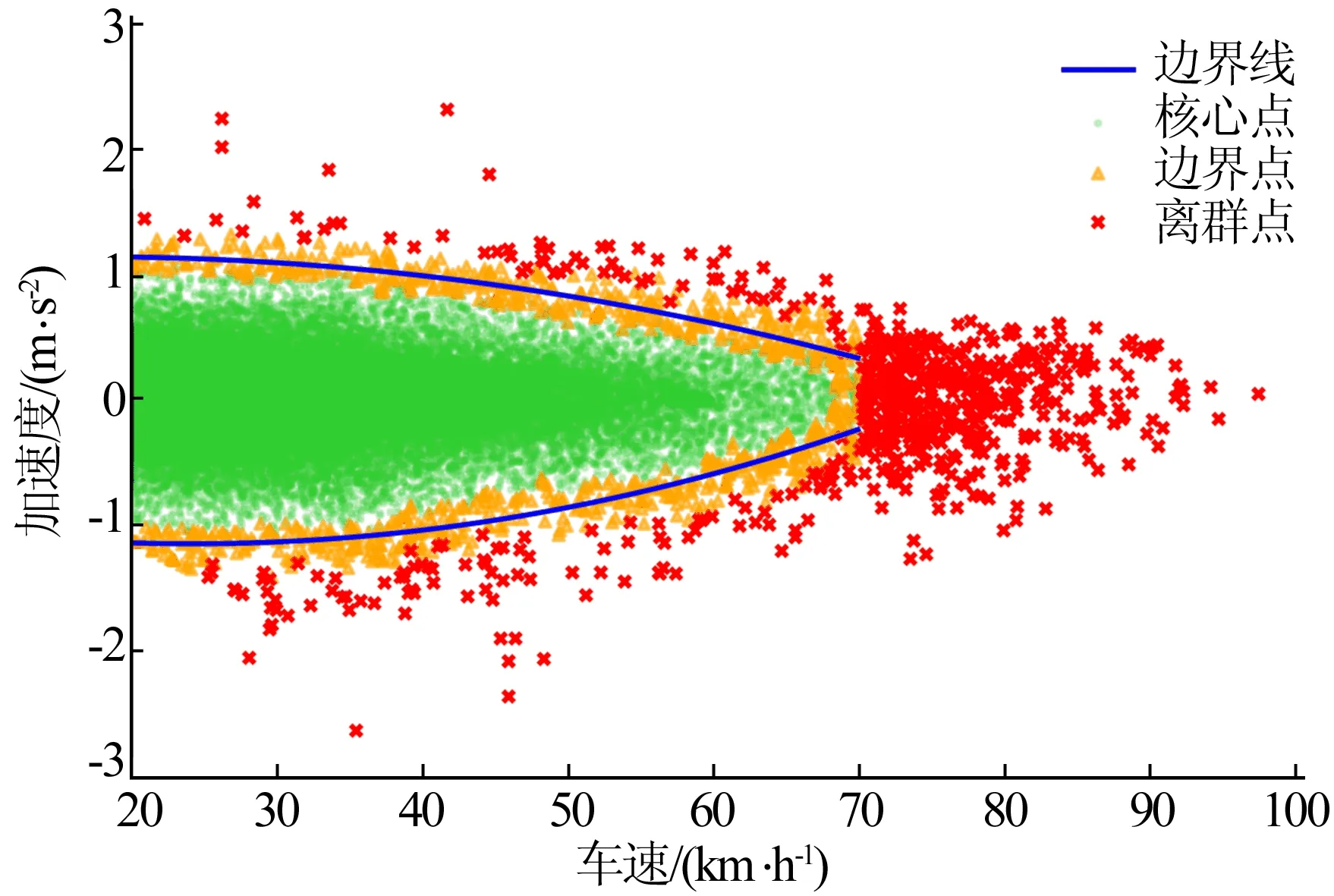
图3 数据分布引起的聚类异常

此类缺陷是由样本数据固有分布造成的,车辆的行驶环境不同,v-a样本点的分布会有很大的不同,不能保证在每个速度区间的样本数基本相同,而样本数较少的区间由于样本密度低而倾向出现更多的离群点。

此外,加速度绝对值的大小也会对聚类结果产生影响。绝对值越大,越倾向于离群点。若忽视加速度绝对值的影响,则可能出现某一辆车加速度平均值和标准差均很小,但聚类后离群点却很多,导致驾驶风格评分很大的情况。

针对上述2个问题,现赋予每个样本点不同的权重。

对于不同速度区间的样本点,为了消除样本分布差异带来如图3中的影响,可提高样本分布稀疏区间内数据点的权重值,即在某一区间内的样本越少,其权重越高。这样可以在不改变ε、MinPts 2个参数的前提下,实现不同速度区间内样本聚类标准的统一,不会出现因区间内样本较少而离群点大大增加的情况。

每个区间内样本的权重由该区间内的样本数量与样本总数所决定。设样本总数为N,按照速度区间划分为[20,25)、[25,30)……[95,100)等m个区间,本文取m=16,全体样本在每个区间的样本数依次为ni(i=1,2,…,6),则每个区间样本权重为:

(2)

归一化处理后得到样本权重W1为:

(3)

若样本j的加速度为aj,则其幅值权重W2为:

W2=c/aj

(4)

其中,c为幅值系数,通过改变c的取值可改变不同样本点成为离群点的趋势,离群点的比例随着c的增大而增大。普遍而论,驾驶员在驾驶汽车的过程中,急变速行为是少数,因此c不宜取值过大。经过多次尝试,当c取值为10时,样本划分较为合理。

权重越大,越趋向于成为核心点;权重越趋近于0,越易成为离群点。当权重为1时，与未加权重的原算法等效。

综合2个权重,并考虑到当区间样本数量很小导致权重过大的情况,确定最终权重W为:

(5)

2.2 驾驶风格识别

为了减小时间开销,首先确定识别驾驶风格需要的最小样本数。本文用驾驶风格评分的平均值和标准差来描述稳定性。通过编写python程序设置不同的样本数进行识别,且为了保证结果的稳定性,在每个样本数下循环识别多次,比较结果平均值和标准差的变化,待两者稳定时,即为最小样本数。

设置样本数为5 000～80 000,依次增长1 000,并在每个样本下运行30次,标准差和平均值随样本个数变化的关系如图4所示。

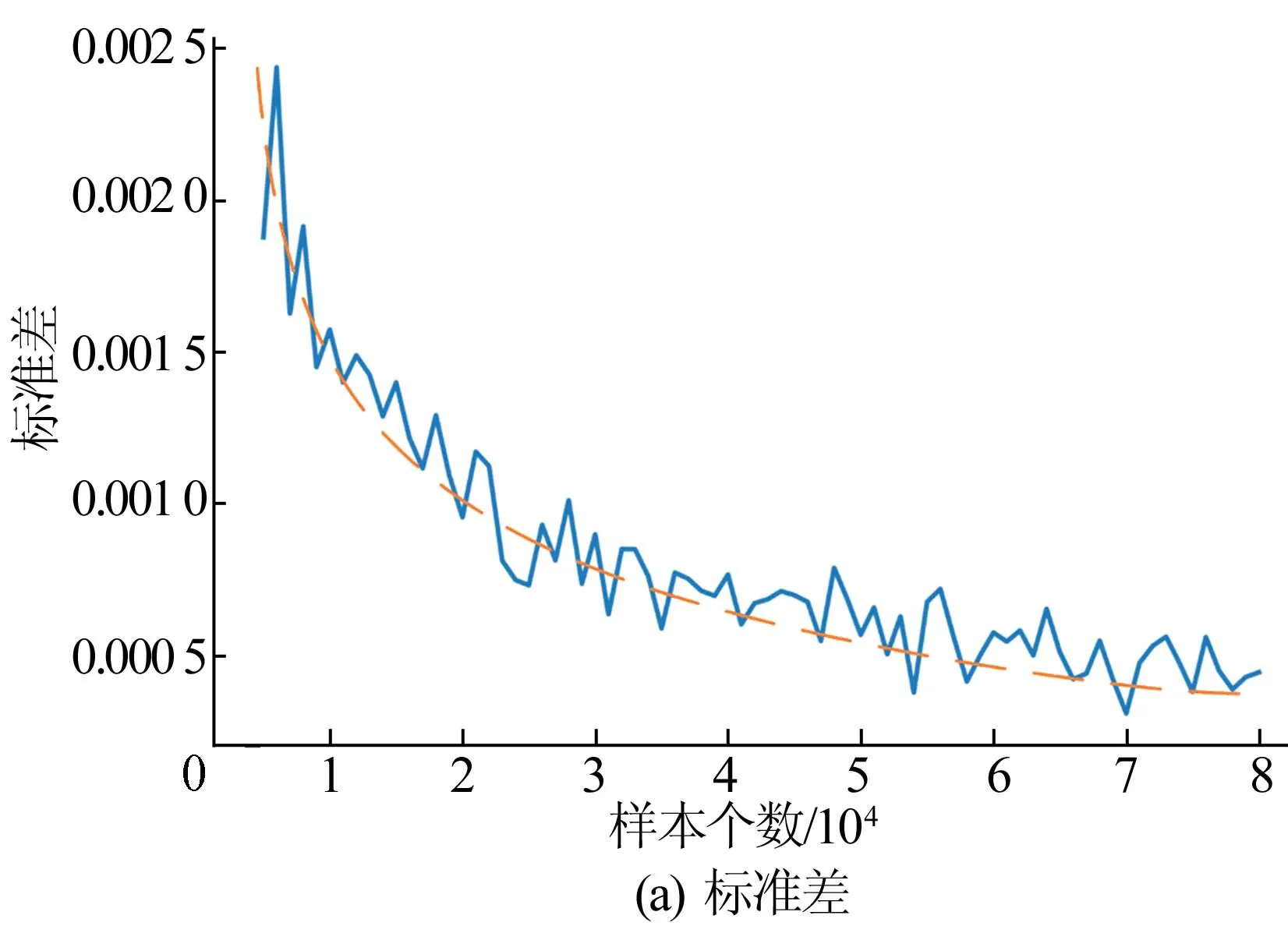
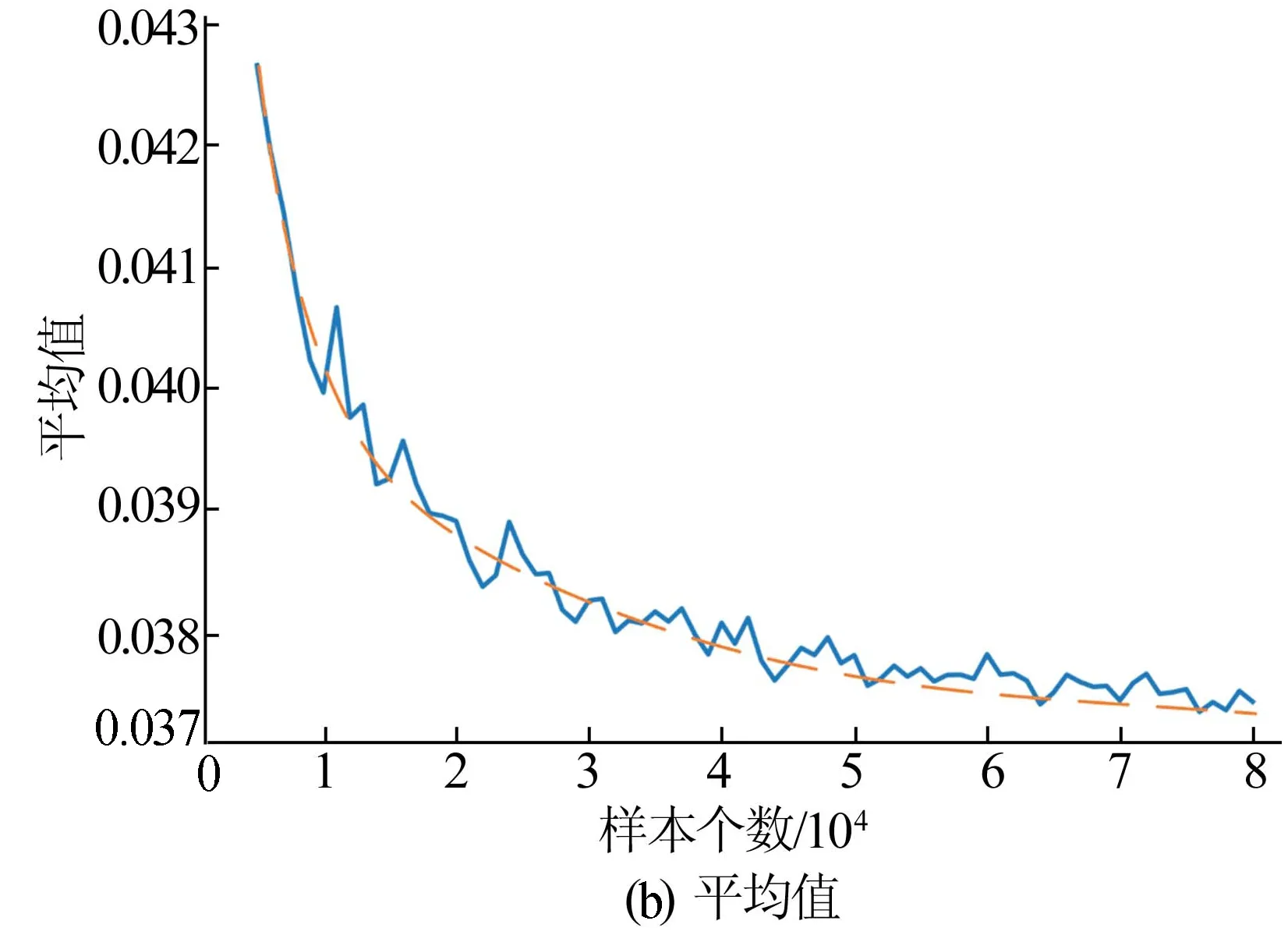
图4 评分标准差、平均值与样本个数的关系

由图4可知,标准差与平均值的变化趋势基本相同,当样本数小于20 000时,随着样本数量的增长,平均值与标准差呈快速下降趋势;当样本数大于20 000时,两者虽仍在减小,但逐渐趋于稳定。因此取20 000为每次识别的样本个数。

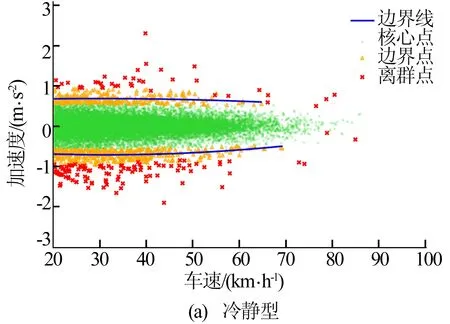
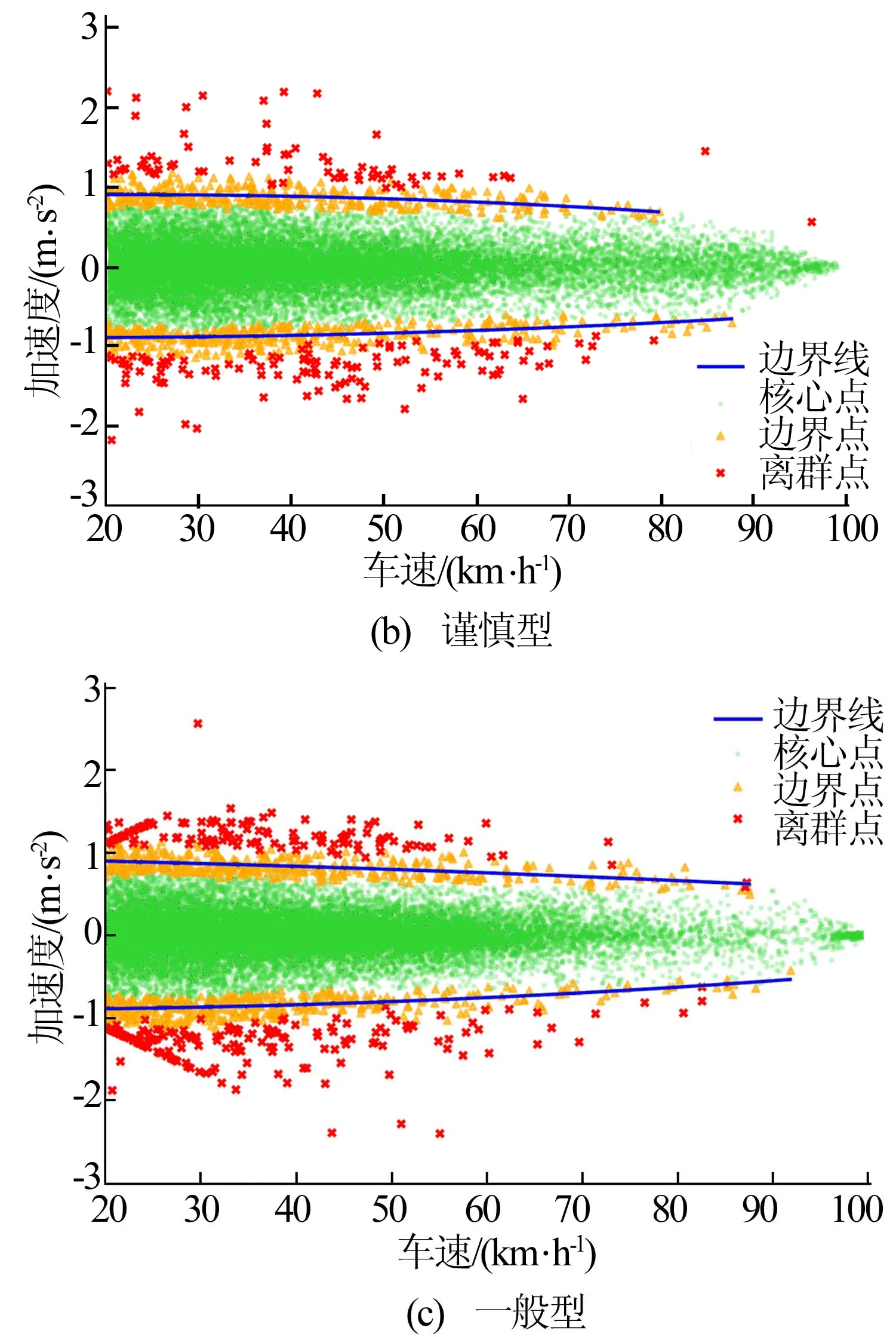
对800辆车的行驶数据进行预处理,删除异常值与缺省值,并基于改进的DBSCAN算法识别驾驶风格。算法参数的确定具有一定的主观性,理论上没有硬性条件规定参数的值,只要保证经聚类算法后得到的核心点、离群点和边界点分布符合常理,且每辆车需在同一参数条件下进行识别即可。通过观察聚类点的分布,确定参数统一取值为ε=0.4、MinPts=0.07后,即可得到每辆车急变速点的数量,进而求出驾驶风格评分,最终得到了741辆车的有效识别结果。在这741辆车的风格得分中,最小的是0.002,最大的是0.220,为了更加细致地描述驾驶风格,现根据风格评分将741名驾驶员分为5类,具体见表1所列。每种风格类型的聚类效果如图5所示。

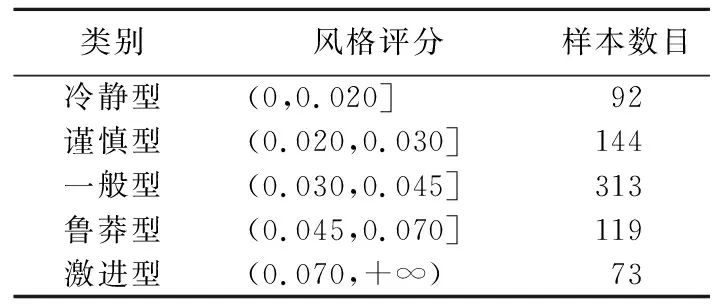
表1 驾驶风格分类

3 数据采集周期对识别结果的影响

新能源汽车检测平台的数据采集周期一般为10、30 s,相对于实车实验周期较长,计算加速度时时间间隔较大,可能导致计算结果不准确。现利用平台上11月1日至11月15日9辆车的行驶数据,数据采集周期为1 s,探究采集周期对驾驶风格识别结果的影响。

利用每秒采集的数据,每隔10 条和30 条数据抽取1条,即可获得采集周期分别为10、30 s的数据。

3种周期下的v-a图如图6所示。

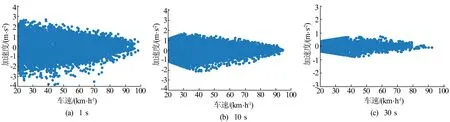
图6 不同采集周期下的v-a分布

由图6可以看出,在不同周期下,加速度点分布基本相同,均随着速度的增大,最大加速度呈减小趋势。不同的是,相比于长周期采集,每秒采集的数据点更加发散,极值更大。下面分别从平均值、标准差等统计参数和驾驶风格评分排序2个方面探究数据采集周期的影响。

3.1 数据采集周期对平均值、标准差的影响

针对3种不同的采集周期,分别计算车辆行驶的平均速度vave、平均加速度aave+、平均减速度aave-、加速度标准差astd+、减速度标准差astd-。不同采集周期下各参数的对比结果见表2所列。

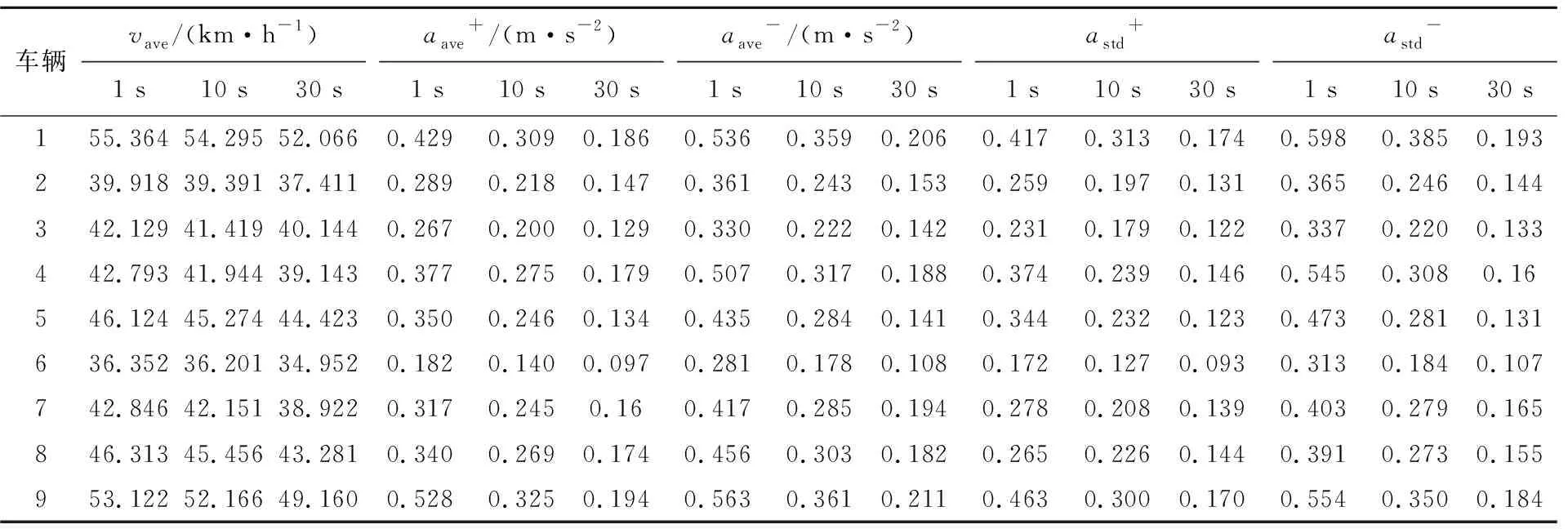
表2 不同采集周期下的统计参数

不同周期下统计参数之间的倍数关系如图7所示。

由图7a可知,虽然10 s采集周期的结果不能完全替代1 s,但两者之间存在一些相关关系；平均值方面,两者的平均速度基本相同,1 s数据的加速度和标准差约为10 s数据的1.3倍,减速度和标准差约为10 s数据的1.5倍。

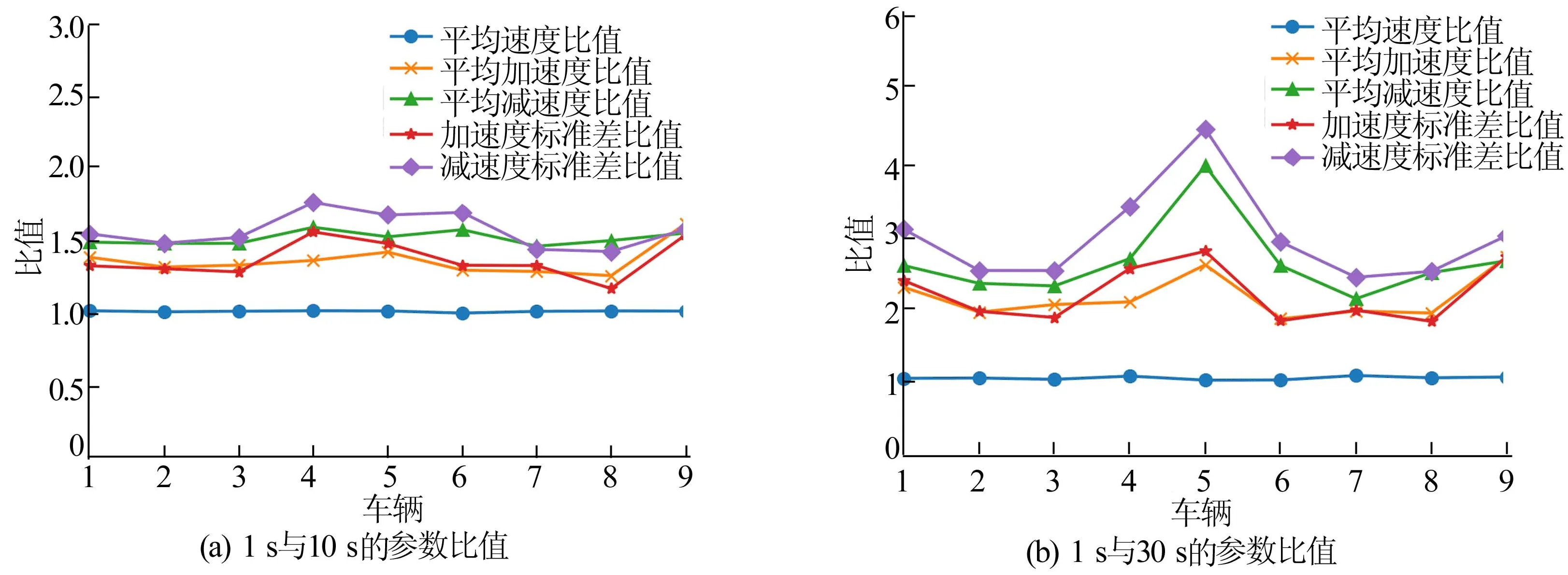
图7 不同采集周期下的参数比值关系

从图7b可以看出,当数据采集周期增长至30 s时,除平均车速外,各参数比值均出现较大的波动,不能准确反映出车辆驾驶时加速、减速的真实情况,信息损失严重,无法做出准确的风格识别。

由此可见,10 s数据在一定程度上可以反映1 s数据的分布,但当周期增至30 s时,结果将会出现较大误差。

3.2 数据采集周期对驾驶风格识别的影响

不同的周期下采集的数据分布情况不同,周期越短,加速度分布越发散。在识别驾驶风格时,若保持算法参数不变,30 s周期下的数据过于密集,部分车辆只有核心点,无法识别风格。因此只比较1 s和10 s 2种数据采集周期对识别结果的影响。

采用改进的DBSCAN算法对2种不同采集周期下的数据进行驾驶风格识别,得到的结果见表3所列。

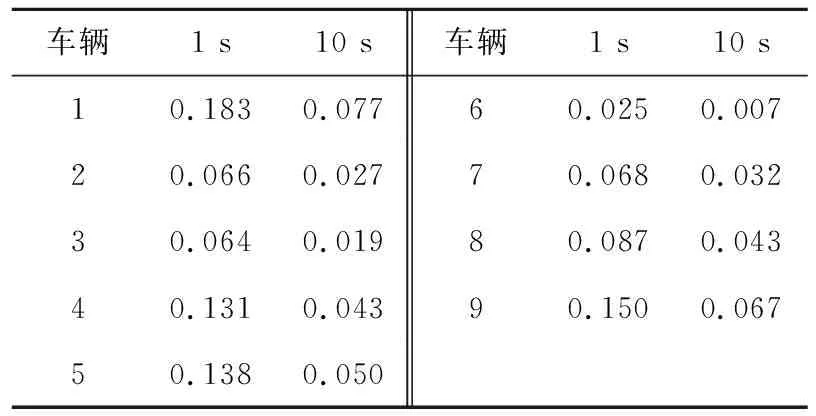
表3 不同采集周期下的驾驶风格评分

从表3可以看出，采集周期为1 s时,9辆车风格评分从高到低依次为1、9、5、4、8、7、2、3、6;10 s周期下,9辆车的风格评分从高到低依次为1、9、5、8、4、7、2、3、6。可以发现虽然分数不相同,但在2种周期下所得结果的排序基本相同,只有车辆4和车辆8的顺序发生了调换。因此对10 s数据进行驾驶风格识别所得到的结果能够代替1 s的结果。

4 结果分析

分别计算车辆运行数据的统计参数与能耗值,并与改进前算法进行对比,验证本文所提出的驾驶风格识别方法的有效性。

根据上文所分类别,分别计算各类风格的统计参数值,得到的结果见表4、表5所列。

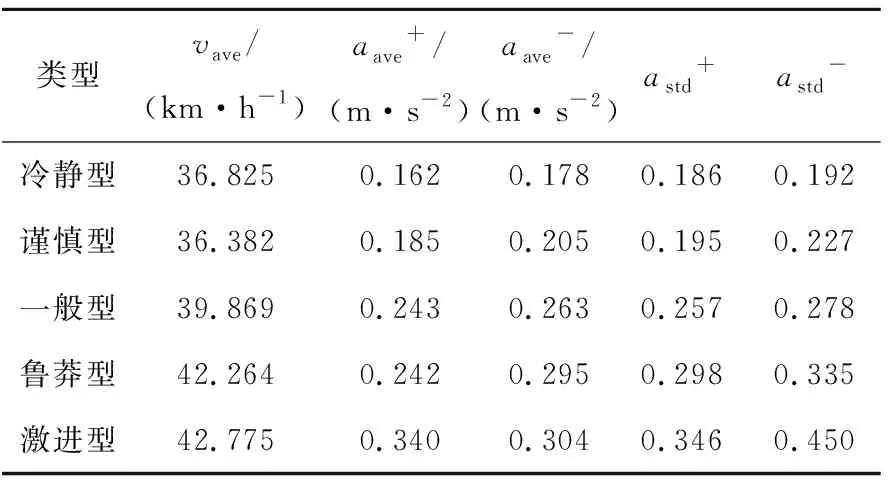
表4 算法改进前不同驾驶风格的统计参数

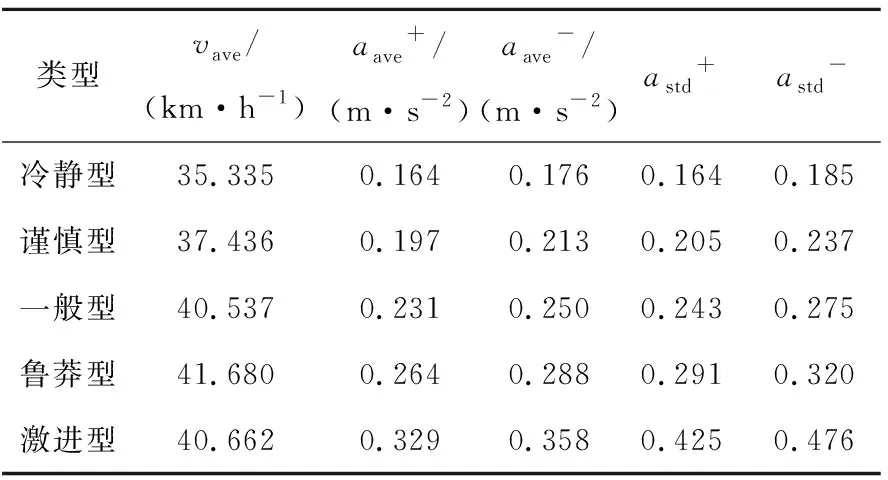
表5 算法改进后不同驾驶风格的统计参数

利用充电状态、SOC值和累积里程等数据项,计算出车辆2次充电间的行驶里程及耗电量,进而得到每次出行的能耗值[15]。每种风格的能耗平均值如图8所示。

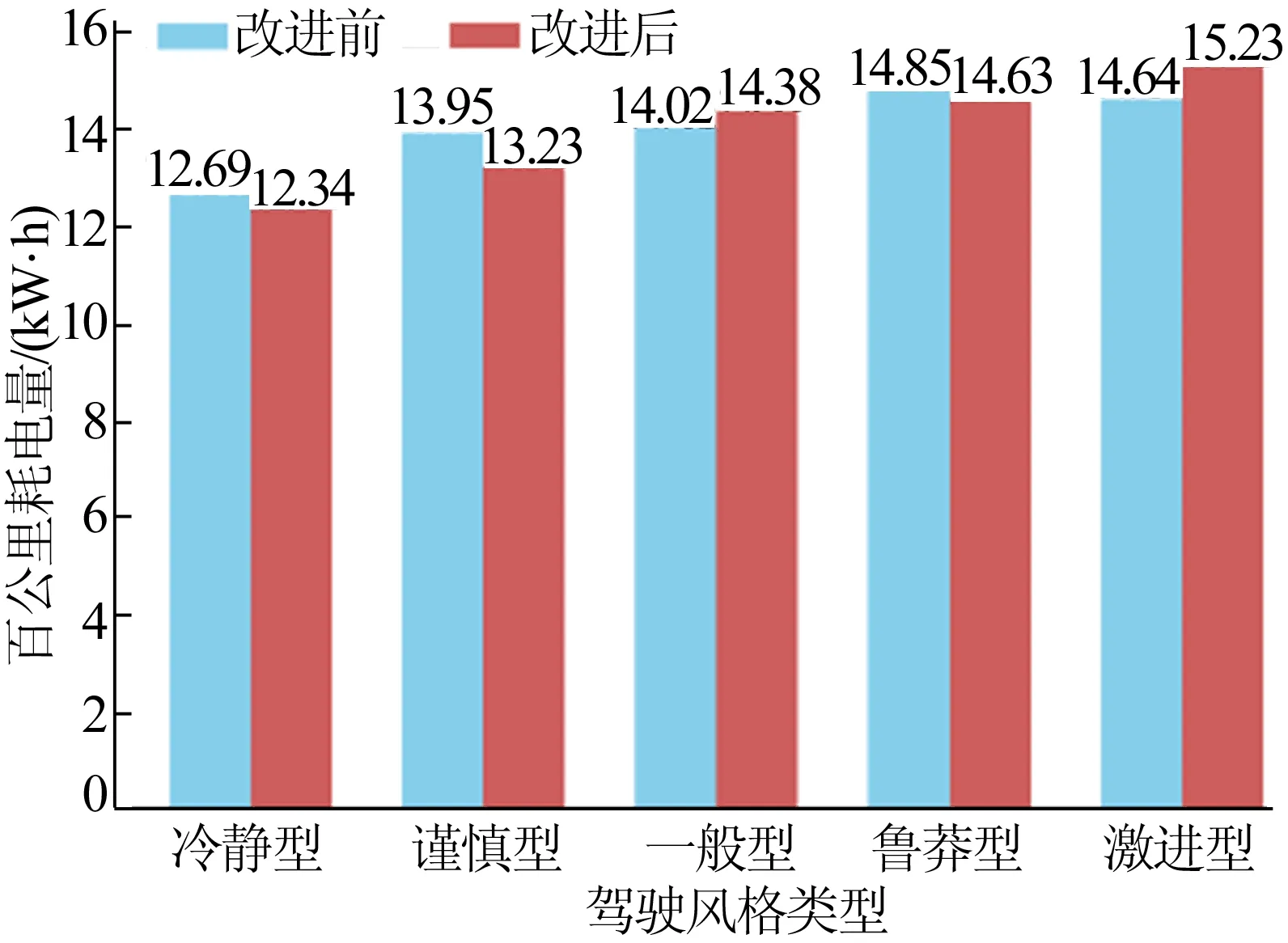
图8 算法改进前、后不同类型驾驶员能耗值

从图8可以看出,随着驾驶风格越来越激进,从冷静型到激进型,速度均值、加速度均值、减速度均值、加速度标准差、减速度标准差都是从小到大,且相差数值较为稳定,这与越激进的驾驶风格越倾向于急加速和急减速的定义是一致的；此外,不同风格的能耗值也随之增加,与人们对驾驶风格的定性认知相吻合[16-17]。因此本文采用改进的DBSCAN算法对驾驶风格进行识别是合理的。

改进前算法虽然可以得到类似结论,但不同驾驶风格的同一统计参数变化较为模糊,不能将不同风格的车辆完全区分。另外,利用改进前算法所得的风格分类能耗图也不理想(谨慎型的能耗大于一般型),与定性认知相悖,由此可证明本文算法改进的有效性。

5 结 论

本文提出了一种识别驾驶风格的方法,实现了对741辆车驾驶风格的识别与分类,主要得到以下结论:

(1) 对DBSCAN算法从参数和权重2个方面改进,弥补了样本数量和车速差异带来的影响,并用改进后的算法计算得到驾驶风格评分,根据评分将驾驶风格分为冷静型、谨慎型、一般型、鲁莽型和激进型5类。

(2) 在1、10 s 2种数据采集周期下,平均速度、平均加减速和标准差均呈倍数关系,9 辆车的驾驶风格评分排序也基本相同,因此可以用10 s的数据代替1 s数据进行风格识别。但当采集周期增至30 s时,结果便出现较大误差。

(3) 计算741辆车的统计参数和能耗值,风格越激进,平均速度、平均加速度、车辆能耗均增加,证明了风格识别的合理性。

本文研究还存在一定的不足,主要体现在只根据驾驶员的加速、减速行为进行驾驶风格的识别,因素过于单一,转向、变道等还未考虑其中;其次未能将风格的识别结果和车辆行驶的安全性联系在一起。这些工作有待进一步研究。