基于ICSO模糊PID控制的直线电机控制研究

程仕祥, 夏 链, 韩 江

(合肥工业大学 机械工程学院,安徽 合肥 230009)

0 引 言

永磁同步直线电机(permanent magnet linear synchronous motor,PMLSM)由于其结构简单、适合高速直线运动、易于调节和控制、适应性强、高加速度等特点被广泛地应用于工业、民用、军事及其他各种直线运动的场合。虽然传统PID控制具有算法简便、稳定性好、鲁棒性较强等优点,但由于是线性控制方法,不能适应PMLSM非线性系统动、静态性能的要求。模糊控制是智能控制的一个分支,可以实现参数的实时整定,在线调整PID控制的各个系数,具有控制灵活、自适应性强、控制精度高等优点,尤其适合PMLSM这种非线性、时变系统[1]。但是按常规方法设计的模糊控制器无法根据系统的运行状况和环境的变化进行自动调整,因此,其控制性能在大范围内得不到有效保证。鸡群算法[2](chicken swarm optimization,CSO)是一种模拟具有等级秩序的鸡群觅食行为的全局优化算法,该算法具有较快的收敛速度、较高的收敛精度及较强的鲁棒性能。

本文将模糊控制与PID结合起来,设计一种模糊PID控制器,采取改进鸡群算法(improved chicken swarm optimization,ICSO)优化模糊控制器中的参数,并作用于PMLSM伺服系统的位置环,以便实时调整PID参数Kp、Ki、Kd。结果表明,ICSO-FUZZY-PID控制器具有传统PID控制器所不具备的优越性,从而使PMLSM系统能实现更好的控制效果。

1 PMLSM的数学模型

PMLSM是多输入多输出、具有时变性和多变量耦合的非线性系统,多采用矢量控制的方法,根据矢量控制的基本原理,采用d轴电流id=0的控制策略,PMLSM的数学模型[3]可简化为:

(1)

(2)

(3)

其中,L为电感;iq为q轴电流;Rs为初级(动子)绕组等效电阻;Ke为电机反电动势系数;v为初级线速度;uq为q轴电压;τ为永磁体极距;φf为永磁体励磁基波磁链;m为电机的初级质量;Kf为电机电磁推力系数;Fd为总阻力大小;B为黏滞摩擦系数,黏滞摩擦系数与电机的运行速度等参数相关,由于直线电机采用滑轨支撑,黏滞摩擦力比较小[4],在本文中不作为研究重点,为方便研究,本文将黏滞摩擦系数B设为定值。

2 单轴伺服系统仿真建模

本文的研究对象为水平交叉布置的PMLSM数控系统实验平台的X轴部分,旨在减小其跟踪误差,提高控制精度。

PID控制是传统控制中最具代表性的一种控制方法,应用也最为广泛。以实验平台的X轴为例,直线电机主要性能参数如下:质量m=5 kg;黏性摩擦系数B=1.2 N/(m·s-1);推力常数Kf=54.5 N/A;反电动势常数Ke=29.3 m/s;时间电气常数=0.7 ms;电感L=4.4 mH;极距2τ=32 mm;电阻R=13.4 Ω;热阻Rth=0.8 ℃/W。直线电机伺服控制系统的位置环采用PID控制,速度环采用PI控制,电流环采用P控制。为了便于分析和研究,将电流环视为一个增益常数Kc。根据直线电机伺服系统的工作原理,在Matlab/Simulink中搭建X轴单轴伺服系统的仿真模型,如图1所示。

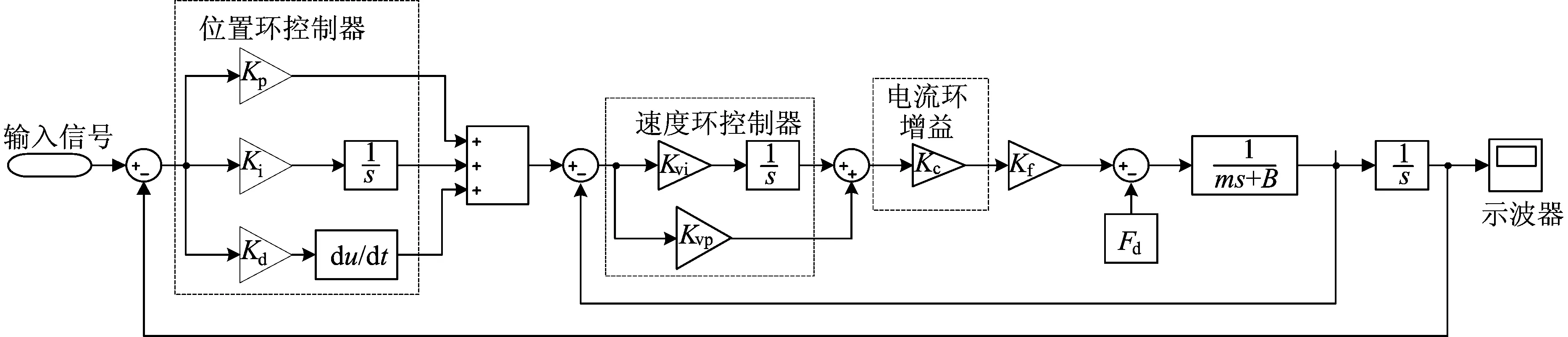
图1 PMLSM X轴伺服系统仿真模型

3 位置环模糊PID控制器的设计

本文所研究的直线电机速度环和电流环均设置在驱动器中,而驱动器中的控制模型是不变的,因此可将驱动器和PMLSM视为广义的研究对象,以下均简称为PMLSM 驱动系统。本文在直线电机伺服系统位置环以模糊PID控制器代替传统PID控制器,其原理框图如图2所示。

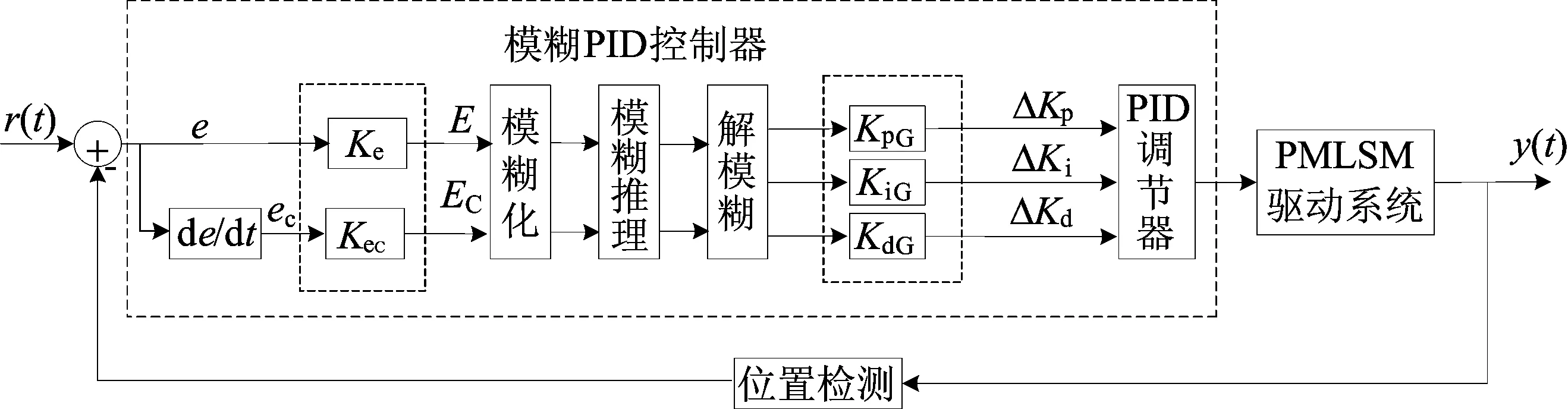
图2 PMLSM系统模糊PID控制结构

在图2所示的模糊PID控制器构成的PMLSM伺服系统中,选取直线电机运行过程中的跟踪误差e、跟踪误差变化率ec=de/dt作为模糊控制器的输入信号,模糊控制器的输出[5-6]是ΔKp、ΔKi、ΔKd。输入变量和输出变量被标准化到[-3,3],即跟踪误差e和误差变化率ec从基本论域分别乘以量化因子Ke、Kec,变换至对应的模糊论域E[-3,3]和EC[-3,3],在完成模糊化处理后,将获得的模糊量作为模糊推理系统的输入;利用依据专家经验建立的模糊规则进行模糊推理,获得模糊量;再通过解模糊,将解得的模糊量转换为精确的输出量;最后再将输出量对应乘以比例因子KpG、KiG、KdG,得到比例系数、积分系数、微分系数的调节量ΔKp、ΔKi、ΔKd。模糊语言变量设计为:输入变量模糊论域E、EC和输出变量ΔKp、ΔKi、ΔKd的语言值均设置为7个,即{NB(负大),NM(负中),NS(负小),ZO(零),PS(正小),PM(正中),PB(正大)}[7]。输入、输出隶属度函数采用形式简单、计算效率高的三角形隶属函数的形式,具体如图3所示,其中变量F代表E、Ec、ΔKp、ΔKi、ΔKd。

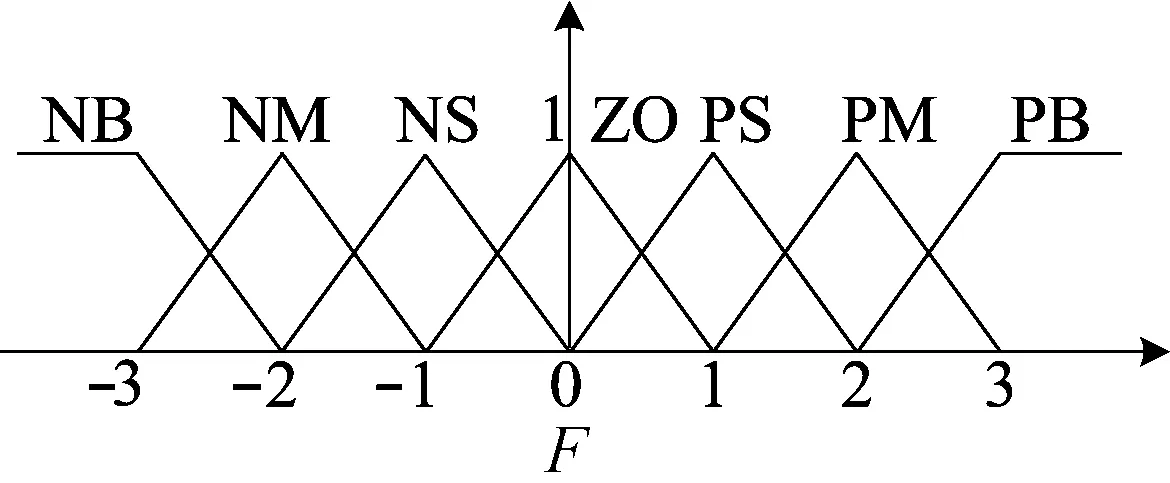
图3 输入、输出的隶属度函数

结合Mamdani模糊推理,建立Mamdani型模糊系统[8]。利用面积中心法解模糊,将所得结果对应乘以比例因子KpG、KiG、KdG,最终转化为比例系数、积分系数、微分系数调节量的精确值ΔKp、ΔKi、ΔKd。将所得的ΔKp、ΔKi、ΔKd与初始的PID参数Kp0、Ki0、Kd0对应相加，得到最终的PID控制参数,即

(4)

3 ICSO优化模糊PID控制器的设计

按照一般公式计算得到的量化因子和比例因子的控制效果并不好,通常需要用试凑法反复调整它们的取值,以得到最佳的控制效果。然而反复调整的过程不仅浪费时间,而且不能保证得到的就是最佳的控制器参数[9]。针对这一情况,引入CSO算法来优化模糊控制器中的量化因子和比例因子,进而间接改变模糊控制器的控制规则和隶属函数,实现对模糊控制器中参数的最佳调整,达到较理想的控制效果。

假定鸡群搜寻食物的空间范围为D维,鸡群总量为N,其中公鸡数目为Ng、母鸡数目为Nm1、小鸡数目为Nx、妈妈母鸡数目为Nm2。整个鸡群中,公鸡的觅食能力最强,但适应度最低;小鸡的觅食能力最差,但适应度最高;母鸡的觅食能力一般。因为公鸡、小鸡、母鸡这3类鸡各自的食物搜索能力存在明显差异,所以相应采取不同的位置更新方法。

在每次迭代过程中,首先更新公鸡位置。公鸡对应的位置更新规则为:

xi,j(t+1)=xi,j(t)[1+Randn(0,σ2)]

(5)

(6)

其中,xi,j(t+1)、xi,j(t)分别为第i只公鸡j维空间中第t+1次和第t次迭代时位置;Randn(0,σ2)代表均值为0、标准差为σ2且正态分布的随机数;ε为一个很小的常数，但不等于0;k为随机选取的第k只公鸡(不含i);fi、fk分别为第i只和第k只公鸡适应度大小。

母鸡的伙伴公鸡位置以及其他公鸡、母鸡对当前母鸡的位置更新影响较大,在公鸡位置更新后更新母鸡位置。母鸡对应的位置更新规则为:

xi,j(t+1)=

xi,j(t)+C1Rand(xu,j(t)-xi,j(t))+

C2Rand(xv,j(t)-xi,j(t))

(7)

(8)

C2=exp(fv-fi)

(9)

其中,xi,j(t+1)、xi,j(t)分别为第i只母鸡在j维空间中第t+1次和第t次迭代位置;Rand为[0,1]之间均匀分布的随机数;u为从第i只母鸡所在鸡群内随机选取的第u只公鸡;C1为伙伴公鸡u对第i只母鸡的影响因子;v为在公鸡和母鸡中随机选取的第v只个体,但u不等于v;C2为其他公鸡、母鸡对第i只母鸡的影响因子;fu、fv分别为第u只、第v只公鸡的适应度。

小鸡在更新当前位置时,不仅受到小鸡妈妈位置信息的影响,同时还受到鸡群中具有最强觅食能力的公鸡位置信息的影响。因此,在小鸡的原位置更新公式中,引入小鸡的自学习系数及小鸡跟随公鸡的学习因子。在母鸡位置更新后更新小鸡位置,改进后小鸡对应的位置更新规则为:

xi,j(t+1)=

Bxi,j(t)+H(xm,j(t)-xi,j(t))+

M(xn,j(t)-xi,j(t))

(10)

其中,xi,j(t+1)、xi,j(t)为第i只小鸡在j维空间中第t+1次和第t次迭代时位置;B为小鸡的自学习系数;xm,j(t)为第i只小鸡的妈妈母鸡m在第t次迭代时的位置;H为妈妈母鸡位置对第i只小鸡位置的影响因子,取值区间为[0, 2];M为小鸡跟随公鸡的学习因子;xn,j(t)为妈妈母鸡所在鸡群中公鸡n在第t次迭代时的位置。

基于ICSO算法,选取时间乘以误差绝对值积分ITAE作为目标函数,目标函数为:

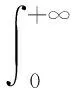
(11)

其中,e(t)为跟踪误差；t为时间。同时定义鸡群个体的适应度函数Fit=1/J。对上述模糊PID控制器中的量化因子Ke和Kec以及比例因子KpG、KiG、KdG进行优化。当目标函数寻优求解得到最小的J值时,即得到相应的最优模糊控制器参数Ke、Kec、KpG、KiG、KdG。

4 仿真与实验分析

4.1 仿真分析

在Matlab/Simulink中建立PMLSM系统模糊PID控制的仿真模型,再用Matlab编写ICSO算法优化模糊PID控制器的程序。ICSO算法参数如下:鸡群规模N=100,其中公鸡数目Ng、母鸡数目Nm1、小鸡数目Nx、妈妈母鸡数目Nm2分别为15、70、15、35;最大迭代次数为300;优化问题维数D=5,小鸡的自我学习系数B=0.3;小鸡跟随公鸡的学习因子M=0.85;妈妈母鸡对小鸡的影响因子H=0.75。设定所要优化的5个参数初始值为:量化因子Ke=1,Kec=1;比例因子KpG=1,KiG=3,KdG=5,各因子分别在[0,2]、[0,2]、[0,20]、[0,20]、[0,10]范围内寻优。系统中的位置环传统PID控制器的初始参数Kp0、Ki0、Kd0分别为90、18、6,速度环传统PI控制器的参数Kvp、Kvi分别为50、0.3；电流环增益Kc为0.25;设定系统所受阻力Fd=100 N,仿真时间为1 s。对本系统的位置环先后采取传统PID控制器及本文设计的ICSO-FUZZY-PID控制器,进行相同条件下的单位阶跃运动仿真。

PMLSM系统在空载运行情况下位置响应仿真对比结果如图4所示,目标函数最优解随进化迭代次数的变化如图5所示。

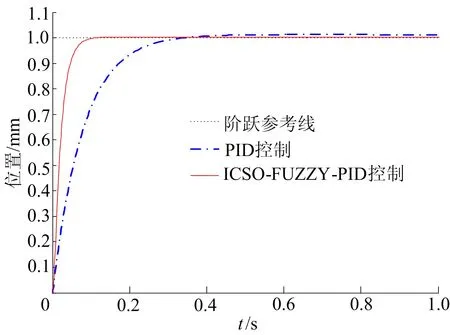
图4 ICSO-FUZZY-PID和PID位置控制仿真比较

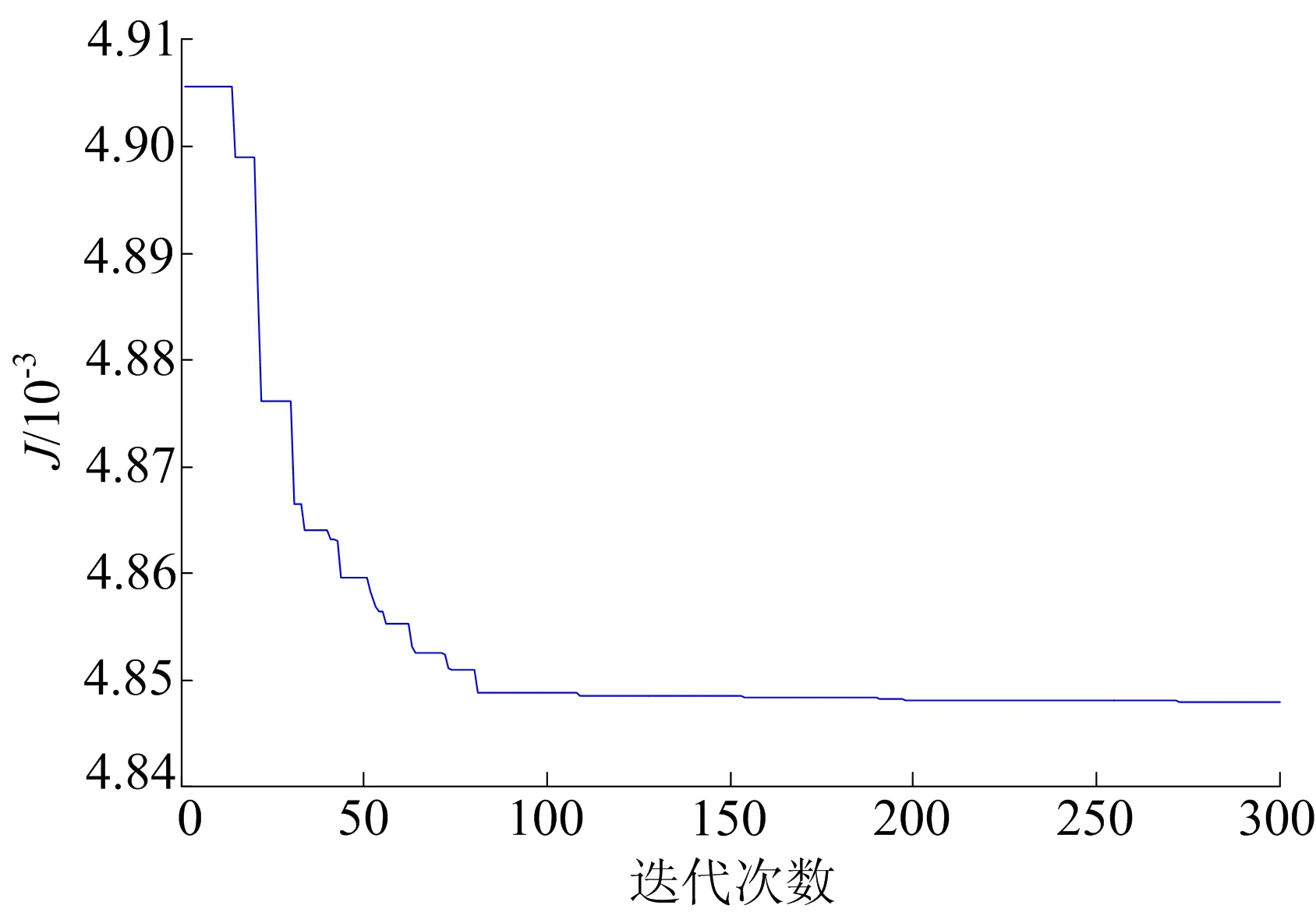
图5 函数最优解随迭代变化

由图4可知,相对于传统PID控制,ICSO-FUZZY-PID控制的超调量更小、静态误差更小、动态响应速度更快。通过Matlab中编写的程序,得到传统PID控制下的ITAE指标为0.026 8,ICSO-FUZZY-PID控制下的ITAE指标为0.004 847,后者约为前者的18.3%。优化后的Ke=0.499 96、Kec=0.519 24、Kp=0.014 034、Ki=5.224 1、Kd=4.999。由图5可知,系统在迭代到约75次时,函数最优解趋向于平稳。

为检验系统自适应性能,在0.5 s后给输入端突加一个幅值为5 mm的阶跃扰动,仿真结果如图6所示。

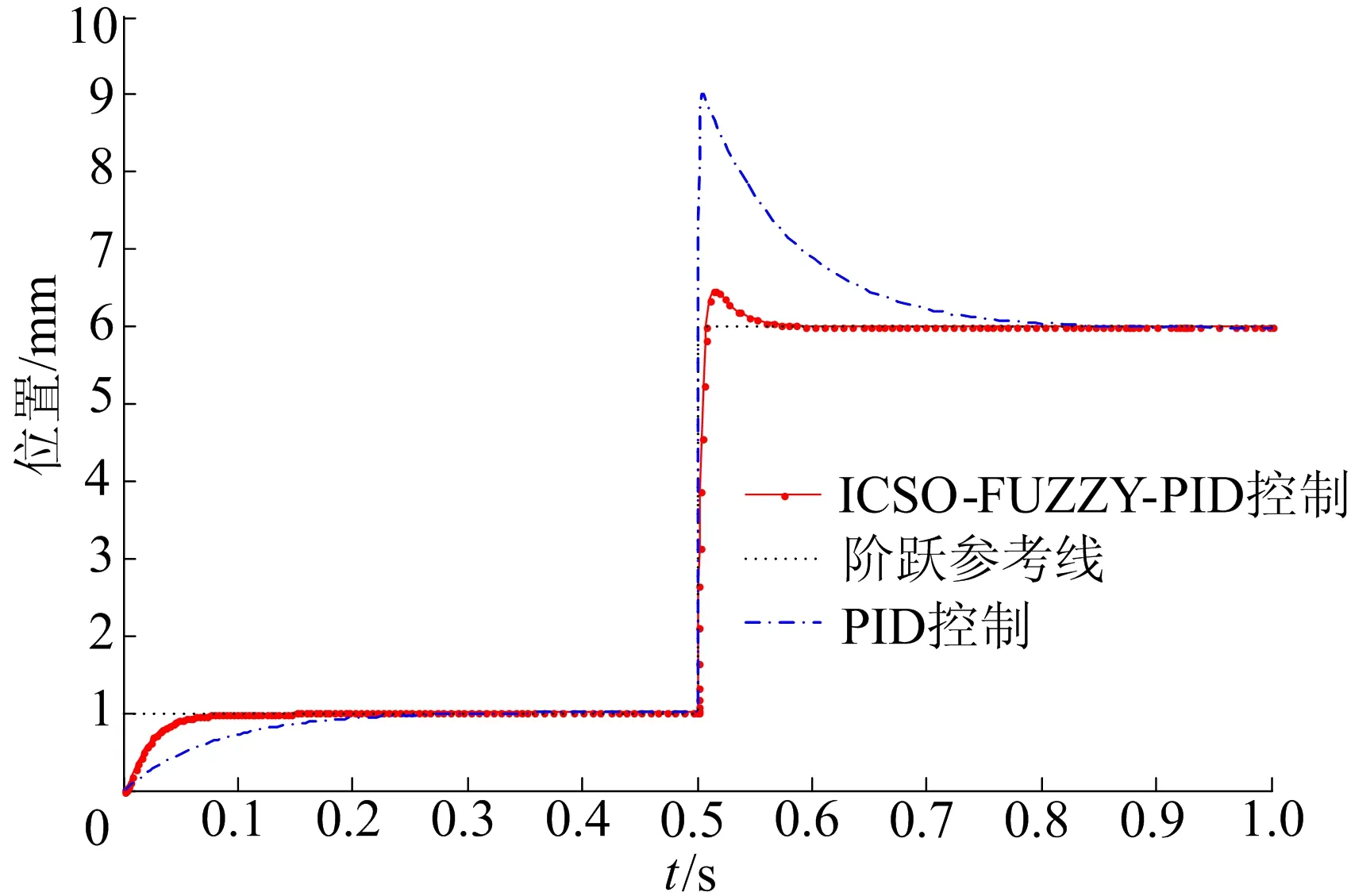
图6 0.5 s突加阶跃扰动时2种控制方法的位置控制仿真比较

从图6可以看出,系统的输入发生较大变化后,ICSO-FUZZY-PID控制下的跟踪响应与调节性能比传统PID控制下具有更好的自适应性能、更强的鲁棒性以及更优的跟踪性能。通过Matlab编写的程序得到传统PID控制下的ITAE指标为0.187 48,ICSO-FUZZY-PID控制下的ITAE指标为0.018 782,后者约为前者的10%。优化后的Ke=0.045 233、Kec=0.659 45、Kp=0.012 11、Ki=10.080 4、Kd=4.955。

4.2 实验验证

为验证本文设计的ICSO-FUZZY-PID位置控制器的控制性能,在已有的PMLSM系统实验平台上进行实验验证。平台的运动控制系统主要由直线电机运动平台和运动控制卡组成。采用美国Delta Tau公司的Turbo PMAC运动控制卡,型号为Turbo PMAC2 Clipper,运动控制卡主要负责系统数据采集、信号处理及控制等;驱动器采用以色列MEGA-FABS公司生产的D1型MD-36-S;X轴PMLSM来自台湾HIWIN,型号为LMCB6,行程为750 mm;采用雷尼绍公司型号为RGH22Y、分辨率为0.1 μm的直线光栅作为运动反馈部件,采集实际运动位置信号并反馈给运动控制卡,从而构成全闭环控制。实验平台如图7所示。

图7 实验平台

利用PMAC运动控制卡所具有的开放伺服特性,编译出采用改进CSO算法优化后的模糊PID控制的直线电机伺服算法程序,具体的实验验证如下所述。

在空载情况下,实验平台的位置环先后采取传统PID控制策略及本文提出的ICSO-FUZZY-PID控制策略,进行步长为100 μm、步长时间为500 ms的阶跃运动,实验结果如图8所示。其中跟踪误差e的单位为μm，下文同。

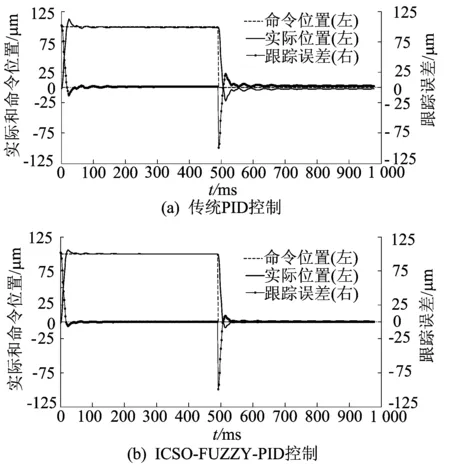
图8 2种不同控制策略下的阶跃运动实验结果

由图8可知,给定阶跃信号时,传统PID控制下跟踪误差e在[-15.6,15.6]范围内,ICSO-FUZZY-PID控制下跟踪误差e在[-7.2,7.2]范围内,后者约为前者的46.2%。结果表明,本文ICSO-FUZZY-PID控制策略相比于实验平台原本采用的传统PID控制策略,可以获得更好的动、静态特性,其控制效果得到了明显改善。

为验证本文方法的自适应性能和跟踪性能,本文进行2组对比实验。

(1) 第1组实验。在X轴上加上150 N的负载阻力,实验平台的位置环先、后采取传统PID控制策略和本文ICSO-FUZZY-PID控制策略,选择与上述阶跃运动相同的起始位置处进行相同的阶跃运动实验,以便尽量减小实验误差。实验结果如图9所示。

由图8、图9对比分析可知,在施加150 N负载阻力的情况下,传统PID控制下跟踪误差e在[-22.0,12.6]范围内,ICSO-FUZZY-PID控制下跟踪误差e在[-8.6,6.1]范围内,后者约为前者的42.5%。结果表明,常规的PID控制自适应能力较差,系统的稳定性较差;而ICSO-FUZZY-PID控制下直线电机伺服系统能随着外部环境的变化作出自适应调整,具有良好的自适应性能和跟踪性能。

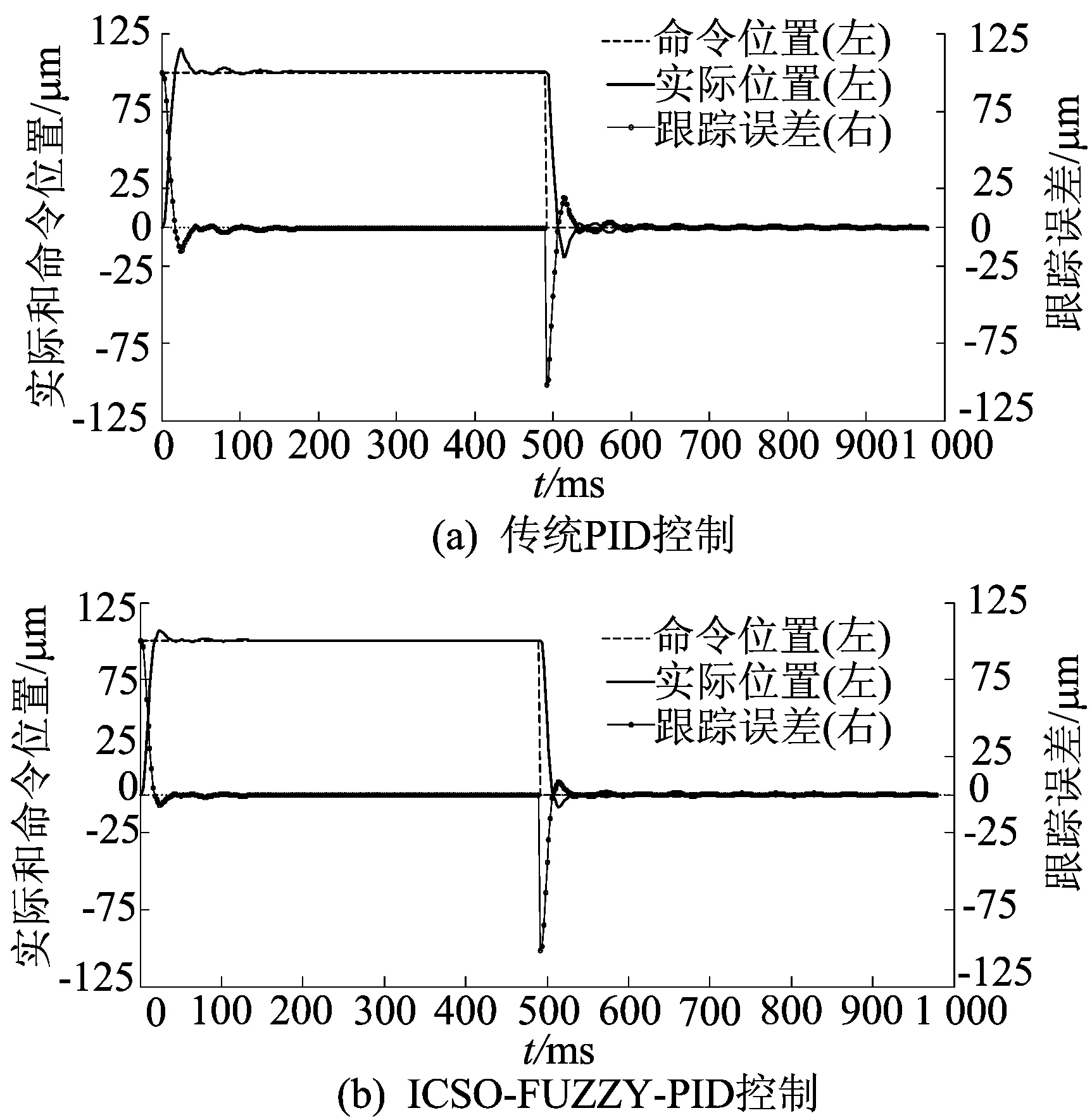
图9 2种不同控制策略下带150 N负载的阶跃运动实验结果

(2) 第2组实验。在空载情况下,实验平台的位置环先、后采取传统PID控制策略和本文ICSO-FUZZY-PID控制策略,进行f(t)=1 000sin(2πt)正弦运动,实验结果如图10所示。

由图10可知,给定正弦信号时,传统PID控制下跟踪误差e在[-4.5,3.4]范围内,ICSO-FUZZY-PID控制下跟踪误差e在[-1.8,1.8]范围内,后者约为前者的45.6%。因此,相比于传统PID控制策略,本文ICSO-FUZZY-PID控制策略具备更好的自适应性和跟踪性能。

5 结 论

本文对PMLSM数学模型进行了分析,根据系统性能需要,提出了模糊PID控制器与ICSO算法相结合的控制方法,并应用于PMLSM伺服系统位置环。结果表明, ICSO优化模糊PID的控制策略比传统PID控制策略具有更好的控制性能和更优的动、静态特性。