平面扭转式强磁场测量微传感器的设计与分析

王月媖, 许高斌,2, 王超超, 陈 兴, 马渊明

(1.合肥工业大学 电子科学与应用物理学院,安徽 合肥 230601; 2.安徽省微电子机械系统工程技术研究中心,安徽 合肥 230601)

由于人类发展对能源的不断需求,基于更安全的磁约束聚变的托卡马克装置越来越被重视[1-3]。托卡马克装置内部由多种“D”字型磁体线圈产生的约束磁场约束高温的带电粒子在其中做高速旋转的拉莫运动,再附加其他辅助加热手段,使等离子加热到一定温度,发生聚变反应。等离子运动产生的感生磁场还会随着电流的变化而变化,使得托卡马克装置内部成为一个复杂的高温强辐射的电磁环境[4]。为了更有效地控制托卡马克,减少其不可控性对人类造成的危害,需要了解托卡马克内部磁场大小、方向及分布,微机电系统(Micro-Electro-Mechanical System,MEMS)传感器以其小型化、高性能和独立可控性成为首选[5-7]。

随着微电子产业的兴起,微传感器发展迅速,但用于T量级的强磁场测量传感器极少。文献[8-11]利用磁性材料的巨磁阻抗效应(giant magneto-impedance,GMI)[12]研究、设计、优化的GMI磁传感器弥补了传统磁传感器的不足,具有高稳定性、高灵敏度、高分辨率、响应速度快及功耗低的特点[13],但测量范围未涉及托卡马克内部测量所需磁场量级;文献[14]针对肿瘤热疗发生装置中产生的中频强磁场,设计了一种通过测量空间三坐标磁场分量再合成磁场矢量的三维传感器,但其测量范围最高只能达到0.03 T,远远不能满足托卡马克内部强磁要求。

本文针对托卡马克复杂的内部环境,设计了电容检出式平面扭转MEMS传感器结构[15],选用耐高温、抗强辐射的材料,以克服托卡马克内部恶劣环境的干扰。该传感器测量范围为0.05 ～1.50 T。

1 结构设计与理论建模

平面扭转式微传感器是以绝缘层上的硅(silicon-on-insulator,SOI)晶片为原材料制备的、横截面为8字型外框形状的传感器。在其横截面“腰”间两侧分别制备1根以Y方向为长度方向的扭转梁,并分别固定在两边的锚区,从而支撑悬空的扭转平面;金属线圈由引入电极接入,沿扭转平面外侧从外到内等间距环绕,并通过隔离层接到引出电极上;中心电极与其下直达电容上极板的通孔内的填充金属相连,使中心电极与电容上极板保持电学连通,并通过隔离层与第2电容电极相连;第1电容电极通过其下通孔内的填充金属与电容下极板保持电学连通。平面扭转式微传感器结构的主体部分从上到下分别为银材料金属线圈、氧化硅层、硅层、氧化硅层、铜材料电容上极板层。

为提高结构的性能参数,本文选用不同尺寸参数进行优化设计。为叙述方便,称初始结构为结构1。用于测量X、Y方向磁场分量的平面扭转式微传感器结构1工作原理如图1所示。

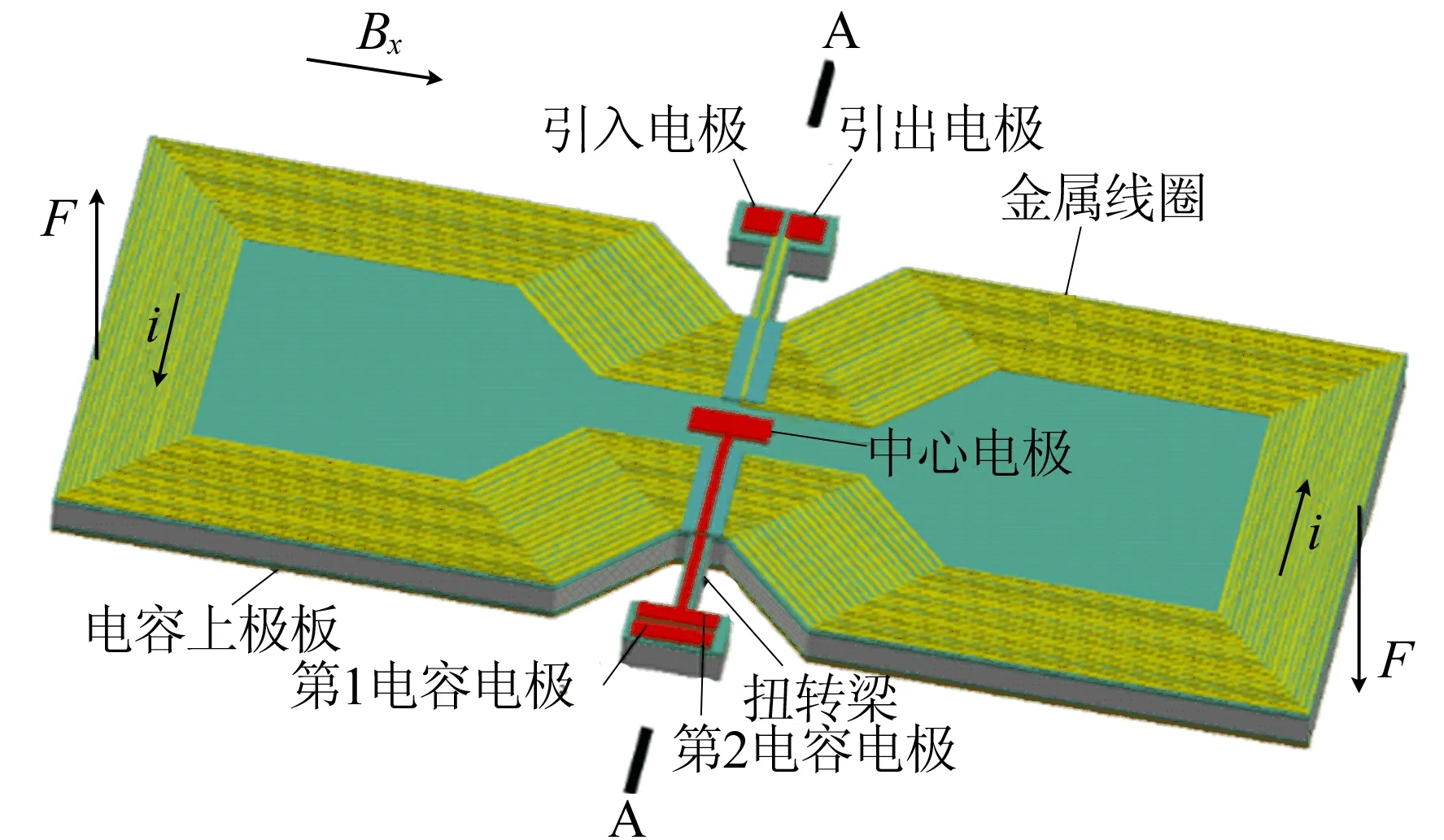
(a) X方向结构

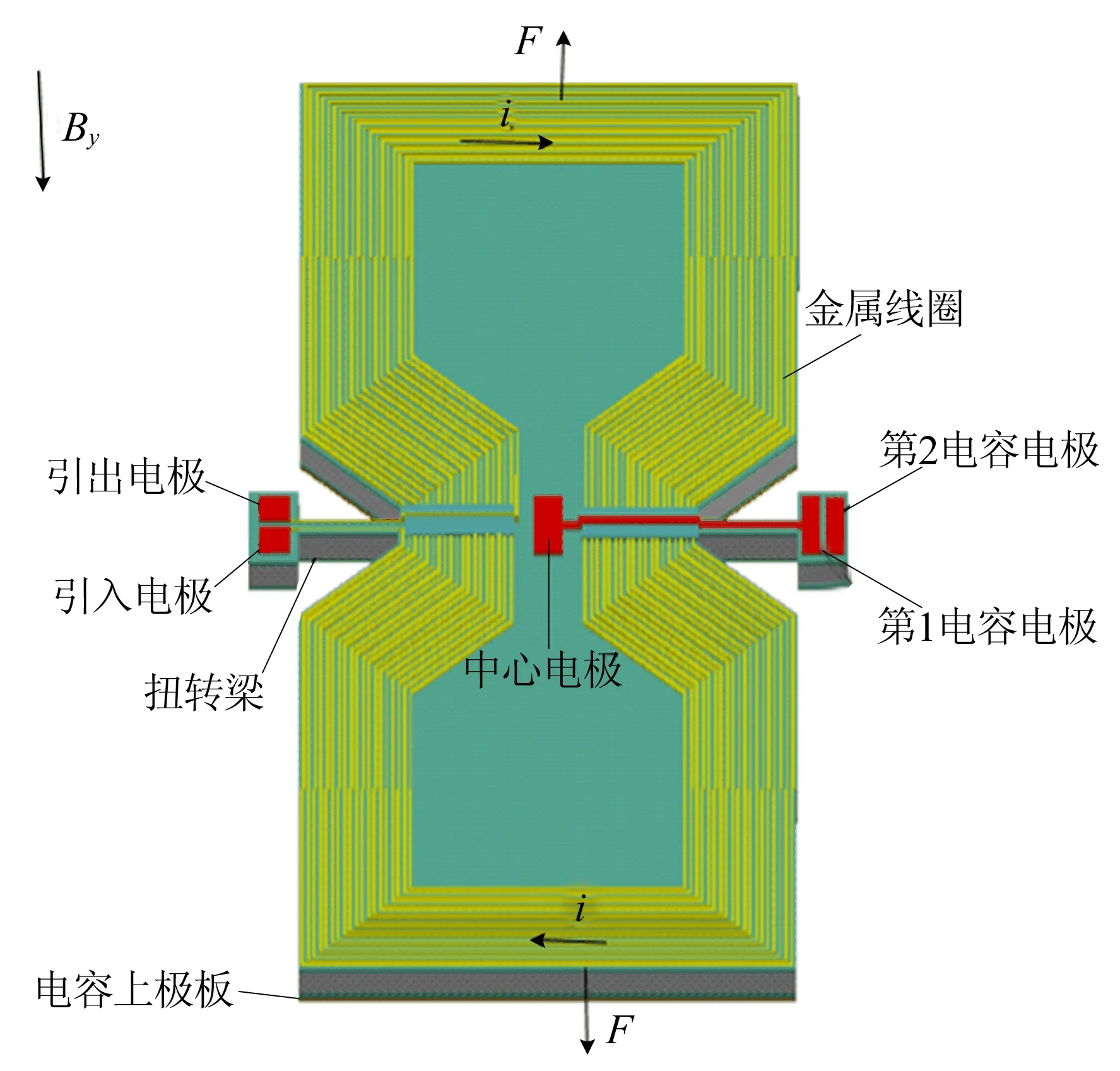
(b) Y方向结构图1 平面扭转式微传感器结构1示意图

存在X、Y方向磁场的情况下,通入交流信号的金属线圈会受到洛伦兹力F和磁力矩T,其大小分别为:

F=iclB

(1)

T=icSBsinα

(2)

其中,ic为金属线圈上的电流;B为磁感应强度;l为与磁场B垂直的受洛伦兹力的金属线圈的有效长度;S为金属线圈的环路面积;α为金属线圈所在平面与磁场B的夹角。F和T的方向分别通过左手定则和右手定则来判断。

平板受力扭转的扭转角[16]为:

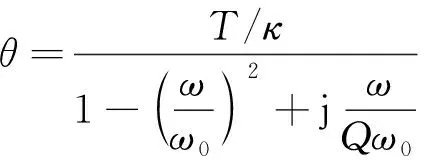
(3)

其中,θ为平板的扭转角;κ为结构扭转梁的弹性系数;ω为平板振动时的角频率;ω0为谐振角频率;Q为品质因数,是结构设计中的一个重要参数,是储存能量与损耗能量之比的一个质量指标。ω0、Q的计算公式分别为:

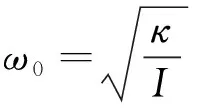
(4)

(5)

其中,I为转动惯量;γ为周围空气对结构所产生阻尼的阻尼系数,计算公式[17]为:

γ=αM+βK

(6)

其中,M为质量矩阵;K为刚度矩阵;α、β分别为质量比例阻尼系数和刚度比例阻尼系数。

线圈输入的是交变电流,假设输入幅值为1 A的正弦电流,则外扭矩T也呈正弦函数变化趋势,(3)式可改为:

(7)

(8)

其中,ε0为极板间介质的介电常数。

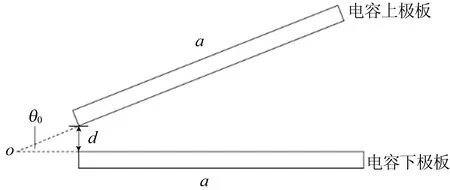
图2 非平行平板电容器原理

理论上,建立磁场B与电容C之间的关系式为:

(9)

因此,通过测量变化的C值即可推导出所处环境下磁场B的大小。

ZC、ZL计算公式为:

(10)

ZL=2πfL

(11)

(12)

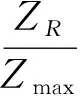
2 模拟分析与验证

针对不同尺寸下的平面扭转式微传感器结构,分别通过ANSYS有限元仿真软件Ansoft Maxwell、ANSYS Workbench对结构的谐振频率f0、品质因数Q、分辨率进行计算。

结构1尺寸如下:腰角度为45°,线圈匝数为20,线圈宽度为3 μm,线圈间距为3 μm,梁长100 μm。对模拟得到的电场E、磁场B和电势V分布云图进行分析,线圈通电后产生磁场,在传感器实际测量过程中要考虑线圈通电自身产生的磁场对结果数据的影响。磁场随通入电流的变化而变化,变化的磁场产生电场。绕线线圈内磁通量的变化,线圈上会产生感应电势,磁通量变化越快,电势越高,对电容极板加电压计算电容影响越大,因此应尽量降低传感器的f0。

在0.30 T下ZC、ZL随频率f变化的曲线如图3所示。

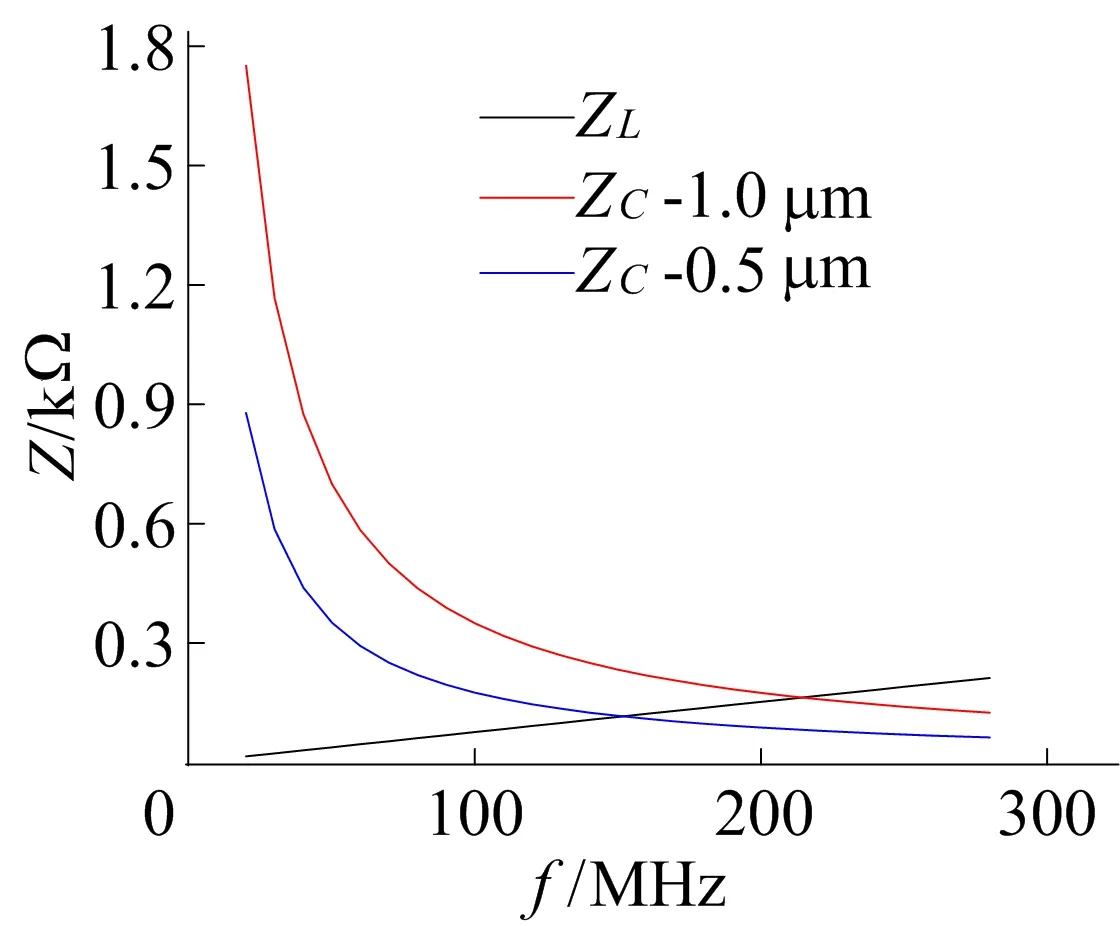
图3 0.30 T下ZC、ZL随f变化曲线

从图3可以看出,电容间距为1.0、0.5 μm下ZC随f的整体变化趋势相同,在较低f值下两者相差较大,f越大,2种电容间距下的ZC相差越小,并趋于相同。

当ZL与ZC相同时,该传感器结构的平板扭转振幅达到最大,此时,传感器会发生谐振,与通过(7)式计算得到的f0值相同,即在0.30 T下电容间距为0.5 μm时的f0为151 MHz,电容间距为1.0 μm时的f0为214 MHz。

2种电容间距下的ZR/Zmax-f曲线如图4所示。

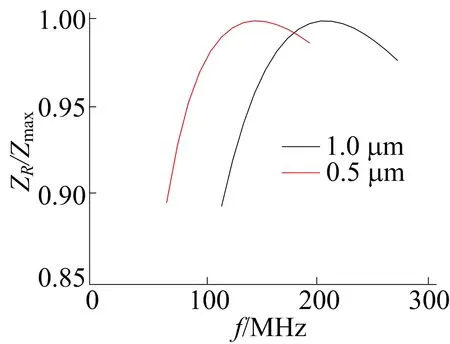
图4 0.30 T下2种电容间距下ZR/Zmax-f变化曲线

0.30、0.35 T下2种电容间距下结构1的f0、Q值见表1所列。

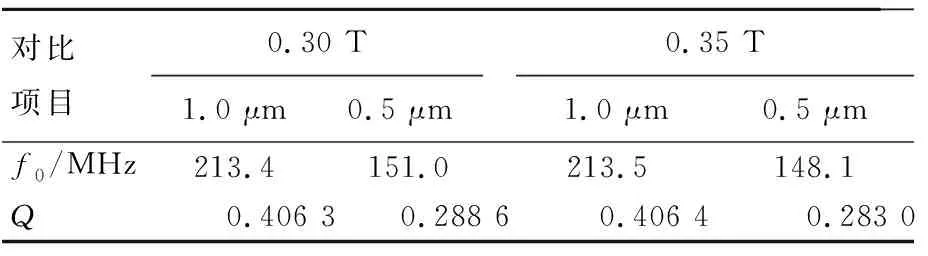
表1 0.30、0.35 T下不同电容间距结构1的f0、Q值

传感器在0.35 T磁场作用下,电容间距为1.0 μm时ZC为4.526 2 pF，0.5 μm时ZC为9.053 1 pF;在0.30 T磁场作用下,电容间距为1.0、0.5 μm时的ZC分别为4.544 8、9.058 2 pF。根据表1和计算分析可知,2种磁场值下的ZC有明显变化,而f0值变化很小。

对于电容间距为1.0 μm的电容,磁场变化0.05 T时,分辨率为0.058 pF/T; 对于电容间距为0.5 μm的电容,磁场变化0.05 T时,分辨率明显增大到7.224 pF/T。0.5 μm电容间距下的分辨率明显比1.0 μm电容间距下的的分辨率大。

1.0 μm电容间距的传感器结构在0.30、0.35 T下的Q值差别不大,说明磁场变化远没有传感器结构尺寸参数变化对其Q值的影响大。

减少电容间距能有效降低f0,分辨率也大幅度提高,但是电容间距减小,使得不必要的、应当尽量避免的耦合电容增大,损耗的能量增大,Q值减小,因此选择合适的电容间距十分重要。

因此,为提高结构的性能参数,需要进行优化设计。13种结构的不同尺寸参数见表2所列。对13种结构进行仿真计算,结果见表3、表4所列。

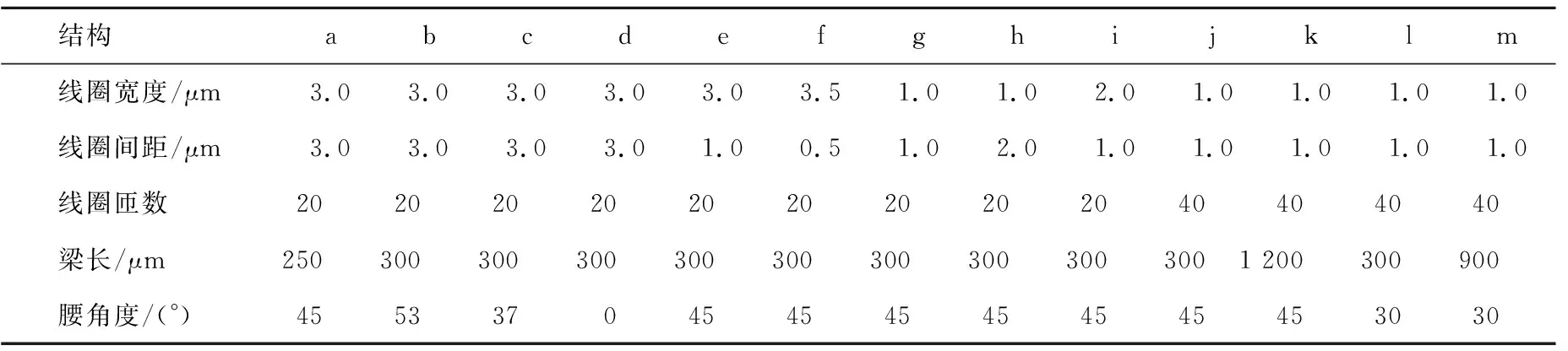
表2 13种结构的尺寸参数

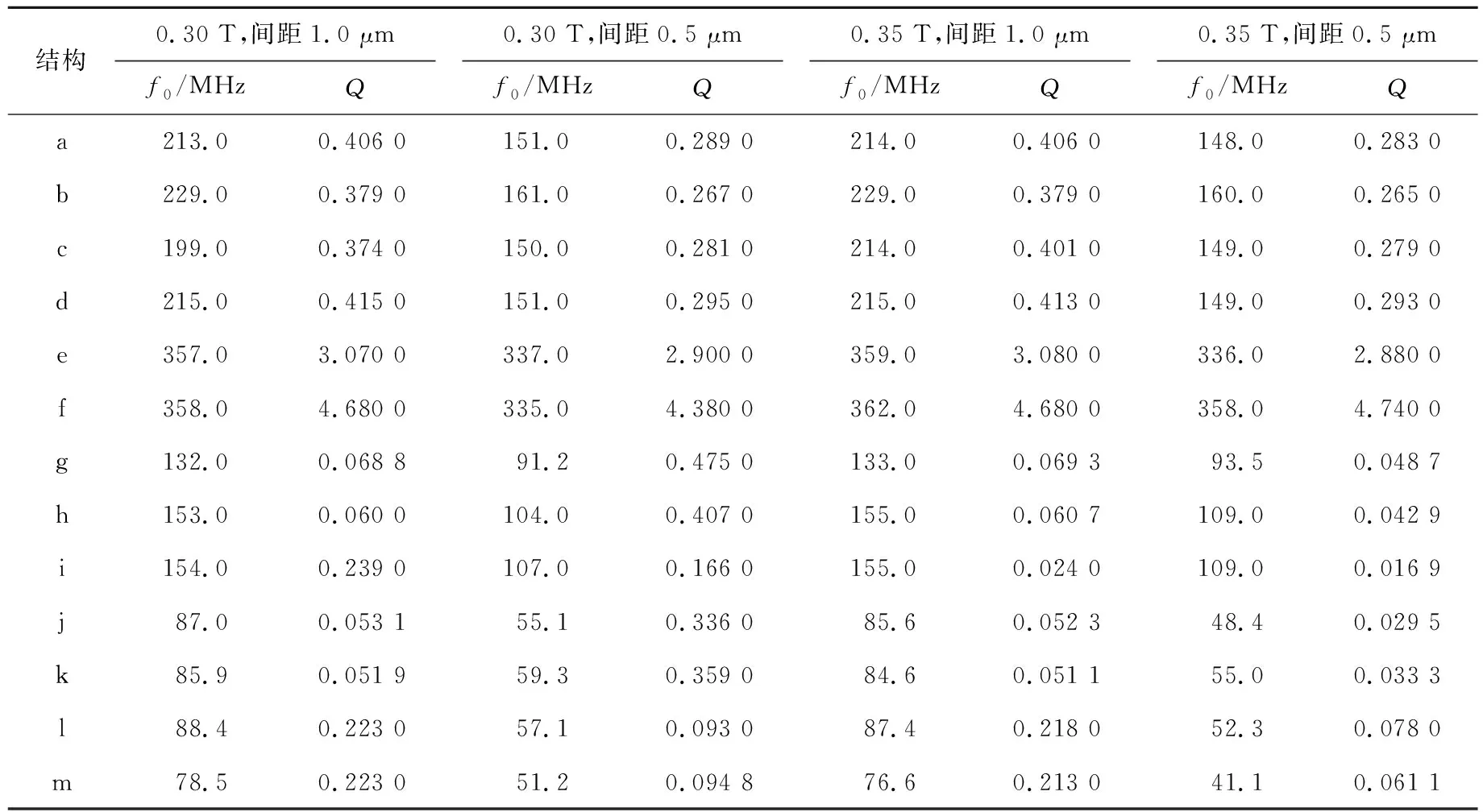
表3 0.30、0.35 T下2种电容间距下13种结构的f0、Q值

表4 磁场从0.3 T变化到 0.35 T时13种结构在初始间距为1.0、0.5 μm下的分辨率 pF/T

从分辨率角度看,不同尺寸下的结构有以下特点:

(1) 在电容间距1.0 μm时,结构c的分辨率较高,而结构d的分辨率较低,由此可知腰角度对分辨率有较大影响,但角度太小反而会使得分辨率变小,因此存在一个最优角度值。

(2) 在电容间距为0.5 μm时,结构j～结构m的分辨率明显比其他结构的大,这说明在小电容间距下,线圈匝数对分辨率的影响最大,线圈匝数越大,结构的分辨率越大。

(3) 梁长对分辨率的影响较大。在电容间距为0.5 μm时,比较结构l和结构m的分辨率值可知,梁长越大分辨率越高;比较结构j和结构k的分辨率值可知,梁长越大分辨率越低。因此,存在一个最优的梁长值,不能无限制地增加梁长来强迫提高结构性能参数。

从f0角度看,结构j～结构m的f0相比于其他结构有明显降低,说明线圈匝数对于降低结构的f0有非常明显的作用,且匝数越多,f0越低。

3 结 论

本文设计了一种平面扭转式微传感器,其测量范围在0.05 ～1.50 T,当线圈通入交变电流后,在外部磁场作用下产生洛伦兹力,驱动平板周期性扭转,再通过测量电容变化量反推磁场大小;分析了传感器的工作原理,对结构设计进行综合考虑,给出不同尺寸参数下的传感器结构。通过仿真计算发现,不同尺寸结构的性能参数在2种磁场B值下差异较大,其中,结构m在0.35 T下电容间距为0.5 μm时,谐振频率可达41.1 MHz，分辨率可达122.860 pF/T。

本文设计研究的MEMS强磁传感器可为目前先进超导托卡马克实验装置(Experimental Advanced Superconducting Tokamak,EAST)磁场测量提供校准参考,以消除电磁感应线圈长期的漂移误差,并进一步为超导托卡马克装置未来千秒长脉冲准稳态磁场测量诊断系统提供相关解决方案和技术积累。