基于k段主曲线的山区GPS轨迹融合算法研究

曹奇林, 徐本柱

(合肥工业大学 计算机与信息学院,安徽 合肥 230601)

近些年来,随着地理信息系统(geographic information system,GIS)技术的应用普及,数字地图的使用越来越广泛,基于高精度数字地图的定位越来越重要。由于山区全球定位系统(Global Positioning System,GPS)信号较弱,道路信息相比于城市路网不那么完善,对于精确数字地图的需求就大大增加。

主曲线是第一线性主成分的一般化,由Hastie和Stuetzle于20世纪80年代提出,其目标是使用一条光滑曲线来近似描述数据集[1]。现有的主曲线算法对于提取分散度大、高度弯曲及自相交等复杂形态数据,效果不理想[2]。文献[3]提出一种k段主曲线算法来提取主曲线,解决了该类问题。在轨迹融合方面,文献[4]针对大量的铁路轨道GPS定位数据,提出采用非线性组合数据约简模型来减少存储空间,并利用二分法的思想提出3种算法,使得铁路轨道数字地图的获取更简单;文献[5]提出了3种带约束的主曲线算法,对于铁道轨迹数据可以得到理想结果;文献[6]研究了多铁道轨迹信息融合问题,提出改进的融合算法,但是算法过程较为复杂,实用性较差;文献[7]提出了一种曲线线路的表示方法,采用连续的线段近似表示铁路轨道中的曲线形状部分;文献[8]提出要充分利用线路中存在的固定点,并给出了算法和模型,但是算法比较复杂,实用性差;文献[9]研究了车辆的无线定位,为了提高定位的精度,提出使用轨迹融合的方法,并且进行了相关验证试验。

文献[10]提出了3种面向铁路轨迹信息的融合算法,分别是CPCLa、CPCLs及CPCLi。其中,CPCLa算法主要思想是通过不断增加顶点最终得到一条满足误差要求的k段主曲线;CPCLs算法和CPCLi算法对CPCLa算法进行了改进,主要是利用一维搜索的方法和进一步优化搜索空间的选择。由于山区的复杂地理环境会对GPS信号产生影响,信号太弱时,GPS接收机可能无法定位,而信号太强时,也会对定位产生干扰,从而产生漂移现象[11],即出现与实际位置不符的情况。同时由于山区路况复杂,采集到的GPS轨迹数据在部分区域具有数据分布稀疏且不均匀的特点,或者数据中包含离群值,而现有的融合算法对于山区GPS轨迹数据的融合问题处理效果不佳。

针对此问题,本文首先介绍文献[10]中的算法模型,然后对其进行优化,提出一种改进的GPS轨迹融合算法,最后通过实测山区轨迹数据进行验证。本文算法可以有效融合低精度GPS数据,且计算效率高,节省了人力和成本,适用范围更大。

1 问题建模

1.1 问题描述

因为一些山体的干扰、人为因素的影响等等,在山区采集的原始数据中会有很多的噪音数据,无法直接使用,所以对其进行融合处理,最终结果采用折线段来描述实际曲线,即采样点云的骨架。

本文研究的问题描述如图1所示。

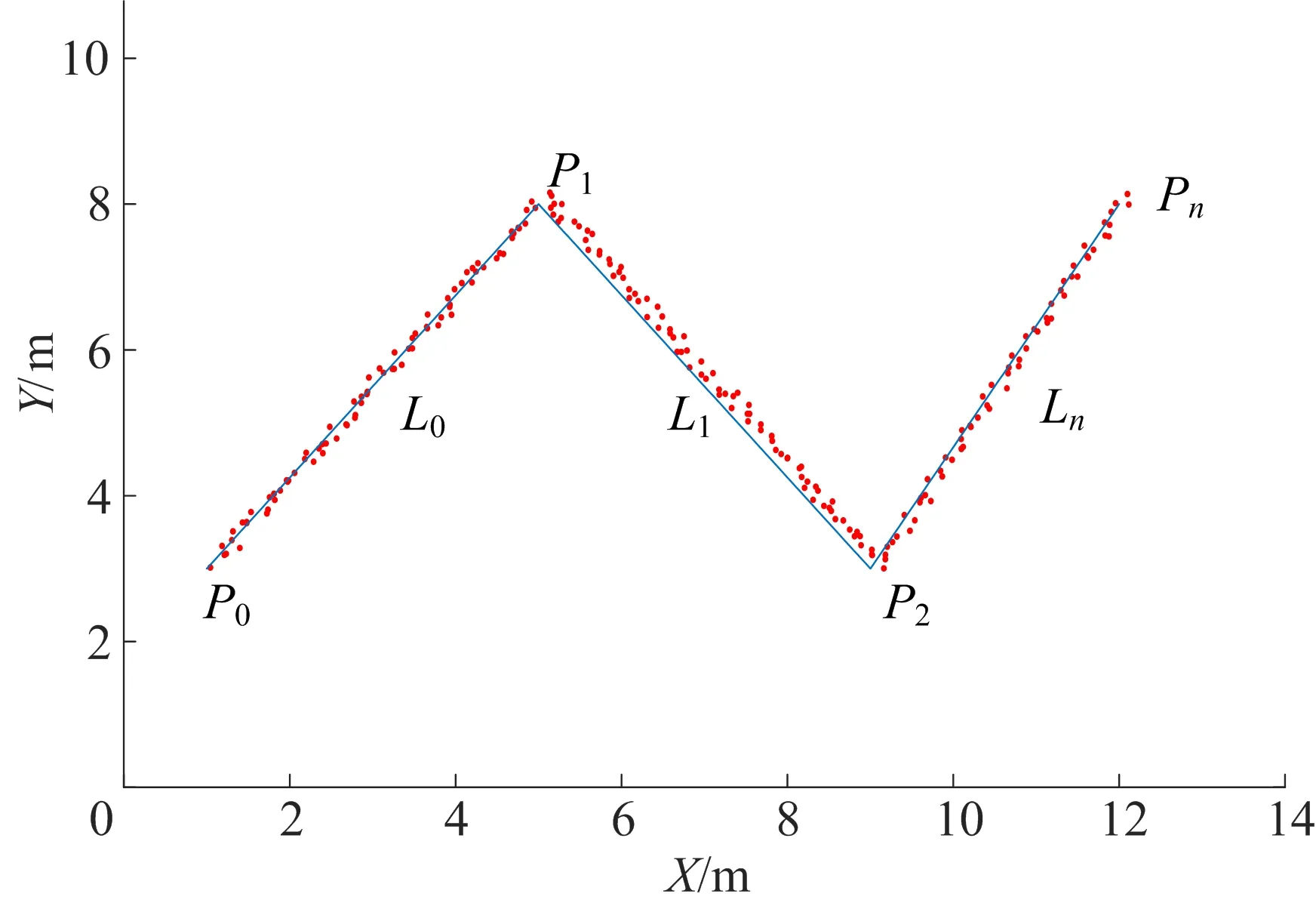
图1 问题描述

设顶点为Pi(i=1,2,…,n),数据点为dj(j=1,2,…,s),Li表示以Pi、Pi+1两点作为端点构成的线段。

k段主曲线是包含一系列通过数据集“中央”的线段的曲线,一般地,k段主曲线通过从初始主成分分析(principal component analysis, PCA)解逐步添加顶点,并且最小化点到线段和顶点之间距离得到。而约束k段主曲线的目标是利用最近邻原则在固定端点的前提下生成k段主曲线。根据最近邻原则,所有的数据点都被划分到对应的线段和顶点。采取的原则是首先计算每个数据点与主曲线的各个顶点以及所有线段的距离,然后比较这些距离值,最小的距离值对应的顶点或者线段就是该数据点的所属区域。

1.2 数学模型

根据最近邻原则需要得到数据点dj到对应线段Li的距离为:

DLi,j=[|(XPi+1-XPi)Ydj-(YPi+1-

YPi)Xdj+XPiYPi+1-XPi+1YPi|]/

[(XPi+1-XPi)2+(YPi+1-YPi)2]1/2

(1)

数据点dj到对应顶点Pi的距离为:

(2)

其中,Xdj、Ydj为数据点dj的X、Y轴坐标;XPi、YPi、XPi+1、YPi+1分别为顶点Pi、Pi+1的X、Y轴坐标。

将数据点到目标折线段上最近的顶点或线段的垂直距离定义为投影距离,假设线段Lv的顶点为Pv和Pv+1,相邻数据点为tj′(j′=p,p+1,…,q),则线段Lv相邻数据点的平均投影距离AD定义为:

(3)

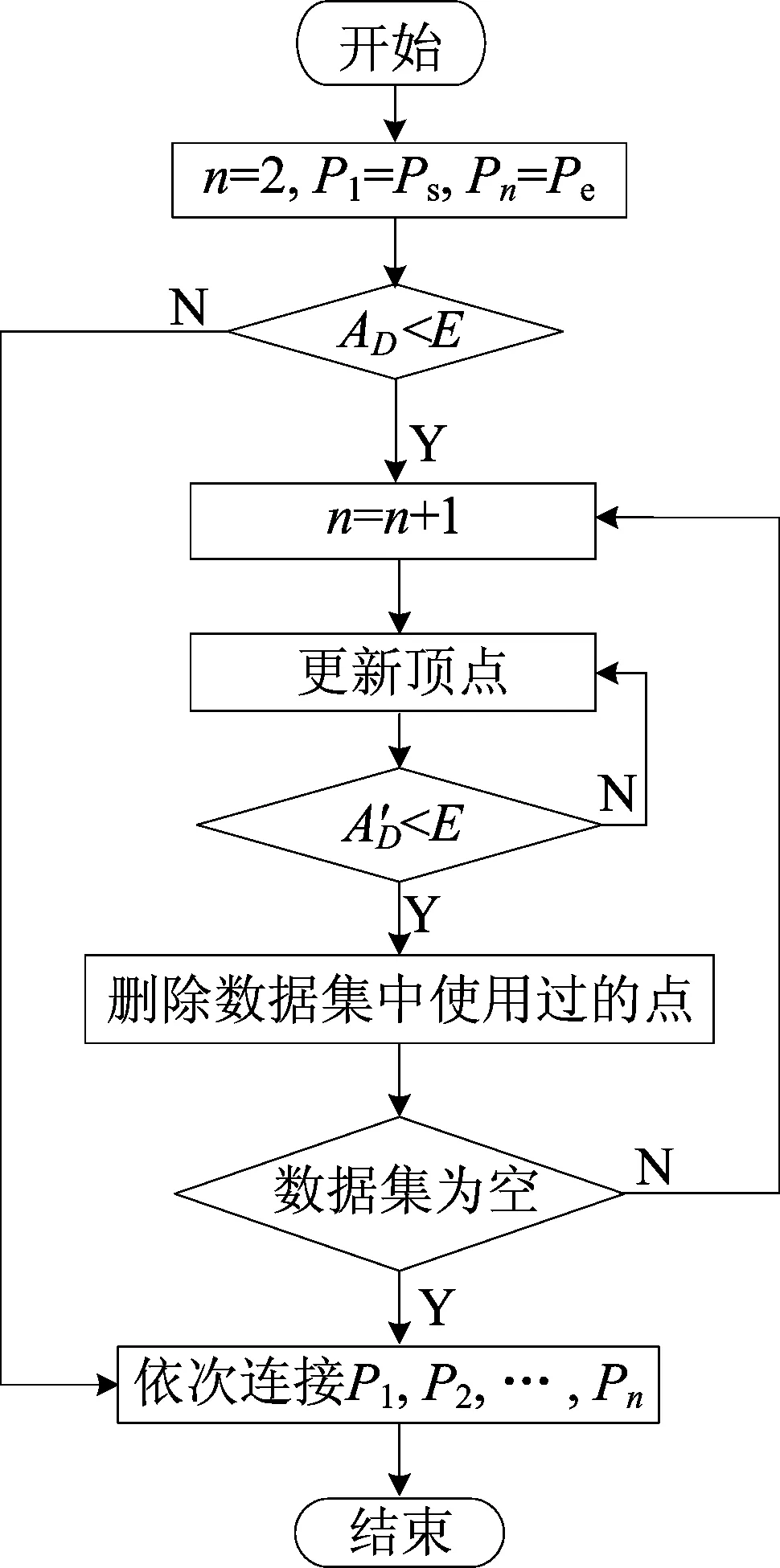
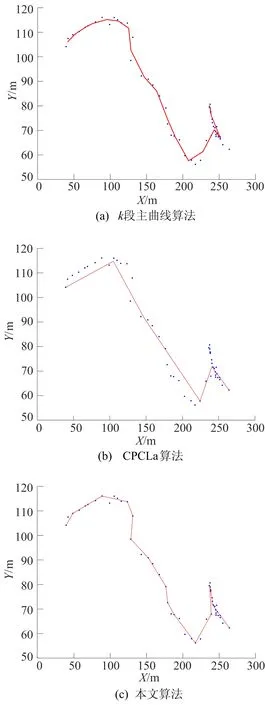
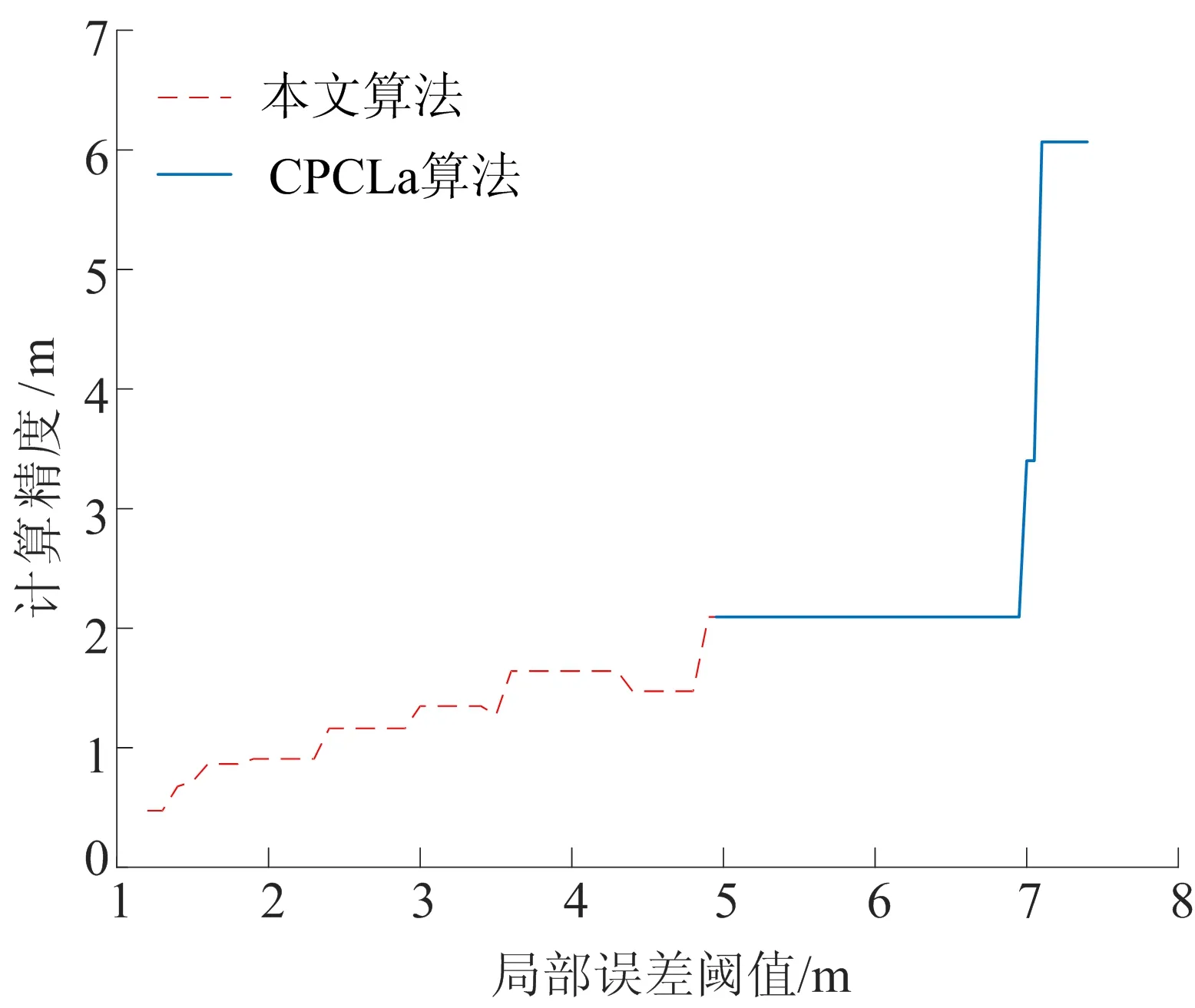
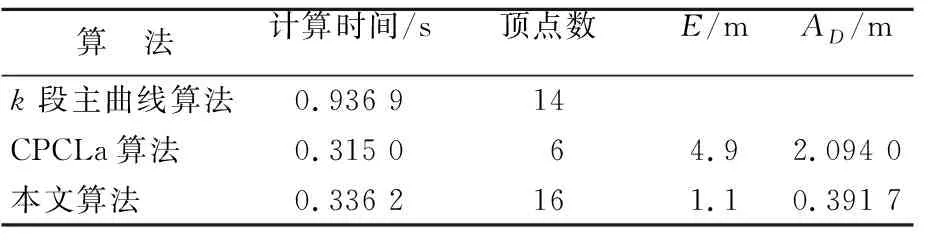
约束条件为:AD

局部误差阈值E的设置与数据有关,E太小则有可能无法构造主曲线,需要根据经验判断,数据分布比较均匀时,E取值较小;否则E一般取值稍大。

2 基于主曲线的自适应融合算法

本文算法首先对GPS数据进行坐标系转换,将经纬度转换成为适合处理的平面坐标。由于采集到的GPS轨迹数据分布不均匀,无法直接处理,因此需要对其进行预处理,清除由于采集数据时GPS手持机发生略微抖动或者微小位移产生的冗余数据和漂移点。具体算法步骤如下。

初始化:n=2,n表示顶点个数。P1=Ps,Pn=Pe,其中Ps、Pe分别为起点和终点。

(1) 连接Pn-1和Pn作为初始子主曲线Ln-1。

(2) 计算所有未使用过数据点到线段Ln-1的平均投影距离AD是否小于预设误差阈值E,若满足条件则进入步骤(4),否则进入步骤(3)。

(3)n=n+1,增加新顶点Pn-1,连接Pn-2、Pn-1构成子主曲线,计算线段Ln-2的局部误差AD′,判断AD′是否小于E,若满足,则从数据集中删除使用过的数据点,同时以Pn-1为起点,继续增加新顶点,直至数据集为空;若不满足则更新顶点,得到新顶点Pn-1′,重复此步骤。

(4) 将各个顶点P1,…,Pn依次连接得到最终结果,即k段主曲线生成结束。

其中,步骤(3)中添加新顶点以及更新顶点的方式是:以Pn-2为圆心,所有未使用过的数据点dt(t=1,2,…,m)到圆心的距离最大值为半径R画圆,同时以R′=Rθ(θ此处取值为0.8)为半径画另一个圆,取落在圆环中的m′个数据点坐标的平均值作为新顶点的可能取值。

本文在构造主曲线的过程中,对更新顶点步骤进行改进,考虑到山区GPS采集数据特点,当m′不为0时,将半径缩小为原来的1/2,即R=R/2;当m′为0时,即无法根据所画圆环获得顶点的坐标,为了能够顺利构造主曲线,将在区间[R,2R]中继续寻找顶点,即R=R+R/2n,直到找到满足误差要求的顶点坐标。算法流程如图2所示。

图2 算法流程

3 实验结果与分析

本文采用的实验环境为Matlab R2016a, CPU为Intel(R) Core(TM) i5-4590(3.30 GHz),内存4.00 GiB,Windows10操作系统。实验数据是由黄山风景区索道管理人员采用手持GPS接收机人工采集,GPS手持机型号为GPSMAP 60CS,误差范围为15 m。

所采集的区域包括整个黄山风景区各个游览路段的GPS数据信息。为了验证本文算法对于复杂形状路径信息融合的可行性与适应度,选取黄山风景区鳌鱼峰南北路口之间的一段路径信息作为实验对象,将采集到的51个轨迹点作为算法输入,采用本文算法、文献[10]中CPCLa算法及k段主曲线算法对该路段进行轨迹融合,最终结果如图3所示。

图3 3种算法生成结果

局部误差阈值与算法精度之间的变化关系如图4所示。

图4 本文算法与CPCLa算法误差变化曲线

2种算法的性能对比见表1所列。

表1 算法性能误差比较

由图3、图4及表1可以看出:①k段主曲线算法由于涉及角度惩罚参数设置、没有约束点和局部误差阈值的概念,因此无法与另2种算法比较E和AD,且运算时间最长;② CPCLa算法对于复杂数据的适应性不好,对于预设误差阈值的依赖度较高,由于没有考虑数据分布分散的情况,得到的结果AD较大,而且与实际位置偏差较大,虽然顶点数较少(即节省了存储空间),但是损失了计算精度;③ 本文算法可以提取符合实际曲线的处理结果,缩短轨迹生成时间,而且精度最高,占用内存空间较小,适应性更强;④ CPCLa算法和本文算法的运算时间都较少,本文算法由于对CPCLa算法的顶点更新步骤进行了改进,因此本文算法可以获得更高精度的结果。

经过多次验证实验,在不同复杂度的样本数据下,本文算法测试结果均表现良好,可以快速生成GPS轨迹融合结果,满足高精度数字地图的要求。

4 结 论

本文在主曲线思想的基础上,采用已有的模型算法对山区GPS轨迹数据融合作了深入研究,提出一种改进的融合算法,适用范围广,算法性能较好;通过黄山风景区实测的GPS数据对算法进行验证,实验结果表明本文算法计算时间较少,占用存储空间少,生成结果符合实际数据曲线,具有一定的现实意义。

后续研究将在目前所获得的解的基础上进行优化,同时考虑相邻线段之间的转角对于生成轨迹结果的影响,使算法性能进一步提升,提高算法的鲁棒性和计算精度等。