多相流气液边界处理

韦 建, 朱晓临, 张义群

(合肥工业大学 数学学院,安徽 合肥 230601)

关于多相流动,文献[1]认为根据固体、液体、气体中的任何两相组合或三相组合,可以分为气液两相流、液液两相流、气固两相流、固液两相流、气液固三相流等。近年来,气液两相流动数值模拟技术是计算流体动力学(computational fluid dynamics,CFD)领域研究的热点和前沿课题之一。在图形图像模拟方面,气液两相流的交互模拟可以增强真实感,可广泛用于游戏、动画及影视制作等;在实际工程中,如针对水利工程中的问题,研究气液交互也有重要作用,只有很好地把握波浪与结构的相互作用关系,研究波的传播、高度差引起的水跌、水底气泡浮升时空气体积因压力所引起的变化、正在下降的水滴运动,或者是摇晃密度不同流体所引起的界面流动等,才能更好地增加工程的稳定性和可靠性。

目前,常用光滑粒子流体动力学 (smoothed particle hydrodynamics,SPH)方法进行液体模拟。 SPH积分时,邻近边界粒子的支持域会被问题域截断,这种单边影响会导致求解结果出现较大误差,因此必须通过一些特殊方式对边界进行处理,且处理应该尽可能小地对整个流场产生扰动。因此,在SPH方法中,边界处理一直是研究的重点和难点。在应用SPH方法模拟流体时,在气液边界处的流体粒子附近,流体粒子数目急剧减少,因此存在边界截断误差问题,从而影响流体模拟的精度以及模拟的稳定性。常见的处理气液边界的方法主要有2种,即虚粒子法和空气粒子法。

虚粒子法是在靠近气液边界的流体粒子上方生成若干层虚粒子,用来填补流体粒子被边界截断的支持域。文献[2]应用SPH方法模拟流体时,首次对气液边界粒子密度的计算方法进行了改进,虽然模拟效果提升得不明显,但是这为后续研究气液边界奠定了基础;文献[3]在气液边界粒子上方镜像生成多层虚粒子,参与表面张力的计算并作用于小型气泡,但是该方法产生的虚粒子的密度值差异较大,且数值变换剧烈;文献[4]提出泰特方程来降低不可压缩性,并且利用高阻尼方程初始化粒子,使靠近自由表面的粒子能够达到相对稳定的密度值,但是该方法只适用于初始粒子形状规整、分布均匀的情况;文献[5]提出ghost方法,利用Poisson-disk算法生成的虚粒子具有稳定的状态分布,但是该算法的计算量较大;文献[6]提出一种气体压力法来生成虚粒子,与ghost方法相比,该方法计算量减少、耗时短,但是气液表面的精度和细节有所降低;文献[7]先在流体模拟域内初始均匀分布ghost粒子,且ghost粒子位置保持不变,再利用一个判定机制选出自由表面处的ghost气体粒子,该方法一定程度上解决了动态生成ghost粒子困难的问题,但是在容器较大、流体运动比较平缓的情况下,预先固定镜像粒子将造成一定的浪费;文献[8]提出一种空气粒子均匀化分布的方法,将空气粒子和流体粒子看成同一种粒子进行处理,在所有的粒子之间另外施加一个余弦函数的力,在一定时间步空气粒子可以达到足够的均匀状态,但加入余弦函数意味着增加了很多的计算量,降低了模拟效率。

空气粒子法是把空气也看作一种流体,则气液边界也是一种液液边界,只是两相粒子的密度比为1∶1 000。因此,如何处理该密度比的多相流交互成为处理气液边界的关键。文献[9]使用密度重整化方法,对空气粒子使用大的人工表面张力和较高的波速,使速度场平滑,但是需要非常小的时间步长来维持模拟系统的稳定,这导致模拟时间较长;文献[10]提出一种改进的多相SPH方法,并将其应用于流体工程以估算多流体的密度,该方法能够处理跨相交界面的密度不连续性,允许不连续的黏度,但是确保跨相交界面上的速度和应力的连续性,该方法的缺点是增加了计算量,且添加表面张力后的效果不是很理想;文献[11]改进SPH方法中的密度计算公式,模拟了密度比为1∶1 000的空气和水交互场景,但是该方法对多相流之间的波速比有较大的限制;文献[12]使用(密度加权)平均压力来处理气液边界上的压力梯度,但是边角处容易出现粒子不稳定的情况;文献[13]提出一种排斥力来稳定两种流体之间的界面,将其应用于密度比为1∶1 000的多相流模拟中,但是,该方法需要低密度粒子的数目是高密度粒子数的5～7倍,否则模拟效果较差,局限性较大;文献[14]利用压力泊松方程建模,使气液边界附近流体粒子的密度保持在一定范围内,但是该方法使体积守恒的误差比较大,且需要增加补偿项来处理交界面的密度不连续问题;文献[15-16]提出一种不可压缩SPH和弱可压缩SPH的耦合方法,对速度项应用不可压缩法,可压缩法将压力项作为界面处另一相的边界条件,又在可压缩相中加入人工黏度项用于界面的数值稳定,该方法可用于模拟密度比为1∶1 000和有较大波速比的多相流,但是,该方法实施起来比较麻烦,模型中不确定参数较多,模拟难度较大;文献[17]基于密度校正提出了一种新型WCSPH流体模型,该方法可以有效处理密度比为1∶1 000的气液交互面密度连续性问题,能够模拟与实际相符的波速比(4∶1)效果,但是该方法在气体粒子与液体粒子的数目比比较大的情况下,空气粒子会穿透水面,影响模拟效果。

与虚粒子法相比,空气粒子法更符合现实情况(空气也是粒子组成的),且在模拟多相流时,相数越多,空气粒子法优势越大,即不用为每相流的气液边界动态生成虚粒子,减少了计算量,更容易使多相流的气液边界保持稳定。

本文在处理气液边界时提取出界面粒子(气液交界处“最薄”的2层粒子),与这些界面粒子产生交互的粒子标记为“外交粒子”,这些“外交粒子”可用来加快界面粒子的邻近粒子搜索,也可用来处理气液边界。通过实验模拟时间对比发现,相比于文献[18],本文方法可以有效减少模拟时间,提高模拟效率。本文提出一种改进的空气粒子法压力求解公式,将其应用于上述的“外交粒子”来达到处理气液边界的目的。通过实验模拟效果对比发现,相比于文献[17]方法,本文方法使得气液交界面更光滑、清晰和无穿透现象。

1 SPH方法

SPH方法[19]中,在支持域Ω上,关于位置矢量r的属性方程f定义为:

(1)

其中,r′为邻近粒子位置矢量;δ(r-r′)为狄拉克函数,即

(2)

在数值计算中用光滑函数W(r-r′,h)来取代狄拉克函数,则f(r)为:

(3)

其中,W为平滑核函数;h为核函数的有效支持长度。

采用粒子近似方法来对核函数插值离散,粒子i的场函数值可以通过核函数对该粒子支持域内所有粒子函数值加权平均得到,即

(4)

其中,N为流体粒子i邻近域内的粒子总数;j为粒子i的邻近粒子;mj为粒子j的质量;ρj为粒子j的密度。

对f(r)求梯度与求拉普拉斯运算即是对核函数进行梯度运算与拉普拉斯运算,即

(5)

(6)

2 界面粒子的邻近粒子搜索

在用SPH方法模拟气液多相流运动时,一个必要的步骤是提取界面粒子,主要用来计算曲率(用于表面张力计算)和表面追踪(用于表面重建);另一个必不可少的步骤是搜索每个粒子的邻近粒子,这也是模拟中最耗时的步骤。在气液多相流中,当气液交互较为剧烈时会产生大量的界面粒子,如图1所示。图1中,绿色和红色粒子分别是A和B中的界面粒子。本文为界面粒子增加一个新功能,即帮助气液多相流中所有相流的界面粒子搜索它们的邻近粒子。

A—气相流 B—液相流图1 气液多相流中的界面粒子示意图

在提取界面粒子时,将与界面粒子交互的粒子提取并存储,这些粒子称为“外交粒子”(与本身所在相流的界面粒子或者其他相流的界面粒子产生交互的粒子)。在计算界面粒子属性需要搜索其邻近粒子时,只需要在“外交粒子”集合中遍历即可。

界面粒子一定是“外交粒子”,“外交粒子”不一定是界面粒子,如图2所示。图2中,绿色和蓝色粒子都是“外交粒子”。

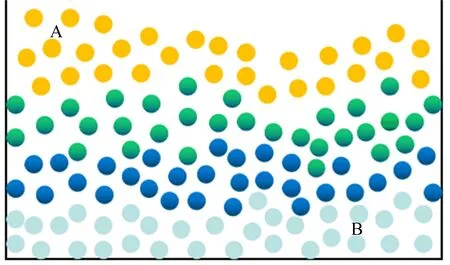
图2 气液多相流中的“外交粒子”示意图

本文气液多相流模拟的主要步骤如下:

(1) 初始化粒子位置,赋予粒子初始属性。

(2) 提取界面粒子[18],在提取界面粒子过程中即可提取出“外交粒子”集合。

(3) 遍历粒子,搜索每个粒子的邻近粒子,计算目标粒子的密度、压力、速度及加速度等属性。当目标粒子为界面粒子时,邻近粒子只需要在“外交粒子”集合中搜索。

(4) 更新粒子位置,返回到步骤(2)。

3 压力修正求解公式

利用文献[17]方法处理密度比为1∶1 000的气液交互面密度连续性问题时,在气体粒子与液体粒子的数目比比较大的情况下,空气粒子会穿透浪花,使得水波或浪花不正常断裂,呈现出类似一串珍珠的样子(应当只在浪的前端出现破碎、细小及飞溅的浪花),气液交界面的局部存在粒子穿透与“毛糙”界面。出现上述情况的原因是文献[17]模型中压力求解公式在细节处的不适用,即在求解气体粒子属性时,特别是在气液边界处,容易产生数值不稳定,产生较大速度和压力,穿透了聚集在一起的液体粒子团。

本文对“外交粒子”应用一个新压力求解公式(其他粒子仍使用文献[17]中的压力求解公式),以防止气液交界面发生粒子穿透和气液粒子混合影响交界面的清晰、光滑度。

“外交粒子”i的压力求解公式为:

(7)

(8)

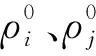
根据(7)式,粒子i受到粒子j的作用力为:

(9)

粒子j受到粒子i作用力为:

(10)

(7)式对支持域中有不同相粒子的“外交粒子”增加了压力修正项,使液体表面更光滑,具体分析如下。

(11)

则对这部分粒子不进行压力修正,(7)式化为:

(12)

(13)

(13)式可防止不同相粒子在界面出现穿透现象,并保持界面清晰和光滑,这与实际情况保持一致(与物理上的相斥流体界面现象相对应,即当流体与另外一种与其不相容的流体相互接触时,交界面上的力会保持界面的光滑性与清晰性)。

4 实验结果与分析

实验采用文献[17-18]和本文的方法模拟多相流溃坝场景。实验在Window 7系统上,平台为Visual Studio 2013。

4.1 界面粒子的邻近粒子搜索

采用文献[18]方法和本文通过提取“外交粒子”方法加快界面粒子中邻近粒子搜索的方法模拟多相流(4.2中气液交互场景),粒子总数为5 000、10 000、20 000、40 000时,2种方法的关键帧用时如图3所示。

图3 4种粒子总数下关键帧用时对比

4组实验模拟总时长对比见表1所列。模拟帧数均为2 342帧,实验效率提高程度η计算公式为:

(14)

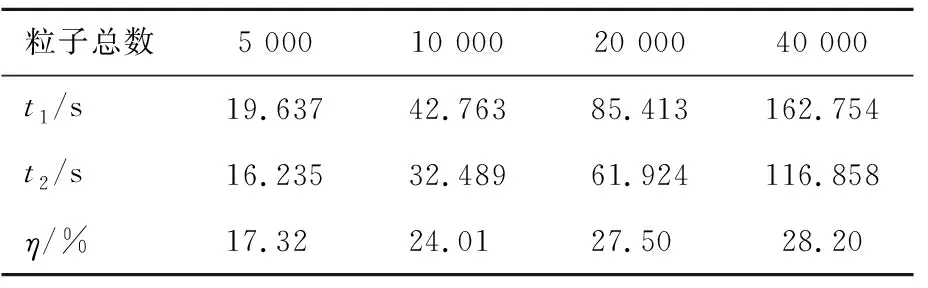
表1 4种粒子总数下模拟时长与实验效率对比

其中,t1为文献[18]方法用时;t2为本文方法用时。

从4组实验结果对比可以看出,本文方法能够提高模拟效率,增强模拟实时性。本文方法主要是加快对表面粒子中邻近粒子的搜索,当模拟场景中的粒子数较多且多相流之间交互剧烈(交互剧烈会产生大量的界面粒子)时,与文献[18]方法相比,本文方法不仅提升了模拟效率,而且稳定性更好,因此本文方法能更高效地处理复杂场景。

4.2 气液边界压力修正

应用文献[17]方法和本文方法模拟气液交互的场景。

气液交界面模拟效果对比如图4所示。图4中,黄色是空气粒子,红色是流体粒子。

从图4可以看出,在气液交界面,文献[17]方法存在粒子穿透与不光滑界面(用黑色圈标记),本文方法界面更光滑、更清晰,且没有穿透现象。

图4 气液交界面模拟效果对比

风吹水面二维模拟效果对比如图5所示。图5a、图5b中,从上至下是使用不同参数模拟不同“风力”的模拟效果。

图5 风吹水面二维模拟效果对比

从图5可以看出,采用文献[17]方法出现水波不正常断裂,呈现类似一串珍珠的样子,与实际不符,模拟效果不佳;采用本文方法模拟的水波连续且光滑,与现实相符,模拟效果有明显提升。

应用本文方法进行三维渲染实验的效果如图6所示。

图6 本文方法三维渲染实验效果

5 结 论

本文基于SPH方法提出一种多相流气液边界处理方法,解决了以下2个问题:① 针对气液边界交互粒子多,传统SPH方法搜索邻近粒子比较耗费时间的问题,本文通过提取“外交粒子”来减少搜索界面粒子邻近粒子的时间,该方法对于粒子总数多、交互剧烈的多相流模拟,效率有显著提高;② 针对气液交互面出现粒子穿透,交界面不光滑、“毛糙”等问题,本文对“外交粒子”应用一种新的压力计算公式达到处理气液边界的目的,使得交界面清晰、稳定且没有粒子穿透现象。多个仿真实验结果验证了本文方法的有效性。