一道调研题的多阶分析及拓展
2020-11-04 06:51江苏省海门中学226100顾旭东
中学数学研究(江西) 2020年10期
江苏省海门中学 (226100) 顾旭东


(1)求圆C的方程;

解读:本题是一条原创题,入手容易,前二问中规中矩有梯度,作为期中调研的压轴题,最后一问“求λ+μ的值”设置巧妙,在解析几何范畴内前后呼应,令人拍案叫绝,拨开云雾,让我们层层推进,多角度的来打磨这道调研试题.
对于原题,首先我们可以从特殊到一般进行分析.


图1


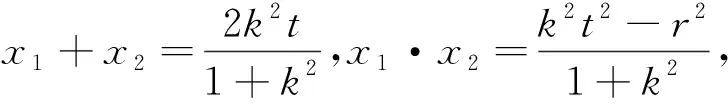
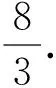


图2






图3



数学的简洁美在此体现的淋漓尽致,在我们顿足感叹时,不能忘了继续前行.

图4
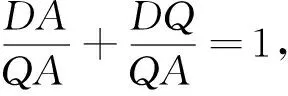


下面我们给出相关的拓展题目.
例1 已知抛物线y2=2px(p>0),过定点Q(t,0)的直线与抛物线分别交于A(x1,x2),B(x2,y2),如图4,过A作x轴的垂线(垂足为H),连BO并延长和Q点处与x轴垂直的直线交于G点,求证:四边形AQGH为平行四边形.

图5
例2 已知抛物线y2=2px(p>0),过定点Q(t,0)的直线与抛物线切于A点,如图5,过A作x轴的垂线(垂足为H),连AO并延长和Q点处与x轴垂直的直线交于G点,
求证:kAQ=kGH.
例3 已知抛物线y2=2px(p>0),A(x0,y0)为抛物线上任一点,过A作抛物线的切线l,l与x轴交于(x1,0),求证:x0+x1=0.
结语以上这些是对一条期中调研题的深入思考,在课堂教学中,我们更应该通过小步子、多角度、慢节奏地引领学生去思考,提高其学习的主动性和积极性,让其爱上数学,只有这样,数学的核心素养才能真正意义在学生的心灵深处,生根发芽.
猜你喜欢
新世纪智能(教师)(2021年2期)2021-11-05
小学生学习指导(中年级)(2021年10期)2021-11-01
红蜻蜓·低年级(2021年9期)2021-09-22
新世纪智能(数学备考)(2021年11期)2021-03-08
中学生数理化(高中版.高二数学)(2020年10期)2020-11-10
小学生作文(中高年级适用)(2018年5期)2018-06-11
福建中学数学(2016年8期)2016-12-03
初中生世界·七年级(2014年2期)2014-03-24

