一道质检函数压轴题的多解及推广
四川师范大学数学科学学院 (610068) 纪定春 夏逸天
函数压轴题是高考数学的重要题型.从直接法、导数定义法、指数不等式法、拉格朗日中值定理法、柯西中值定理法、洛必达法则、等价替换、函数凹凸法等视角,对一道百校联盟2020届教育教学质量监测函数压轴题进行了解法探究,并对该题进行了推广.
1.试题呈现、分析与评注

(1)讨论函数f(x)在(0,+∞)上的单调性;
(2)若对任意的x∈(0,+∞),f(x) 分析:问题(1)运用导数方法易得,过程略.对于问题(2),欲求f(x) 评注:该试题的形式优美、结构简单、思路开阔、解法多样,且蕴含丰富的数学思想,如分类、参数、极限、构造、化归等思想,是一道值得探究的好题,下面将主要对问题(2)进行解法探究和推广. 此处可继续用柯西中值定理、洛必达法则、构造导数定义,此处不再给出具体的步骤. 解法6:(洛必达法则)由解法2可知:a< 推广3 对任意x∈(0,+∞),不等式xex>1+ax+lnx恒成立,求实数a取值范围. 提示:用xex=elnx·ex=ex+lnx>1+x+lnx,当且仅当“x+lnx=0”时等号成立. 推广4 对任意x∈(0,+∞),若不等式xex>1+x+lnx+a(x+lnx)2恒成立,求实数a取值范围. 推广5 对任意x∈(0,+∞),n>0,若不等式xenx>1+ax+lnx恒成立,求实数a取值范围. 提示:解决方法同推广3.当且仅当“nx+lnx=0”时,等号成立. 推广6 若对任意x∈(0,+∞),n>0,若不等式xenx>1+nx+lnx+a(nx+lnx)2恒成立,求实数a取值范围. 推广7 对任意x∈(0,+∞),m>0,若不等式xmex≥1+x+mlnx+a(x+mlnx)2恒成立,求实数a取值范围. 提示:解决方法同推广4、6.当且仅当“x+mlnx=0”时,等号成立. 推广8 对任意x∈(0,+∞),mn>0,若不等式xmenx>1+nx+mlnx+a(nx+mlnx)2恒成立,求实数a取值范围. 以上推广,可以根据学生的具体情况,有选择的将其纳入数学课堂教学.2.解法探究
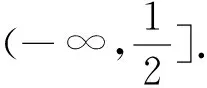
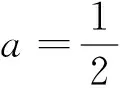


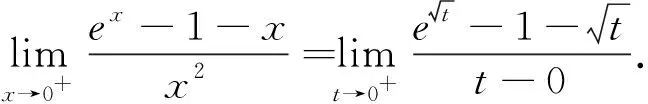



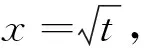
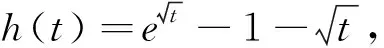

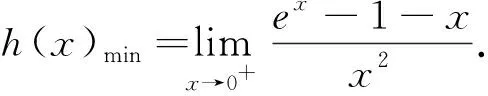
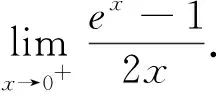
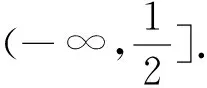

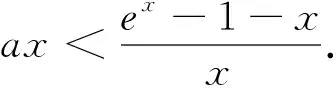
3.问题推广