函数应用核心考点综合演练
欧阳亮
一、选择题
1.函数y=x2-bx+1有一个零点,则b的值为( )。
A.2 B.-2
C.±2 D.3
2.函数f(x)=ln(2x)-1的零点所在的区间是( )。
A.(2,3) B.(3,4)
C.(0,1) D.(1,2)
3.已知定义在R 上的奇函数f(x)满足:当x>0时,f(x)=2x+2x-4。则f(x)的零点个数是( )。
A.2 B.3
C.4 D.5
4.函数f(x)=ex+x-3在区间(0,1)上的零点个数是( )。
A.0 B.1
C.2 D.3
5.设 函 数y=log2x-1 与y=22-x的 图像 的 交 点 为(x0,y0),则x0所 在 的 区 间是( )。
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
A.0 B.1
C.2 D.3
7.函数f(x)满足f(x+2)=f(x),且当-1≤x≤1 时,f(x)=|x|。若函数y=f(x)的图像与函数g(x)=logax(a>0,且a≠1)的图像有且仅有4个交点,则a 的取值集合为( )。A.(4,5) B.(4,6)C.{5} D.{6}
A.(0,1]
B.[1,+∞)
C.(0,1)
D.(-∞,1]
9.某位股民买入某支股票,在接下来的交易时间内,他的这支股票先经历了3 次涨停(每次上涨10%),又经历了3次跌停(每次下降10%),则该股民这支股票的盈亏情况(不考虑其他费用)为( )。
A.略有盈利
B.无法判断盈亏情况
C.没有盈利也没有亏损
D.略有亏损
二、填空题
13.某人计划购买一辆A 型轿车,售价为14.4 万元,购买后轿车每年的保险费、汽油费、年检费、停车费等约需2.4 万元,同时汽车年折旧率约为10%(即这辆车每年减少它的价值的10%),试问大约使用____年后,用在该车上的费用(含折旧费)达到14.4万元。
14.某公司为激励创新,计划逐年加大研发资金的投入。若该公司2016 年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是_____年。(参考数据:lg1.12=0.05,lg1.3=0.11,lg2=0.3)
(1)求函数y=g(x)的解析式。
(2)若方程f(x)=a 在x∈[0,1]上有且仅有一个实数根,求实数a 的取值范围。
17.已知函数f(x)=log2(2x+1)。
(1)求证:函数f(x)在(-∞,+∞)上单调递增。
(2)若g(x)=log2(2x-1)(x>0),且关于x 的方程g(x)=m+f(x)在[1,2]上有解,求m 的取值范围。
(1)求f(50)的值。
(2)试问如何安排甲、乙两个大棚的投入,才能使总收入f(x)最大。
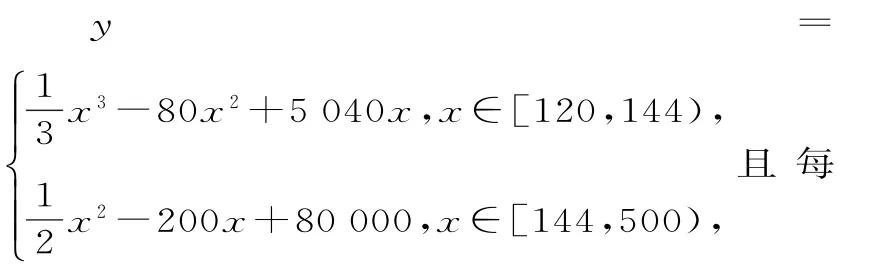
(1)当x∈[200,300]时,判断该项目能否获利。如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
一、选择题
1.提示:因为函数有一个零点,所以Δ=b2-4=0,所以b=±2。应选C。
2.提示:f(x)=ln(2x)-1 是(0,+∞)上的增函数,是连续函数,且f(1)=ln2-1<0,f(2)=ln4-1>0,根据函数零点的存在性定理可得函数f(x)的零点位于区间(1,2)内。应选D。
4.提示:由题意知函数f(x)是增函数。根据函数的零点存在性定理及f(0)=-2,f(1)=e-2>0,可知函数f(x)在区间(0,1)上有且只有1个零点。应选B。
7.提示:因为f(x+2)=f(x),所以f(x)的 周 期 为2。当x ∈[-1,1]时,f(x)=|x|。在同一直角坐标系中作出函数f(x)与g(x)=logax 的图像(图略)。若函数y=f(x)的图像与函数g(x)=logax(a>0,且a≠1)的图像有且仅有4个交点,则a>1且函数g(x)=logax 的图像过点(5,1),即a=5。应选C。
9.提示:设买入股票时的价格为m(m>0)元,先经历了3次涨停(每次上涨10%)又经历了3次跌停(每次下降10%)后的价格为
m×(1+10%)3×(1-10%)3=0.993m<m,
所以该股民这支股票的盈亏情况(不考虑其他费用)为略有亏损。应选D。
二、填空题
10.提示:因为函数f(x)是定义域为R的奇函数,且在(0,+∞)上是增函数,所以f(0)=0。又因为f(-2)=0,所以f(2)=-f(-2)=0。故该函数有3个零点,这3个零点之和等于0。
12.提示:将函数f(x)=log2(x+a)的零点x=1-a,代入x2-(a+1)x-4(a+5)=0得到(1-a)2-(a+1)(1-a)-4(a+5)=0,解得a=5或a=-2。
13.提示:设使用x 年后花费在该车上的费用达到14.4 万元。依题意可得14.4(1-0.9x)+2.4x=14.4,化简可得x-6×0.9x=0。令f(x)=x-6×0.9x,易得f(x)为单调递增函数。又f(3)=-1.374<0,f(4)=0.0634>0,所以函数f(x)在(3,4)上有一个零点。故大约使用4 年后,用在该车上的费用达到14.4万元。
三、解答题
因为240>200,所以当每月处理量为400t时,才能使每吨的平均处理成本最低。

