机场服务机器人模糊自适应PID控制系统仿真研究

周晨光，王 勇，唐火红，刘 洋，张祖芳，2

（1.合肥工业大学 机械工程学院，合肥 230000；2.合肥工业大学（马鞍山）高新技术研究院，马鞍山243000）

经济的飞速发展，人们对于航空出行的选择愈来愈多，机场本身具有空间及其人流量大，环境复杂的特点，其具有很高的服务压力，机场服务机器人能大大提高机场工作效率。 本文针对以麦克纳姆轮全向驱动为移动平台的机场服务机器人，设计一种稳定可靠的控制算法来控制麦克纳姆轮移动平台上的每个电机的运行状态。 从而实现整个平台的稳定移动。

传统的PID 控制系统虽然结构简单，但参数一经确定，不能在系统运行中进行更改，系统的调节能力仅取决于设定的Kp、Ki、Kd的初始值，在一些复杂多变的场景中，很难进行在线实时调节PID 的控制参数，因此在运行过程中往往会表现出较大的波动、甚至出现不可控的状态[1]。 针对上述情况，本文提出一种基于模糊控制的PID 控制器，并研究将其应用在机场服务机器人上。 根据制定的模糊规则，控制系统能够实现对PID 控制参数的动态调节，使该控制系统具有良好的动态性能和鲁棒性。

1 麦克纳姆轮移动平台控制结构

该移动平台控制系统框图如图1所示。 选用STM32 系列作为主控芯片。 芯片通过电机驱动板分别向四个直流电机发送四路PWM 脉冲。 编码器读取电机的转速并将其返回到主控制器中，形成闭环控制。 电机最终通过减速器将转速传递到对应的麦克纳姆轮上来实现预定运动。

图1 控制系统基本框图Fig.1 Basic block diagram of control system

2 直流脉宽调速系统数学模型的建立

麦克纳姆轮移动平台系统的控制对象是直流电动机，本设计所使用的电机型号为JGB37-520，编码器为AB 相输出的增量式光电编码器。

本文设计的电机调速系统采用直流脉宽调速系统实现对直流电机转速的调节。 调速系统采用闭环控制方式，反馈值为电机的瞬时转速[2-3]。 基于转速负反馈控制的直流脉宽调速系统的框图如图2所示。

本设计中，通过电机JGB37-520 和L298N 驱动模块的参数，通过查阅直流电动机选型手册的相关参数[4]，得出电压放大倍数Ks=3.64，Ts=0.00169 s，Tl=0.017 s，Tm=0.07 s，Ce=0.19。 考虑到PWM 信号发生器要求的输入范围为［-1，1］，故取K=0.1，反馈系数α=1。

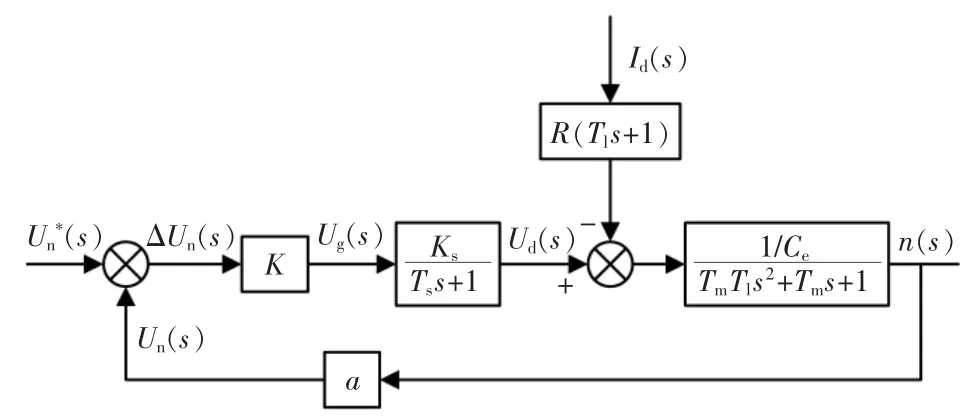
图2 基于转速负反馈控制的直流脉宽调速系统的框图Fig.2 Block diagram of DC pulse width speed regulation system based on speed negative feedback control

通过Matlab 内的Simulink 组件对调速系统数学模型进行搭建，如图3所示。

图3 电机调速系统框图Fig.3 Block diagram of motor speed control system

3 直流电机的控制策略研究

3.1 常规PID 控制器设计

本设计采用数字PID 控制中的增量式PID 控制算法，此算法相较于位置式PID 控制算法，只是针对控制量的增量进行处理，只与本次的偏差值有关，误动作时影响小。 增量式PID 控制算法流程如图4所示[5]。

采用临界比例法对PID 控制器的参数进行整定，初取比例系数Kp=14，积分系数Ki=838.3，微分系数Kd=0.992。 初取参数后，对其进行反复调整与比较，直到系统的动态过程达到相对最佳状态[6]。 得比例系数Kp=45，积分系数Ki=100，微分系数Kd=0.8。 加入PID 的控制系统调速框图如图5所示。

3.2 模糊PID 控制器设计

模糊PID 控制器结构框图如图6所示。 模糊PID 控制器选用Mamdani 型控制器，使该控制器持续获取误差e 和误差变化率ec 的数值，输入模糊控制器中将其模糊化，再依据模糊控制规则进行推理，将其清晰化，最终输出ΔKp、ΔKi、ΔKd到PID 控制器中，实现Kp、Ki、Kd的实时调整。 使直流电机具有良好的动态及静态性能[7-8]。

控制器的输入是计算出的误差e 和对应的误差变化率ec，输出是ΔKp、ΔKi、ΔKd，分别表示比例系数变化量、积分系数变化量、微分系数变化量。 将e，ec，ΔKp、ΔKi、ΔKd的模糊子集取为｛NB，NM，NS，ZO，PS，PM，PB｝，分别表示负大，负中，负小，零，正小，正中，正大。

考虑到三角形隶属度函数具有简单方便，同时在运行过程中不会占用系统过多内存的优点。 本设计中输入量e 和ec 以及输出量ΔKp、ΔKi、ΔKd的隶属度函数类型均选为三角形。其中输入量e 和ec 的论域都取为［-3，3］。 输出量ΔKp的论域为［-1，1］，ΔKi的论域为［-10，10］，ΔKd的论域为［-0.03，0.03］。 各变量对应的隶属度函数如图7所示。 其中变量子集的模糊交算法选为min，模糊或的算法选为max。

图5 加入PID 的控制系统调速框图Fig.5 Block diagram of speed regulation of control system with PID

图6 模糊PID 控制框图各变量及其隶属度函数的确定Fig.6 Determination of variables and membership function of fuzzy PID control block diagram

3.2.1 模糊控制规则的确定

根据参数Kp、Ki、Kd对系统输出特性的影响效果，一般遵循以下原则来建立ΔKp、ΔKi、ΔKd的模糊规则表：

（1）当∣e∣较大时，选用较大的Kp来提高系统的快速性，选用较小的Ki来防止较大的∣e∣导致的微分溢出，选用较小的Kd来减小系统的超调量；

（2）当∣e∣和∣ec∣的值为中等大小时，需适量减小Kp同时选用适中的Ki和Kd来防止产生过大的超调量；

（3）当∣e∣很小时，选用较大的Kp和Ki使系统具有良好的稳态性能，并选取适当的Kd来避免系统震荡，即当∣ec∣较小时，Kd应选取的大一些，当∣ec∣较大时，Kd应选取的小一些。

根据以上原则建立的ΔKp、ΔKi、ΔKd模糊规则表见表1、表2和表3。

表1 ΔKp 的模糊规则表Tab.1 Fuzzy rule of ΔKp

表2 ΔKi 的模糊规则表Tab.2 Fuzzy rule of ΔKi

表3 ΔKd 的模糊规则表Tab.3 Fuzzy rule of ΔKd

将以上规则写成if…then…的格式，一共得到以下49 条规则：

3.2.2 输出模糊量的清晰化

本设计采用重心法（centroid），由下式算出：

式中：ucen表示面积中心对应的横坐标；uj表示对应离散变量的横坐标；A（uj）表示uj处的隶属度。

3.2.3 算法流程

本文控制系统算法流程如图8所示。

将采集的误差和误差变化率输入到模糊控制器中，通过模糊化、模糊推理以及清晰化一系列处理，输出对应时刻的比例系数、积分系数和微分系数的变化量，PID 控制器将这三个参数同上一时刻的对应参数进行相加从而得到新的PID 控制器参数，从而实现对直流电机的优化控制。

4 系统仿真及结果分析

为了验证算法的准确性，借助Matlab 软件，根据上述设计流程，将各变量及其隶属度函数和模糊控制规则在新建的FIS 文件中进行设置。 ΔKp、ΔKi、ΔKd的输出曲面分别如图9、图10和图11所示。

图9 ΔKp 在论域上的输出曲面Fig.9 Output surface of ΔKp on the universe of discourse

通过Simulink 搭建了移动平台直流电机常规PID 和模糊PID 调速系统仿真模型，并将模糊PID控制器导入到Fuzzy Logic Controller 模块中。 控制系统模型如图12、图13所示。

图10 ΔKi 在论域上的输出曲面Fig.10 Output surface of ΔKi on the universe of discourse

图11 ΔKd 在论域上的输出曲面Fig.11 Output surface of ΔKd on the universe of discourse

图14、图15、图16为给定直流电机控制系统一个单位阶跃信号和指定参数值的阶跃信号，分别采用传统PID 控制和模糊PID 控制策略下的系统输出曲线。 通过比较可以看出，与传统PID 控制策略相比较，模糊PID 的控制方法调整时间更短，系统响应速度更快。其各项指标参数如表4、表5、表6所示。

图12 常规PID 控制系统模型Fig.12 Conventional PID control system model

图13 模糊PID 控制系统模型Fig.13 Fuzzy PID control system model

图14 单位阶跃信号仿真对比Fig.14 Unit step signal simulation comparison

表4 阶跃信号下各控制系统主要参数指标Tab.4 Main parameter index of each control system under step signal

图15 指定值20 的阶跃信号仿真对比Fig.15 Step signal simulation comparison with a specified value of 20

表5 指定值20 的阶跃信号下主要参数指标Tab.5 Main parameter indicators under a step signal with a specified value of 20

图16 指定值50 的阶跃信号仿真对比Fig.16 Step signal simulation comparison with a specified value of 50

表6 指定值50 的阶跃信号下主要参数指标Tab.6 Main parameter indicators under a step signal with a specified value of 50

图17为在2.5 s～3.5 s 期间给定直流电机控制系统一个随机干扰信号时，常规PID 在加入随机扰动时最大的超调量为25%，模糊PID 在加入随机扰动时最大的超调量为17%，并且相比于常规PID 有更快的响应时间。 即具有更好地扰动抑制能力。

图17 加随机干扰后仿真对比Fig.17 Simulation comparison after adding random interference

通过以上对比结果可以说明，相比于常规PID控制，模糊PID 在动态控制性能与抗扰动能力方面更具有优势，而且实时性好、鲁棒性强。 因而更加适用于对于驱动稳定有较高需求的机场应用环境。

5 结语

本文通过Matlab/Simulink 工具，对麦克纳姆轮移动平台的直流电机的调速系统进行建模分析，采用模糊逻辑的控制方法为常规PID 控制器实现参数的实时调节。 与常规PID 控制器在相同条件下得到的控制结果比较表明，模糊PID 控制器比常规PID 控制器具有更小的超调量，更快的响应时间和调整时间。 具有良好的动态性能和对外来扰动的抗干扰能力，对于机器人移动平台在机场环境下的驱动稳定性具有更好的效果。