基于不同空间插值法的黄海和东海北部 游泳动物多样性空间分布研究*
唐 政 单秀娟 关丽莎 金显仕2, 胡芷君 韩青鹏,4
(1. 上海海洋大学海洋科学学院 上海 201306;2. 青岛海洋科学与技术试点国家实验室海洋渔业科学与食物 产出过程功能实验室 青岛 266071;3. 中国水产科学研究院黄海水产研究所 农业农村部海洋渔业可持续发展 重点实验室 山东省渔业资源与生态环境重点实验室 青岛 266071;4. 中国海洋大学水产学院 青岛 266003)
为了探究变量在不同空间尺度上的分布格局和变化规律,通常要求采样信息具有空间上的连续性,但是受成本和技术等限制,对于高山、地层和海洋等难以到达或范围较大的研究区域,只能获取具有一定分辨率的分散样本点数据(Li et al, 2014),空间插值法可以利用有限的数据,对整个研究区域的变量进行 预测,减少采样调查的费用和难度,因此,被广泛应用于水文、气象、土壤、矿产、农业和生态等方面 (孙铭帅等, 2017; 岳文泽等, 2005)。空间插值法可以分为非地统计法、地统计法和二者结合的方法(Li et al, 2014)。受自身算法、数据本身属性以及样本点数量等多种因素的影响,不同情况下空间插值法的精度存在一定差异(朱会义等, 2004),例如,孙慧等(2017)研究发现,Cubist 方法预测的土壤Cd 含量结果精度较高;Chen 等(2016)发现,不同采样时间对渔业资源密度空间插值的精度存在差异;Luo 等(2011)对多种方法估算的月降水量的空间分布进行比较发现,协同克里格法(Ordinary cokriging, COK)的精度要高于泰森多边形法、反距离加权法(Inverse distance weighted, IDW)和普通克里格法(Ordinary kriging, OK)。因此,在实际应用时,有必要先对不同插值方法进行比较分析,选择最优的方法。
物种多样性在不同尺度上的空间分布特征是生态学研究中的重要问题(李圣法, 2005; 马斌等, 2008)。游泳动物作为水生生物群落的重要组成部分,其多样性空间变化可以在一定程度上反映物种多样性的变动趋势。目前,只在陆地生物多样性空间分布中发现不同空间插值法的比较研究(Hernandez- Stefanoni et al, 2006),虽然空间插值法在海洋生物多样性空间分布中已有应用(Stelzenmüller et al, 2009;Tittensor et al, 2010; 张敏等, 2011; 吕振波等, 2012),但是尚未见不同方法优劣的判别研究。因此,本研究比较分析了5 种常用的空间插值法[包括IDW、径向基函数法(Radial basis function, RBF)、局部多项式法(Local polynomial interpolation, LPI)、OK 和COK]对4 种多样性指数[即物种种类数(S)、Shannon-Weaver多样性指数(H’)、Pielou 均匀度指数(J)和Margalef丰富度指数(d)]的插值结果,选出最适合海洋游泳动物多样性插值的方法,以期为海洋生态学研究提供参考。
1 数据与方法
1.1 数据来源
数据来自2017年5月黄海和东海北部渔业资源底拖网调查,调查站位见图1。调查船为中国水产科学研究院黄海水产研究所“北斗”号,平均拖速为3.0 kn,拖网时间为0.5~1 h,调查网具网目尺寸为836目× 20 cm,囊网网目为2.4 cm,网具总长度为83.2 m。渔获物鉴定到种,并记录每一个种类的尾数和重量。数据分析前,将原始数据标准化为1 h的渔获尾数和渔获重量。
1.2 物种多样性指数
采用物种种类数(S)、Shannon-Weaver 多样性指数(H′)、Pielou 均匀度指数(J)和Margalef 丰富度指数(d)对游泳动物多样性进行分析,公式如下:
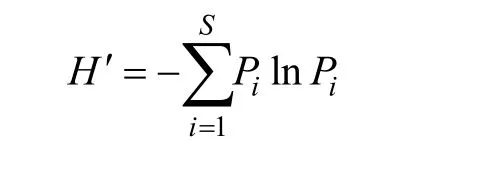

图1 黄海和东海北部调查站位图 Fig.1 Survey stations in the Yellow Sea and north East China Sea
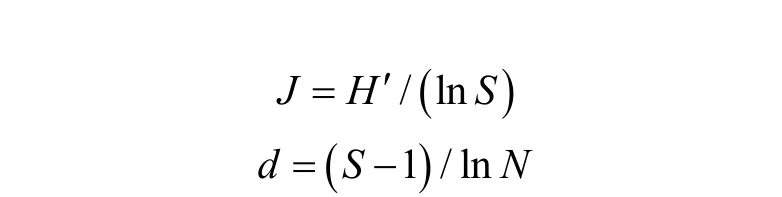
式中,S 为每个站位游泳动物种类数,Pi为第i种游泳动物重量占总重量的比例,N 为所有游泳动物的总重。
1.3 空间插值法
1.3.1 反距离加权插值 IDW 基于相近相似原理(Chaplot et al, 2006),假设每一个样本点的值都会对邻近区域产生影响,距离未知点越近的样本点对其影响程度越大。公式如下(Shepard, 1968):


以统计学上的无偏性和最优性为条件,结合拉格朗日原理,可推导出权重值和半方差函数之间关系的公式(王政权, 1999)。
1.3.5 协同克里格插值 COK 是利用主变量之间的相关性及其与辅助变量的交互相关性,优化插值的精度(姜勇等, 2006),常用于主变量数据难以获取或直接用主变量插值的结果不准确的情况(李润林等, 2013)。公式如下(Myers, 1982):

1.4 数据的正态分布检验和转换
进行OK 和COK 之前,数据必须符合正态分布,因此,对上文计算的4 种物种多样性指数数据进行Shapiro-Wilk 检验(Chen et al, 2016)。若不满足正态分布,则进行数据转换。因为数据结构存在差异,本研究采用BOX-COX 和平方2 种转换方式(于洋等, 2015; 章清等, 2016)。
1.5 效果评价
采用jackknife 检验比较不同空间插值法的预测效果。该检验的主要步骤为:首先,对于已有的n 个样本,依次去除其中1 个样本点,利用剩余的n‒1 个样本作为训练集对去除点进行估算,重复n 次,得到所有样本点的预测值;其次,计算预测值与样本实际观测值的决定系数(Coefficient of determination, R2)、平均绝对误差(Mean absolute error, MAE)和均方根误差(Root mean square error, RMSE)。R2反映样本值和预测值之间的相关程度,R2越接近1,表示该空间插值法的预测值与样本值的变化趋势越相似,反之则偏差越大;MAE 可以反映预测值可能的误差范围;MAE和RMSE 都可以反映插值结果的精度,且都是越小越好(林忠辉等, 2002; 董志南等, 2015; 于洋等, 2015)。公式如下:
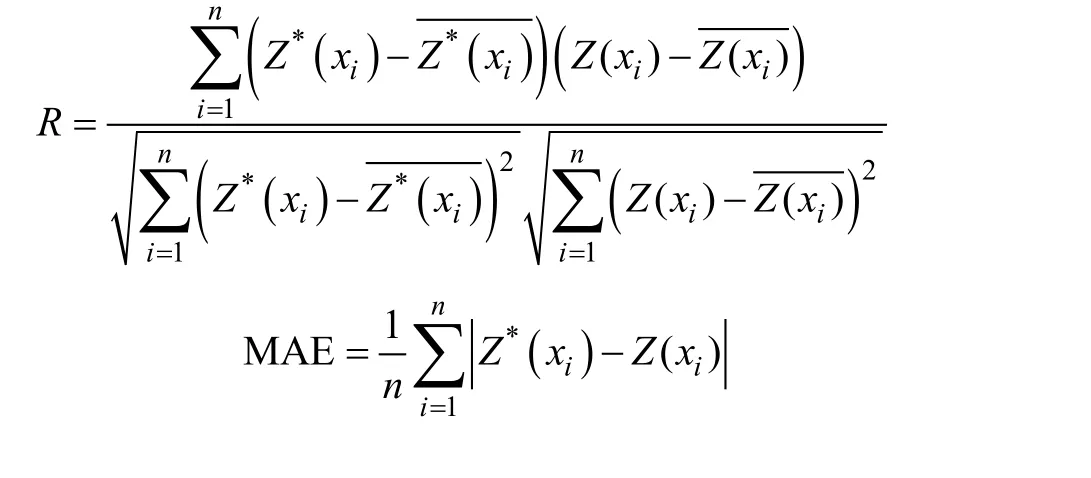

物种多样性指数计算及其描述性统计、MAE及R2的计算、数据的正态分布检验和转换采用R3.5.2完成;半方差函数的拟合采用GS+7.0软件完成,因GS+7.0软件无法计算具有多个辅助变量条件下的半方差函数,因此,COK的半变异函数中的C0、C和C0/C 3个参数是未知的,其变程的计算是由ArcGIS10.2完成;4种多样性指数之间的相关性判断采用SPSS17.0完成;坐标转换、空间插值和交叉验证采用ArcGIS10.2完成。
2 结果
2.1 数据的统计描述
4 种多样性指数的描述性统计见表1,Shpiro-Wilk正态检验发现,S、J 和d 属于偏态分布(P<0.05)。根据数据特点,对S 和d 进行BOX-COX 转换,对 J 进行平方转换,转换前对数据进行加1 处理。转 换后,数据均通过Shpiro-Wilk 正态检验(P>0.1),符合正态分布。此外,H′符合正态分布(P>0.05),不做转换。

表1 物种多样性指数描述性统计和Shapiro-Wilk 检验的P 值 Tab.1 Descriptive statistics of five species diversity indices and P-values of the Shapiro-Wilk test
2.2 协同克里格法辅助变量的选择

表2 列举了物种多样性指数之间的相关性,其中,S、H′和d 之间具有极显著的正相关关系。J 与H′呈极显著正相关关系,与d 呈显著正相关,而与S 相关性不显著。将具有极显著相关的物种多样性指数作为辅助变量,当存在多个具有显著相关的辅助变量
时,根据ArcGIS10.2 交叉验证的结果初步进行筛选。S 和J 最适合的辅助变量均为H′和d;H′最适合的辅助变量为S 和J;d 最适合的辅助变量为S、H′和J。
2.3 克里格插值半方差函数分析
根据GS+7.0 软件的拟合结果(表3),不同物种多样性指数的半方差函数适合不同的模型。S 的空间分布为中等空间相关性(C0/C=0.43),其他3 个指数均为强空间相关性(C0/C<0.25),符合空间插值的前提。不同物种多样性指数对应的变程差别较大:S 和d 的变程较大,说明其在大范围内的空间自相关性较强,H′和J 的变程都较小,说明在小尺度范围内二者的空间自相关性较强。
2.4 不同空间插值法的比较
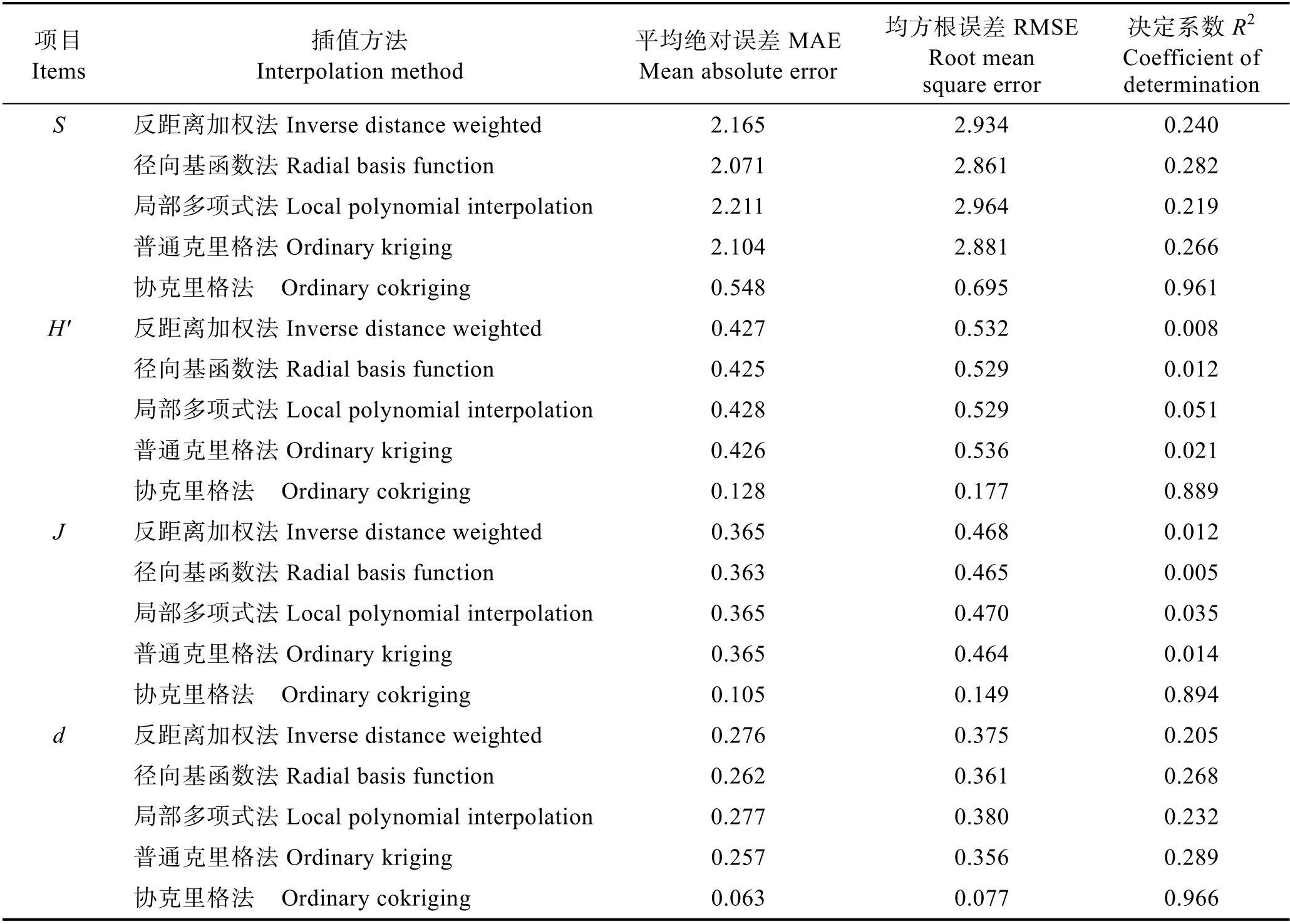
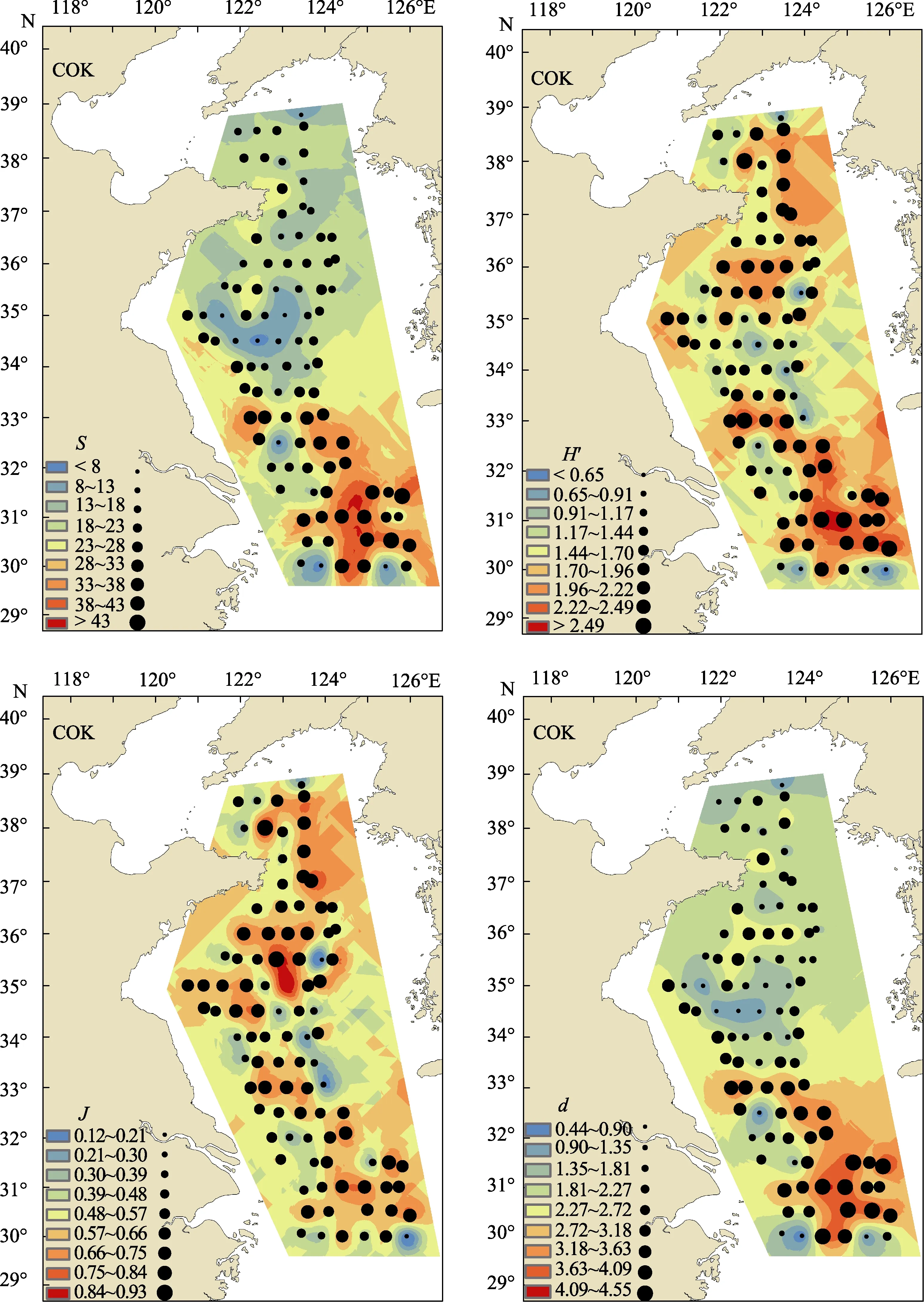
对于S,5 种空间插值法按预测值与样本值的R2大小排序为LPI 表3 物种多样性指数的半方差函数及相关参数 Tab.3 Semivariance models and the corresponding parameters of species diversity indices 4 种多样性指数在样本点的大小分布与预测的空间分布基本一致,在非采样区域的曲线平滑度都低于采样区域(图2)。S 和d 整体的空间分布格局相似,都呈现出明显的东南部高,北部次之,中部最低的格局。H′和J 也是中部最低,但是在南部和北部海域差异不明显。4 种多样性指数在32°N 以南海域高值区的范围大致相同。 分析COK的预测图,在大尺度上,2017年春季黄海和东海北部游泳动物的S和d大致呈现明显的南高北低的格局,而H′和J的南北差异不大。与台湾海峡游泳动物多样性(宋普庆等, 2012)以及相邻海域鱼类群落多样性(程济生, 2000)相比,除了d具有相同的空间格局,后2种多样性指数空间分布格局均有较大差别。在小尺度上,34°~35.5°N,121°~124°E附近海域的S和d明显比周围海域低,而H′和J在此范围内没有明显的低值区。在30°~32°N范围内的海域中,4种多样性指数均有高值区,而且西部海域均低于东部海域。在刘勇等(2017)的研究中,30°~32°N海域底层渔业生物的S和d也存在高值区,而且S、H′和d三者也呈现东部海域高于西部海域的格局,但是J在124°~ 126°E之间海域存在大范围的低值区,与本研究结果有较大差别。 游泳动物多样性指数空间分布变化特征可能与环境、优势种、饵料丰度及分布、栖息地状况、人为活动和鱼类洄游行为等多种因素有关(Jin et al, 1996; 戴芳群等, 2020; 金显仕等, 2009; 程济生等, 2004; 朱鑫华等, 1994)。从水文环境方面看,因为多样性指数与环境因子的相关关系可以量化,而且数据容易获取,常受到人们关注。已有研究表明,春季黄海中南部的S和d与海底水温显著正相关(P<0.05),与深度、海表温度和盐度关系不显著(P>0.05)(单秀娟等, 2014),说明物种多样性的空间分布可能受海底水温影响程度较大;而H’和J与深度、海底和海表的水温和盐度的关系不密切(单秀娟等, 2014)。受海底地形、海流等因素影响,在春、夏和秋季,黄海中北部海域存在一个稳定且大范围的冷水团(李洪波等, 2006; 于非等, 2006; 王家栋等, 2011)。而在2017年春季,35°N,122°~124°E附近海域的海底温度最高为10℃,低于附近海域的温度(孔凡洲等, 2018)。这可能是导致4种多样性指数在大尺度上以及34°~35.5°N,122°~124°E附近海域呈现独特的分布特点和差异的原因。对于30°~32°N范围内的东海北部海域,多样性指数较低的原因可能是靠近长江口受淡水冲击导致附近海域环境条件不稳定,海水浊度较高,不利于生物生活(Whitfield, 1994; 刘淑德等, 2009, 徐勇等, 2014)。从繁殖特性方面看,春季是很多游泳动物繁殖的季节,繁殖群体会洄游到环境适宜的海域产卵。如位于32°~34°N、122.5°E以西海域的吕四渔场是银鲳(Pampus argenteus)、小黄鱼(Larimichthys ployactis)和黄鲫(Setipinna tenuifilis)等种类主要产卵场(陈新军, 2004; 刘勇等, 2017)。在30°~32.5°N,123°~126°E之间的海域存在多个重要渔场,例如,舟山渔场、江外渔场和舟外渔场等,是多种重要渔业种类的产卵场(刘勇等, 2007、2014; 林龙山等, 2008)。影响游泳动物空间分布的原因复杂多变,对于其他小尺度上的多样性指数空间特征形成原因,还需要进一步研究和分析。 表4 不同插值方法的交叉验证结果 Tab.4 Cross-validation diagnostic of different interpolation methods 插值结果的精度取决于空间插值模型对变量空间变异性和相关性的解释度(朱会义等, 2004)。本研究中,4 种多样性指数的COK jackknife 检验结果都比较好,解释度高于其他方法,这与很多研究结果一致(卢月明等, 2017; 李润林等, 2013; 石朋等, 2005; 岳文泽等, 2005)。但是,在日降水量(宋丽琼等, 2008)和热带雨林植物多样性(Hernandez-Stefanoni et al, 2006)的空间插值法比较研究中,COK 的精度要低于OK。根据王平等(2014)对不同辅助变量的COK 插值结果比较,发现当主变量和辅助变量之间的相关性大于0.45 时,COK 精度才会明显高于OK。可见,辅助变量的选择是COK 插值的关键步骤,合适的辅助变量可以优化COK。目前,最简单的方法是直接将与主变量相关性较高的因子作为辅助变量。如果主变量有多个显著相关的因子,可以根据ArcGIS 软件交叉验证的结果进行初步筛选。但是,当与主变量显著相关的因子数量过多时,这种筛选方式会导致工作量增加,而且单一的辅助变量可能对模型优化程度有限(章清等, 2016)。因此,基于主成分分析的COK 受到广泛关注。这种方法是利用主成分分析,将多个与主变量显著相关的因子赋予不同的权重,再合并成综合指标作为辅助变量(卢月明等, 2017),在鱼类资源丰度和土壤要素的空间分布研究中都取得了较好的结果(方学燕等, 2017; 章清等, 2016)。 图2 协同克里格插值(COK)预测出的物种种类数(S)、Shannon-Weaver 多样性指数(H′)、 Pielou 均匀度指数(J)和Margalef 丰富度指数(d)的空间分布图 Fig.2 Spatial distribution of number of species (S)、Shannon-Weaver diversity index (H′)、 Pielou′s evenness index (J) and Margalef′s richness index (d) by ordinary cokriging (COK) 本研究采用了多个辅助变量,主变量与辅助变量之间的相关性很高,因此,相对于OK,COK 的精度有了极大提高。研究表明,S、H′、J 和d 之间存在较高的相关性,这种现象在不同季节和年份同样存在(单秀娟等, 2014),因此,COK 不仅可以用于分析和预测春季黄海和东海北部游泳动物多样性空间分布,还可能适用于不同时间维度。在今后的研究中,可以结合与游泳动物多样性有显著关系的环境因子,并基于主成分分析法减少辅助变量的数量,尝试进一步提高COK 的精度。
3 讨论与分析
3.1 黄海和东海北部海域游泳动物多样性空间分布
3.2 空间插值法分析
3.3 展望

