论电荷的相对论效应
罗锦添
(天津市双菱中学 天津 300040)
0 引言
1905年,爱因斯坦一连发表了5篇论文,其中有一篇论文中爱因斯坦提出了狭义相对论,这篇论文就是《论动体的电动力学》。在这篇论文中,爱因斯坦推导出了时间膨胀公式,尺缩效应公式,推翻了绝对时空的概念。在更早的时候,物理学家欧姆提出了欧姆定律和电阻定律,焦耳提出了焦耳定律。本文所做的工作就是将电阻定律、欧姆定律、时间膨胀公式、焦耳定律联立,推导出一个带电粒子的速度与电荷的关系方程。
1 时间膨胀公式
假设有一个人A相对于地面做匀速直线运动,相对于地面速度为v,加速度a=0。此时A手里拿着一个光钟,并且还有一个相对于地面静止的B正在观测A。在A看来,光钟里的光垂直于光钟内部的平面镜运动,且在A看来光反射一次(从光钟内部一块平面镜出发抵达另一块后发生反射,再抵达第一块平面镜,这一过程称为反射一次)的时间为2t。根据同时的相对性,B观测到光反射一次的时间不等于A观测到的,设B观测到光钟内部的光反射一次用时2t’。由于光钟相对A静止,以A为参考系,光钟内部的光在A运动方向上的位移矢量 =0。而由于A相对B匀速直线运动,所以光钟相对B运动。在B看来光钟内部的光的位移可以分解到垂直方向和平行于A运动的方向,以B为参考系,光钟内部的光的运动轨迹并不是一条直线,而是折线,即光与平面镜的夹角 ≠90°。根据光速不变原理,不论以A还是B为参考系,光钟内部的光速均为c。根据,以A为参考系时,从光钟内部一块平面镜C到另一块D,光的位移为:

以B为参考系,同一束光,从C到D,光的位移为:

以A为参考系时光束垂直于平面镜,故以A为参考系时光从C到D的位移矢量、以B为参考系时光的位移矢量及以A、B为参考系时同一束光抵达另一块平面镜的两个位置点构成的线段组成一个Rt△。根据勾股定理,

解方程,

2 尺缩效应公式
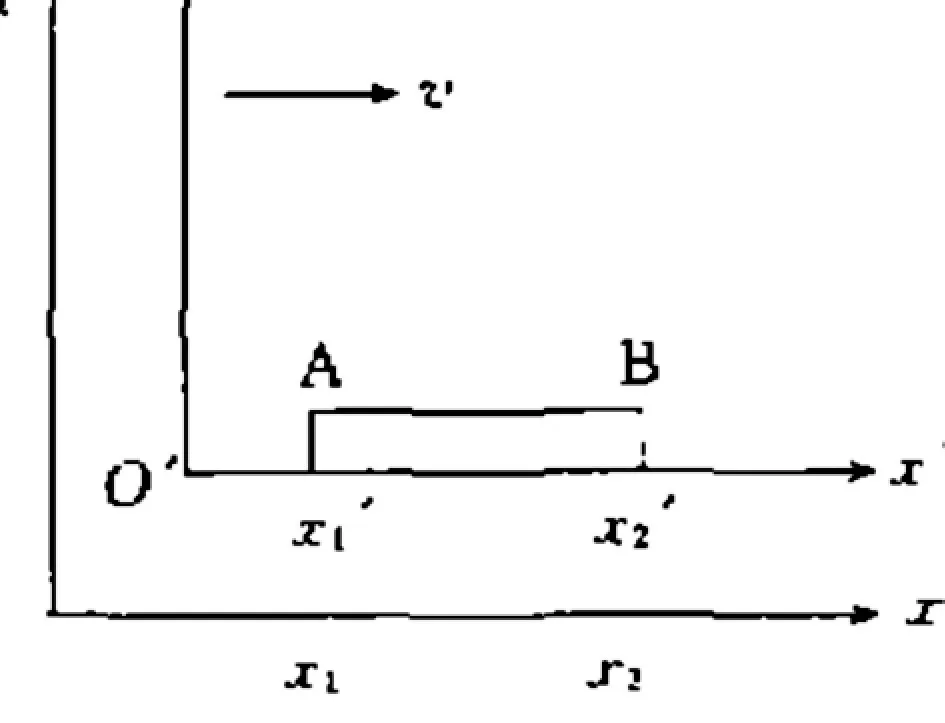
图1
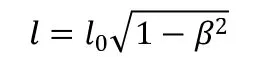
其中,=v/c。(4)即为长度收缩公式。
(图1中右上方的坐标系为k’,较大的坐标系是k。)
3 电荷的相对论效应
狭义相对论认为,所有物质都有两种质量:静止质量和运动质量,而且同一个物质相对于一个参考系运动速度越大,此参考系的观测者测得此物质的运动质量越大。物质的速度和运动质量的定量方程为:

其中m0为物质的静止质量,=v/c。对于同一种物质(没有物质多少的增减),质量是此物体的属性,同时质量(在相对论体系中为能动张量)为引力场的场源。那么,作为电场的场源,电荷有没有与(5)相似的变化方程呢?
假设有一个导体,导体中恒定通过电流为I的电子束,通电时间为t,显然此时导体带电。现此导体以接近光速的速度匀速直线运动,速度为v。则导体的电荷可表示为:

将(3)代入(6),

那么,考虑相对论效应后,通过导体的电流是否恒定呢?根据焦耳定律,

根据电阻定律,

将(4)代入(9),

由(8)得:

将(10)、(3)代入(11),
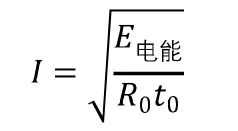
显然,通过导体的电流恒定。

将(12)代入(7),

对比(5)和(13)可知,电荷与质量相似,也有相对论效应。
4 虚拟绝对参考系
在狭义相对论的质速关系方程中,我们称0为静止质量。根据狭义相对论,静止是相对的,也就是说,静止质量不是恒定的,可以随着参考系的变化而变化。因为,物质携带的“固有能量”也不固定,能量不守恒,这绝对不可能。那么,相对论中的“静止质量”是指相对于哪一参考系静止呢?
牛顿在《自然哲学的数学原理》一书中提出了绝对时空的概念,他指出空间为绝对静止的参考系。目前已经证明了,即使是宇宙空间也在膨胀,空间并非绝对参考系,但是我们可以在数学上构造出一个虚拟的绝对参考系,0就是物质相对于这个虚拟绝对静止参考系静止时的质量,这个参考系在宏观、微观世界中都无法找到,但这个参考系确实真实存在。所以,物体的静止质量0无法测量,只能通过公式计算,公式为:
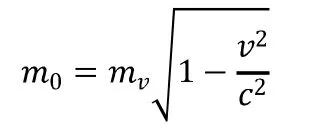
利用这个虚拟的绝对静止参考系,也可以解释惯性力。牛顿为了证明绝对空间理论,做了一个“水桶实验”,实验中水桶刚开始旋转时水因为受到惯性力而静止,所以牛顿说:物质是否受到惯性力不取决于物质的相互作用,而是此物质是否相对于绝对空间做非惯性运动。后来马赫指出,物质是否受到惯性力取决于它是否相对于宇宙加速,显然此理论是错的:宇宙本身就在加速膨胀,以宇宙空间为参考系,一个坐在桌前静止的人也会受到惯性力,这是不可能的。由于运动的相对性,如果一个物体是否受到惯性力是借助一个实体物质参考系判断的,那么可以得到如下结论:以此物体P为参考系,一个质点做加速运动,质点受到惯性力;如果以质点为参考系,P做加速运动,再次将参考系还原到P,由于参考系的变换,质点被赋予了一个虚拟的加速度a,此加速度与以质点为参考系时P的加速度相等,方向相反。所以,用来判断物质是否受到惯性力的参考系不是实体参考系,而是上文中我们引入的一个虚拟绝对静止参考系,当物体相对于虚拟绝对静止参考系做变速运动时物体就会受到惯性力。描述惯性力的公式为:。

