惯性力
文钦若 丁学成
(河北大学 河北 保定 071002)
1 与坐标系选取无关的力
在非相对论中关于力的基本概念有几个不成文的但值得注意的要点.
(1)力可以分为两类:第一类是与坐标系选取无关的力,即不论坐标系是否是惯性坐标系,其测量结果都是相同的;第二类是与坐标系选取有关的力.通常认为只有惯性力属于第二类力,而其余力都属于第一类力.在物理学开始部分讲述力的基本概念时通常不涉及第二类力.
(2)第一类力与坐标系无关的性质只能视为物理学中的公理,并没有作普遍性的证明,但可以作下述理解:当考虑一个质点所受的力为第一类力时,各施力的质点都是明确的,所以可认为第一类力只是相对位置、相对速度以及各质点固有性质的函数,而相对位置、相对速度以及各质点的固有性质都与坐标系无关.
(3)对于由牛顿万有引力定律得到的引力,显然应归属于第一类力.当不考虑牛顿万有引力定律时,或者在对施力物体不明确的情况下(例如,在对舱外一无所知的爱因斯坦舱内考虑舱内物体所受舱外物体的引力),也可以直接测量一个质点所受的引力,爱因斯坦的等效原理[1]指出,这种引力与惯性力是等效的而不可区分,则惯性力必影响对引力的测量.通常只能测量到这种引力与惯性力的合力,这时,应将这种合力归属于第二类力.若希望将引力与惯性力区分开来,则只能根据牛顿万有引力定律测量引力.
2 惯性参照物与惯性坐标系[2]
2.1 不考虑惯性力的情况
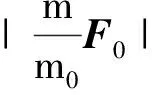
2.2 考虑惯性力的情况
惯性力与坐标系的选取有关,惯性力为零的坐标系便是惯性坐标系.通常测量一个质点所受惯性力的方法是:使惯性力与第一类力处于平衡状态,再通过测量第一类力而得到惯性力.设参照物所受第一类力为F0(其中包括引力),但在相对此参照物静止或做匀速直线平动的坐标系中,此参照物应不受力,所以测量到此参照物所受的惯性力必为-F0.显然,在这种坐标系中,当第一类力F0为零时,第二类力即惯性力-F0也为零.这时,相对于参照物静止或做匀速直线平动的坐标系就是惯性坐标系,相应的参照物就是惯性参照物.从以上的分析可知,考虑与不考虑惯性力,所得到的惯性坐标系与惯性参照物是相同的.
2.3 引力与惯性力不可区分的情况
设某坐标系K相对于惯性坐标系做匀加速直线平动,则此坐标系K中质点m的运动方程可表示为
F1+Fg+Fi=ma
(1)
其中Fi为惯性力,Fg为引力,F1为其他第一类力.如果Fg不是根据牛顿万有引力定律得到的引力,而是直接测量到的质点m所受的引力,则Fg与Fi是不可区分的,这时,由于观察者不能判断出在合力(Fg+Fi)中是否含有惯性力,所以也不能判断出坐标系K是否是惯性坐标系.如果在质点m的运动范围内引力场是均匀的,且Fg+Fi=0,则质点m的运动方程化为
F1=ma
(2)
另一方面,设坐标系K相对于某参照物或者静止或者做匀速直线平动,如果此参照物所受的引力为F0,所受的其他第一类力为零,则由于在坐标系K中此参照物所受的惯性力应为-F0,所以此参照物所受引力与惯性力的合力应为零.当引力与惯性力不可区分时,也不能判断出坐标系K是否是惯性坐标系.
3 惯性力的测量
作为例子,设火车在水平面上在恒力Ft的作用下做匀加速直线运动,考虑在火车上相对火车静止(或做匀速直线平动)的坐标系中怎样测量惯性力?
3.1 Ft不是引力或主要不是引力的情况

3.2 Ft完全是引力的情况
在质点的自由落体中,使质点加速的力是重力.对于火车,Ft是引力或主要是引力的情况是很难实现的,但为了将有关概念说清楚,可假设这种情况是存在的.当Ft为万有引力时,此引力也必作用在小球与火车中的人体上.设火车范围内的引力场是均匀的,则由于引力与质量成正比,在人体上不会因引力作用而产生形变,从而使得火车中的人在不视听窗外时不可能感觉出火车是否做加速运动.无论火车是否做加速运动,弹簧都不伸长,这是由于作用在小球上的引力与惯性力的合力为零之故.这时,在火车内部可以根据式(2)讨论弹簧振子的运动.为了测量出火车所受的惯性力,应先测量出引力Ft,Ft可在其他惯性坐标系中测出,若在火车中则只能根据牛顿万有引力定律得到.测出Ft后,便可推知火车所受的惯性力为-Ft,而小球所受的惯性力为
3.3 Ft为引力与摩擦阻力之差的情况
当引力的值大于摩擦阻力的值而使火车做加速运动时,火车中的人也可根据身体形变而感觉出火车是否做加速运动,但当火车向前加速时,面向车头的人不是向后仰而是向前倾.当火车向前加速时,对于桌面上的弹簧,设r指向车头,则弹簧将伸长,这时,弹簧作用在小球上的力等于小球所受的引力与惯性力的合力,只有再测量出小球所受的引力才能得到小球所受的惯性力.
参考文献
1 俞允强.广义相对论引论.北京:北京大学出版社,2002
2 漆安慎,杜婵英.力学.北京:高等教育出版社,1997

