一种基于AKAZE算法的山区无人机影像匹配*

邓仕雄，闫星光，刘继庚，邹 宇，何清平

(1.贵州水利水电职业技术学院，贵州 贵阳 551416; 2.中国矿业大学(北京) 地球科学与测绘工程学院，北京 100083)

近年来无人机发展迅速，计算机科学结合测绘行业的应用更加广泛，无人机影像匹配对影像拼接、数据分析、三维建模等关键技术具有重要意义。前人对相关领域做了大量研究，1999年David G.Lowe提出了尺度不变特征变换(Scale Invariant Feature Transform,SIFT)特征匹配算法，并于2004年对SIFT算法进行了改进和完善[1-2]。该算法基于尺度空间进行变换，最初应用于识别领域，近年来被推广到图像拼接领域，得到了长足发展。后来Bay等人提出了SURF(Speeded Up Robust Features)特征匹配算法[3]，SURF算法立足于SIFT算法，通过引入快速积分和滤波盒子，该算法对图像的平移、旋转或缩放等多尺度具有良好的效果，是一种稳健性很高的特征提取算法。为了满足实时性的需求，Ethan Rublee等人在2011年提出了ORB算法[4]，ORB算法结合了FAST[5]及Brief[6]算法并赋予FAST方向，该算法特征点具有旋转不变性，相比SIFT、SURF算法耗时更低。针对SIFT及SURF算法在构造尺度空间时，高斯模糊不保留对象边界信息且所有在尺度上平滑到相同程度的细节及噪声，这影响了定位的准确性，2012年在ECCV上提出了一种比SIFT算法更稳定的特征检测算法KAZE[7]并在此基础上做了改进，该算法采取非线性扩散滤波，相比SIFT、SURF提高了可重复性及独特性，算法计算较为密集，它通过引入快速显示扩散数据框架(FED)来快速求解偏微分方程以及引入一个高效改进局部差分的二进制描述符(M-LDB)，算法具有更好的重复性及鲁棒性[8-9]。

张冬梅等[10]针对无人机影像重影、失真及耗时等问题，通过改进算法对影像进行网格划分，求解每个网格的单应性矩阵，提出了一种改进的APAP算法，较大地提高了匹配效率及匹配效果。文献[11-14]在顾及有效约束条件、匹配鲁棒性、图像变化、匹配耗时等方面通过改进算法得到了较好的匹配效果。在前人研究的基础上，结合山区无人机影像峰林、峰丛较多，影像存在相互之间的遮挡及阴影等特征的影响，影像探测特征点较少，局部区域匹配难度大、匹配率低，造成难以获取较为完善的地理信息，本文通过改进算法能够有效的克服影像由于地形起伏大及地块特征破碎带来的影响，更好的剔除特征点误匹配，提高了匹配率。

1 影像匹配原理

1.1 SIFT算法匹配原理

SIFT尺度不变特征变换算法是把影像中探测的关键点用一个128维的特征向量进行描述，因此一幅图像经过SIFT算法表示为一个128维的特征向量集，该特征向量集具有对图像缩放、平移、旋转不变等特征。SIFT算法特征匹配主要涉及极值点检测、特征点精确定位、确定特征点方向、生成特征向量。尺度空间的构建其目的在于找到在尺度变化中具有不变性的位置，一个二维影像的尺度空间及高斯函数定义如下：

(1)

式中，G(x,y,σ)为高斯函数;I(x,y)为原始图像;*表示卷积运算。高斯金字塔是经过一系列的尺度空间变换和下采样得到。通过高斯差分可以在尺度空间中找到稳定不变的极值点，高斯差分函数D(x,y,σ)定义为：

D(x,y,σ)=[G(x,y,kσ)-G(x,y,σ)]*I(x,y)

(2)

式中，kσ和σ为连续影像的平滑尺度，所得到的差分图像在高斯差分金字塔中。通过对高斯差分空间拟合处理，获得极值点的位置及尺度，同时为了提高关键点的稳定性，舍去边缘位置的极值点。为了使描述符具有旋转不变性，需要利用图像的局部特征给每一个关键点分配一个基准方向。使用图像梯度的方法求取局部结构的稳定方向，在完成关键点的梯度计算后，使用直方图统计邻域内像素的梯度和方向。如图1所示，为图像梯度及加权后主方向。

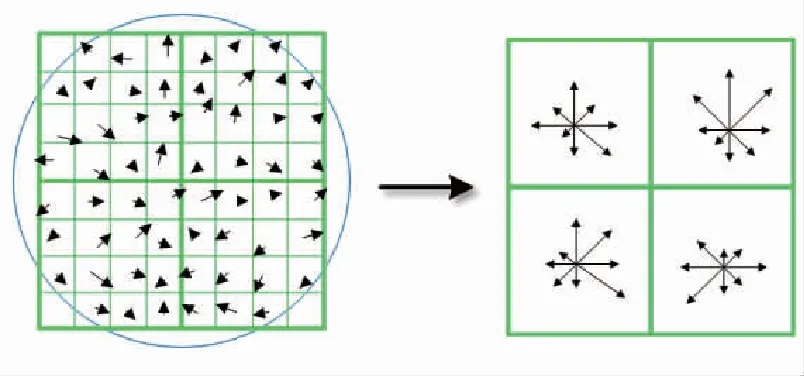
图1 图像梯度及加权后主方向

图中箭头方向代表每个像素的梯度方向，箭头长度代表梯度模值，最后需对其进行加权运算。通过统计的4×4×8=128个梯度信息为该关键点的特征向量，即每个特征形成4×4×8=128维的描述子，特征向量形成后，为了去除光照变化的影响，需要对它们进行归一化处理。

1.2 SURF算法匹配原理

SURF (Speeded-Up Robust Features)算子是SIFT算子的加速版，该算子在保留SIFT算子优良性能基础上，同时解决了 SIFT 算子复杂度高、耗时长的缺点，SURF算法对兴趣点提取及其特征向量描述方面进行了改进，且计算速度得到提高。算法使用海森矩阵(Hessian)的行列式值作特征点响应侦测并用积分图加速运算，基于 2D 离散小波变换响应Harr小波并且有效地利用了积分图。积分图像的加减运算计算公式如下：

(3)

式中，ρ(r,c)为图像中点(r,c)的灰度值。ii(i,j)可以通过迭代两次计算得到。通过使用不同的模板尺寸即可形成多尺度响应的金字塔图像，在响应的图像上，点x处尺度为σ的H(x,σ)定义如下：

(4)

Lxx=G(x,y,σ)⊗I(x,y)

(5)

式中，Lxx为标准高斯函数G(x,y,σ)的二阶偏导与图像在点(x,y)处卷积后的结果。一般使用9×9的模板对图像进行滤波的结果作为最初的尺度空间层，积分图像离散化导致两个层之间的最小尺度变化量，大小为盒子滤波器模板尺寸的1/3。滤波器尺寸计算公式如下：

FilterSize=3(2octave×interval+1)

(6)

SURF算法通过一个以特征点为中心以及张角为60°的动窗口来求取主方向值，具体以弧度0.2左右并旋转该窗口，并累加窗口内的图像Harr小波响应值dx、dy，得到一个矢量统计响应值在∑dx、∑|dx|、∑dy、∑|dy|形成的特征矢量。图2以特征点为中心并以20 s为边长，主方向用特征点到矩形边框的线段表示。统计各子块的响应值，最终得到各子块的矢量。

图2 特征描述子表示

1.3 AKAZE算法匹配原理

SIFT、SURF等特征检测算法是通过构建金字塔以及多尺度来消除噪声和提取显著特征点，该类特征匹配方法牺牲了局部精度，导致影像边界模糊和细节丢失。AKAZE算法通过改进局部差分二进制描述符以及引入快速显示扩散数据框架求解偏微分方程。非线性扩散滤波描述图像亮度的演化是通过提升尺度参数作为热扩散函数的散度因子来控制扩散过程。通常采用偏微分方程进行求解，由于涉及微分方程非线性性质，通过图像亮度的扩散来构建尺度空间。经典非线性扩散方程如下：

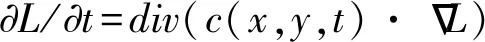
(7)

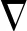
1.4 基于多约束条件的RANSAC精匹配

具有一定重叠度的无人机影像特征点数量并非相同，本文采用FLANN快速搜索结合KNN算法[15]，基于多约束条件的RANSAC算法[16]剔除误匹配点对，实现无人机影像精匹配。随机抽样一致性(RANSAC)算法是通过采用不断迭代的方法寻找最优参数模型，筛选出“外点”，使得满足大小为的最佳单应性矩阵H数据点个数最多，由于矩阵H有8个未知数，则至少需要4组匹配点对。本文结合RANSAC算法实现精匹配步骤如下：

(1)随机从AKAZE算法探测的特征点中抽4个样本数据(样本之间不能共线)，计算出变换矩阵H，记为模型W。

(2)将所有数据与模型W的投影误差进行计算，满足模型W的点个数与投影误差小于阈值φ则加入内点集Q。

(8)

式中，(x,y)为影像角点位置；(x′,y′)为场景影像角点位置；s为尺度参数；h11、h12、h33为矩阵元素。

(3)当内点集Q元素个数大于最优内点集Q-best，更新Q-best=Q，同时更新迭代次数k。如迭代次数大于k,则退出，否则迭代次数加1。重复上述步骤，可得到具有一定重叠度的影像匹配变换模型，剔除不满足模型的错误点对，通过该方法提高影像的匹配准确度，影像匹配正确率如式(9)。

(9)

2 试验及分析

本文利用SIFT、SURF、基于改进后的AKAZE算法三种算法分别对分辨率为像素的影像对进行匹配实验。试验运行环境为Intel(R) Core(TM) i5-2430M CPU @ 2.40 GHZ，运行内存6GB的笔记本电脑，基于VS2013的OpenCV2.4.10图像处理数据库作为数据处理平台。本次试验数据为贵州省安顺市龙宫景区无人机影像，如图3影像对(a)。由图可知，影像对地形起伏较大，地物特征丰富，局部区域特征点探测难度大。

图3 影像对(a)

2.1 试验过程

基于三种算法分别探测影像对(a)特征点，并采用FLANN快速搜索结合KNN算法筛选特征点，基于单映射变化矩阵的RANSAC算法进行精匹配。由于篇幅有限，本文只列出部分特征探测及匹配效果，如图4为改进后算法探测影像对的特征点显示图，图5～图7为3种算法影像对的匹配效果图。

图4 改进算法影像对特征点探测

图5 SIFT算法匹配效果图

图6 SURF算法匹配效果图

2.2 结果分析

试验数据地形起伏大，地块较为破碎，试验分析可知影像局部区域特征点较少甚至特征点难以探测，本文分别利用SIFT、SURF、改进后三种算法对影像进行试验，从特征点匹配对、耗时及精度进行对比分析。由表1可知，三种算法匹配率分别为94.5%、89.8%、100%，改进后算法匹配率更高，SURF算法存在误匹配且该算法耗时相对较低，SIFT及改进算法由于高斯金字塔及非线性尺度空间的构建耗时量相对较高。试验结果表明：改进后的算法在山区无人机影像特征点探测及匹配率性能更优，较好地克服了影像由于地形起伏及地块特征破碎带来的影响，有效地剔除了错误特征匹配点对。

图7 改进算法匹配效果图

表1 试验数据统计表

3 结 语

本文针对山区无人机影像匹配，通过改进算法，并从匹配对数、耗时及匹配率三方面对无人机影像进行试验对比分析。从试验结果来看，针对地形起伏大的山区无人机影像，基于改进后的AKAZE算法匹配率更高，相比另外两种算法，本文算法是一种稳定有效的无人机影像匹配方法，具有更优的鲁棒性及匹配性能。