多元变量总体最小二乘法在坐标转换中的初探*

钟阳弟

(广东省国土资源测绘院,广东 广州 510000)

三维激光扫描仪获取建筑物或者构件的点云数据时，往往需要多测站扫描。如果在扫描时可以直接得到相邻两站同名点的地理坐标，可以将测站坐标转换至统一的地理坐标系下进行拼接；若采用靶球等作为公共点传递或者其他无法得到相邻测站公共点地理坐标的，一般采用序列拼接的方式，依次进行坐标转换，坐标转换的误差将会传递与积累，使得最终模型拼接精度不高。因此，高精度求得坐标转换参数尤为重要。本文引用多元变量总体最小二乘非迭代方法对系数阵和观测向量进行改正，能较好地解决系数矩阵和观测向量存在随机误差的问题，同时又能易于编程实现，快速计算。

1 最小二乘法

陈义等提出了一种基于空间大旋转角的坐标转换方法[1]，该方法简单严密，适用性广。旋转矩阵9个参数中有3个独立变量，其余6个为非独立旋转参数，因此将三维基准转换模型进行泰勒级数展开，将9个方向余弦作为未知变量，建立包含13个未知参数的观测方程，再利用旋转矩阵的正交性作为限制条件，列出平差模型[2]。当控制点数量大于3时，通常采用最小二乘的方法建立误差模型进行解算。对于观测方程y=Aξ，就是假设观测矩阵A不包含随机误差，只有观测向量y包含随机误差。本文对最小二乘法函数模型不做详细推导阐述。

2 多元变量总体最小二乘法

最小二乘法采用的误差模型认为所有误差都包含在目标系统[3]中，即观测方程无需改正。事实上每一种测量值都包含各种各样的误差(如粗差、人为误差、模型误差和取样误差)，所以设计矩阵A也是包含未知的随机误差的，此时再用传统的误差模型求出的参数估值并不是最优的，这是由于模型误差引起的。而采用总体最小二乘方法建立误差模型，就可以同时考虑观测矩阵和系数矩阵包含的随机误差问题[4]，从而得到更精确的参数解。

Felus等[5]提出的同方差相似变化表达为：

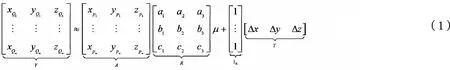
总体最小二乘方法的误差函数模型及随机模型如下：

Y-EY=(A-EA)R

(2)

RTR=I

(3)

(4)

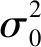
vec(EY)T·vec(EY)+vec(EA)T·vec(EA)=min

(5)

即误差平方和最小：

(6)

所以构造Lagrange目标方程：

(7)

式中,λ为n×3 Lagrange乘向量。由(7)式对各未知数求导得：

(8)

联立五式得到：

(9)

(10)

将式(9)、式 (10)带入式(6)得：

(11)

再将式(3)分别带入到式(9) 、式(11)得：

(12)

(13)

所以若旋转矩阵R已知，则上式是只关于变量的方程式，要使等式左边最小，将等式右边展开得：

(14)

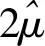
(15)

(16)

该方法验后单位权中误差的计算公式采用

(17)

(18)

旋转角度可以根据下式计算

(19)

式中,Rij为旋转矩阵R中第i行j列元素；εx,εy，εz分别为笛卡尔坐标系中绕坐标轴XY和Z的旋转角。

所以计算误差模型中最优相似转换参数的步骤总结如下：

(2)进行SVD分解：ATY=U∑V；

(3)令D=diag(1,1,det(UVT))；

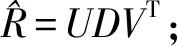
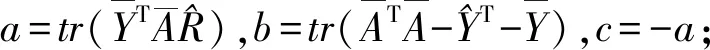
式中，1n是n×1阶各元素都为1的列向量。

3 实验分析

为了论证上述算法的正确性、可行性及精确性，本次实验采用最小二乘迭代算法(LS)和多元变量总体最小二乘法(简称PSTLS)两种算法，编写程序利用实际数据进行计算，分别从参数估值、单位权中误差、坐标较差等几个方面对结果进行对比和分析。已知某新体育馆框架结构中一个构件的刚体坐标系和测量坐标系下的两套坐标，坐标如表1所示。刚体结构坐标是相对位置坐标，采用的坐标系方向：X为北、Z为东、Y向上，原点为构件端点铰的中心，且为右手系。测量采用的坐标系方向：X为北、Y向东、Z向上，原点为任意假设，且测量坐标系为左手系。两个坐标系的指向存在未知的夹角，均采用重心坐标系进行数据计算，用各程序算出坐标转换参数结果如表2所示。

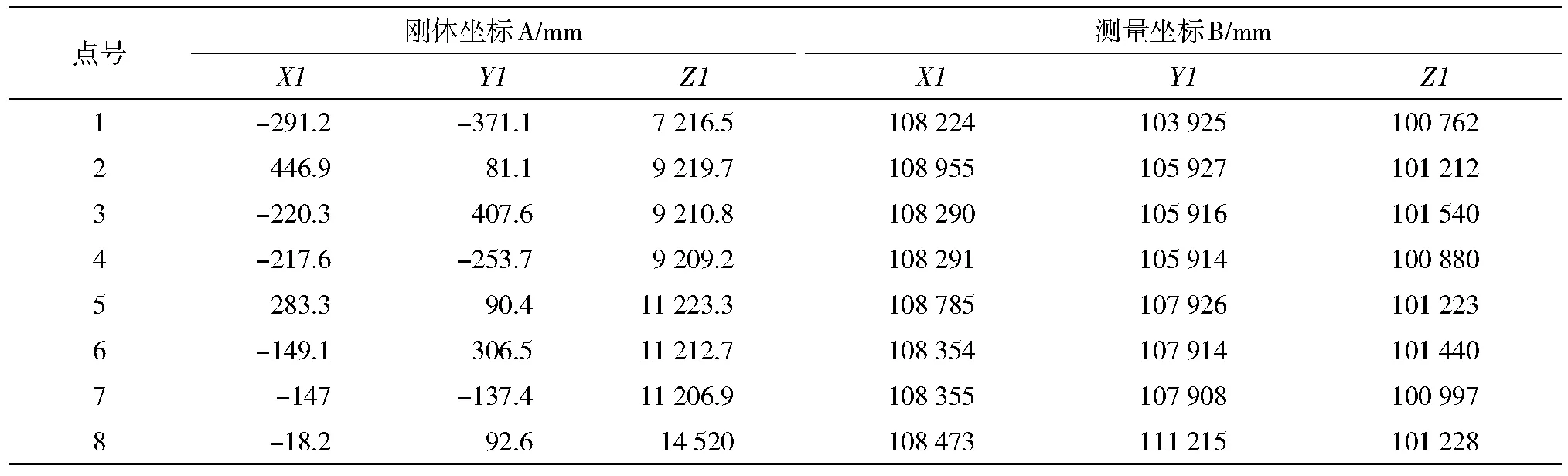
表1 刚体坐标系和测量坐标系下对应点坐标

表2 LS和PS-TLS计算出的坐标转换参数

分别利用LS和PS-TLS两种方法计算的关键节点坐标值和已知坐标值的对比差值如表3所示。

由LS和PS-TLS两种方法计算结果的精度如表4所示。

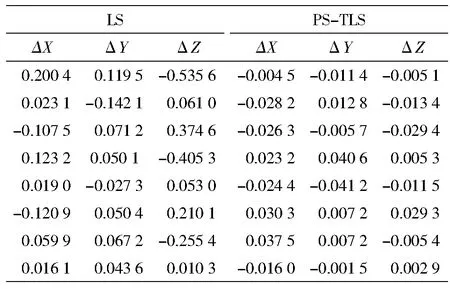
表3 LS和PS-TLS法计算出的已知点坐标差/mm

表4 三种方法坐标转换精度比较

由转换精度可知PS-TLS法比LS法精度更高，从转换的已知点坐标差值看，PS-TLS法的差值更小。两种方法从精度方面都达到了0.1 mm级，能满足常规工程应用，方法可行。运算过程中，LS法耗时112 s，PS-TLS法耗时23 s，效率上讲PS-TLS法更优。

4 结 语

最小二乘迭代法主要是将非线性模型转换为线性模型[8]，可用于任意角度的旋转，包括左、右手系坐标之间的转换，而无需预先知道旋转角度的近似值。但是需要设定初始参数值，且对参数初始化要求较高，要求参数初值必须在收敛半径内，否则无法收敛。而多元变量总体最小二乘法是一种严格意义上基于点对点的配准方法[9]，精度高，可以转换任意角度的两套坐标系，计算过程中没有矩阵求逆，在球形标靶分布不均匀或者数量较小的情况下，也能得到高精度的解算，该算法还易于编程实现。该方法在点云拼接过程中能够极大程度上提高拼接精度，简单可行。

但它只是同方差的3D转换，如果两套坐标点集的坐标精度不一致，还需要考虑对观测数据加权，然后再带入算法计算。后续对加权总体最小二乘法[10]的研究以及在点云拼接过程的精度影响还需进一步研究。