旁侧基坑开挖偏心卸载下盾构隧道横断面受力变形研究

刘亚宇， 刘加湾， 魏 纲, 3, *， 黄 睿

(1. 绍兴文理学院土木工程学院， 浙江 绍兴 312000； 2. 杭州融大齐云置业有限公司， 浙江 杭州 310026；3. 浙大城市学院土木工程系， 浙江 杭州 310015)

0 引言

近年来，随着城市地铁隧道规模越来越大，在既有地铁隧道附近不可避免地要进行各种开挖。基坑开挖会在邻近盾构隧道周围产生附加应力，破坏隧道原有的受力平衡，从而引发隧道的不均匀变形。在北京、广州、上海、深圳等城市均发生过由于基坑开挖施工引起的邻近地铁隧道安全事故[1-2]，对地铁运营造成严重威胁。因此，研究基坑开挖对邻近运营隧道的影响具有十分重要的意义。

结合国内外文献，目前关于基坑开挖卸载对盾构隧道结构影响的研究主要分为现场实测[3-4]、理论计算[5-9]、模型试验[10-11]、有限元模拟[12-15]等。况龙川[3]和蒋洪胜等[4]通过实测分析，得出基坑开挖中围护结构变形会影响邻近隧道，且隧道位移与基坑的距离有关。魏纲等[8-9]推导出基坑侧壁卸载产生的附加荷载计算公式，并通过改变基坑尺寸、β值以及隧道轴线深度，研究不同影响因素下隧道的受力情况；基于文献[8]的基坑开挖模型，进一步研究了旁侧基坑开挖对邻近既有盾构隧道的影响，并推导出管片错台量和环间转角的计算公式。陈俊生等[12]和石钰锋等[13]采用三维有限元模拟基坑开挖对邻近隧道的影响，得出采用分块对称开挖能很好地控制隧道变形。结合目前的研究可知，在基坑施工对邻近地铁隧道影响分析方面，现有研究大多针对隧道纵向变形，且只针对对称卸载工况，对横截面变形和受力以及偏心卸载工况研究较少，且大部分数值模拟只针对单环衬砌。针对这些不足，需要作进一步的研究。

本文采用MIDAS/GTS NX软件建立三环的精细化盾构管片模型。基于修正惯用法计算的盾构衬砌环初始围压和Mindlin公式计算得到的基坑开挖卸载产生的附加围压，通过将总的围压施加在盾构管片模型上，模拟计算得到盾构衬砌的横向变形和内力；采用椭圆度作为评价隧道安全状况的指标，研究基坑开挖偏心卸载对盾构隧道的影响规律。

1 盾构隧道围压计算

1.1 基坑开挖力学模型

图1为基坑与旁侧隧道位置关系图，在盾构隧道旁侧有1个矩形基坑，该基坑侧壁分别编号为①、②、③和④。隧道外径为D，以该基坑中心为o点建立空间坐标系，x轴与y轴分别垂直和平行于隧道轴线，z轴以竖直向下为正方向。以平行于基坑隧道方向的尺寸为l、垂直于隧道方向的尺寸为B，基坑开挖深度为h0+H1，基坑围护结构总深度为H=h0+H1+H2，围护结构至隧道的净距为s，隧道轴线埋深为h，基坑侧壁①紧邻隧道。

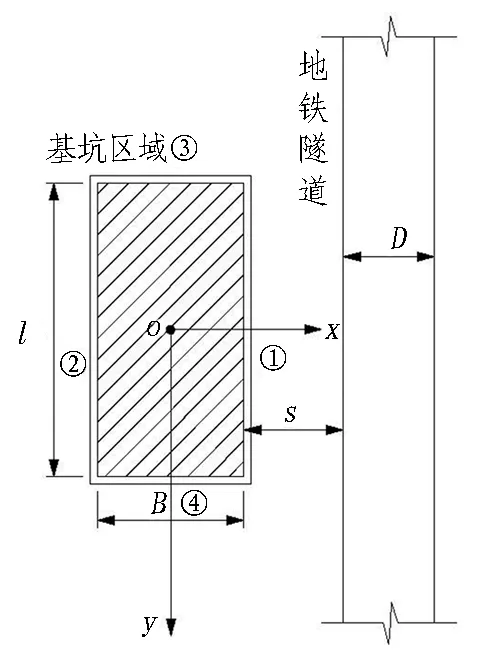
(a) 平面图

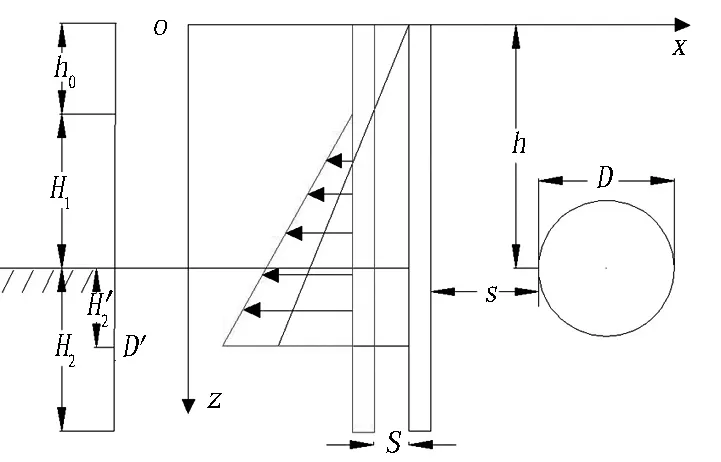
(b) 剖面图

图1 基坑与旁侧隧道位置关系图

Fig. 1 Position relationship between foundation pit and tunnel

1.2 围压计算方法

1.2.1 初始围压

当隧道旁侧基坑还未开始施工时，隧道承受初始的地层水土压力等荷载作用。根据文献[16-17]，采用修正惯用法，得到隧道初始工况下的荷载组合，见图2。初始工况荷载组合包括： 1)衬砌自重g； 2)上覆土竖向土压力q； 3)侧向主动土压力pe； 4)静水压力pw； 5)拱底反力qR； 6)各项荷载作用下管片环发生变形后侧向的土体抗力pk。由于三维计算模型采用地层弹簧模拟地层抗力，因此，在计算初始荷载时不应考虑三角形假定的地层抗力。

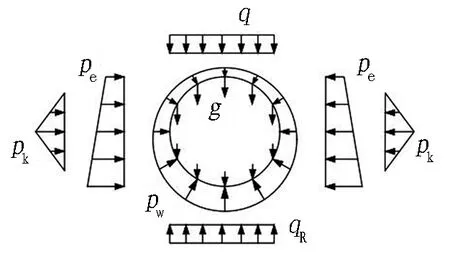
图2 初始荷载组合示意图

1.2.2 附加围压

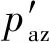
图3 附加荷载组合示意图

1.3 案例验证

邻近上海地铁1号线某基坑[18]可简化为盾构隧道与基坑东北侧围护结构平行。基坑平面开挖尺寸l=70 m、B=42 m。地下水位以上h0=2.3 m，墙前后水位差H1=7.7 m，h0+H1=10 m。围护结构至隧道的净距s=7.2 m，基坑以下深度H2=12 m，基坑底部以下

文献[9]通过Matlab编程实现数值运算得出隧道的水平位移分布规律。图4为不同围护结构位移工况下隧道水平位移对比，隧道水平位移以指向基坑侧为负值。通过计算可知，当S/Sacr=2/5时，基坑侧壁应力系数β=13.9%。此方法计算得到的隧道水平位移值和该工程实测数据相吻合。可见，参考文献[5]将β值取25%来计算本工程是不合理的。以下有限元模拟将根据S/Sacr=2/5(β=13.9%)来进行。

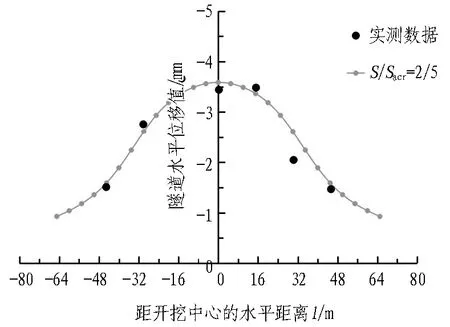
图4 不同围护结构位移工况下隧道水平位移对比

图5为不同围护结构位移工况下β值的变化。可以看出，随着S/Sacr逐渐增大，β值和隧道最大水平位移值也逐渐增大，但随着围护结构位移达到极限值时，两者的增长速率会逐渐减慢。可知，基坑围护结构位移刚开始会产生较大的附加荷载，对隧道的影响较为显著，之后随着卸荷率增长速率减慢而导致隧道所受到的附加荷载减少，最大水平位移增长速率也逐渐减少。

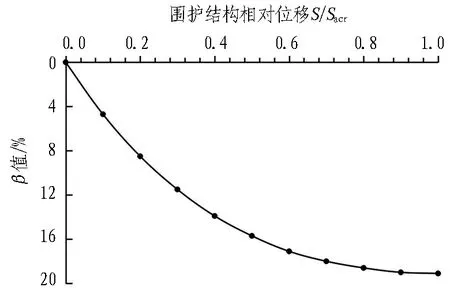
图5 不同围护结构位移工况下β值的变化

通过文献[16]计算出初始围压，再根据文献[17]算出实际工程中的附加围压，叠加算出最终围压变化值。围压计算结果如表1所示，表1中角度对应的位置指的是垂直方向围绕隧道横截面中心顺时针旋转一定角度后的位置，如90°指的是横截面上最右端的位置。

2 三维有限元模型建立

2.1 模型基本假定

假定： 1)在管片中，仅对管片之间连接的螺栓进行模拟，忽略其他钢筋的影响，将混凝土理想化为各向同性的材料； 2)除了管片间螺栓，忽略橡胶密封垫等其他部件的影响； 3)忽略螺栓孔与螺栓之间的空隙，并假设管片与管片、管片与螺栓在开始时均为紧密连接； 4)忽略混凝土材料的耐久性性能对混凝土材料本身强度的影响； 5)只分析盾构隧道衬砌横向的力学行为。

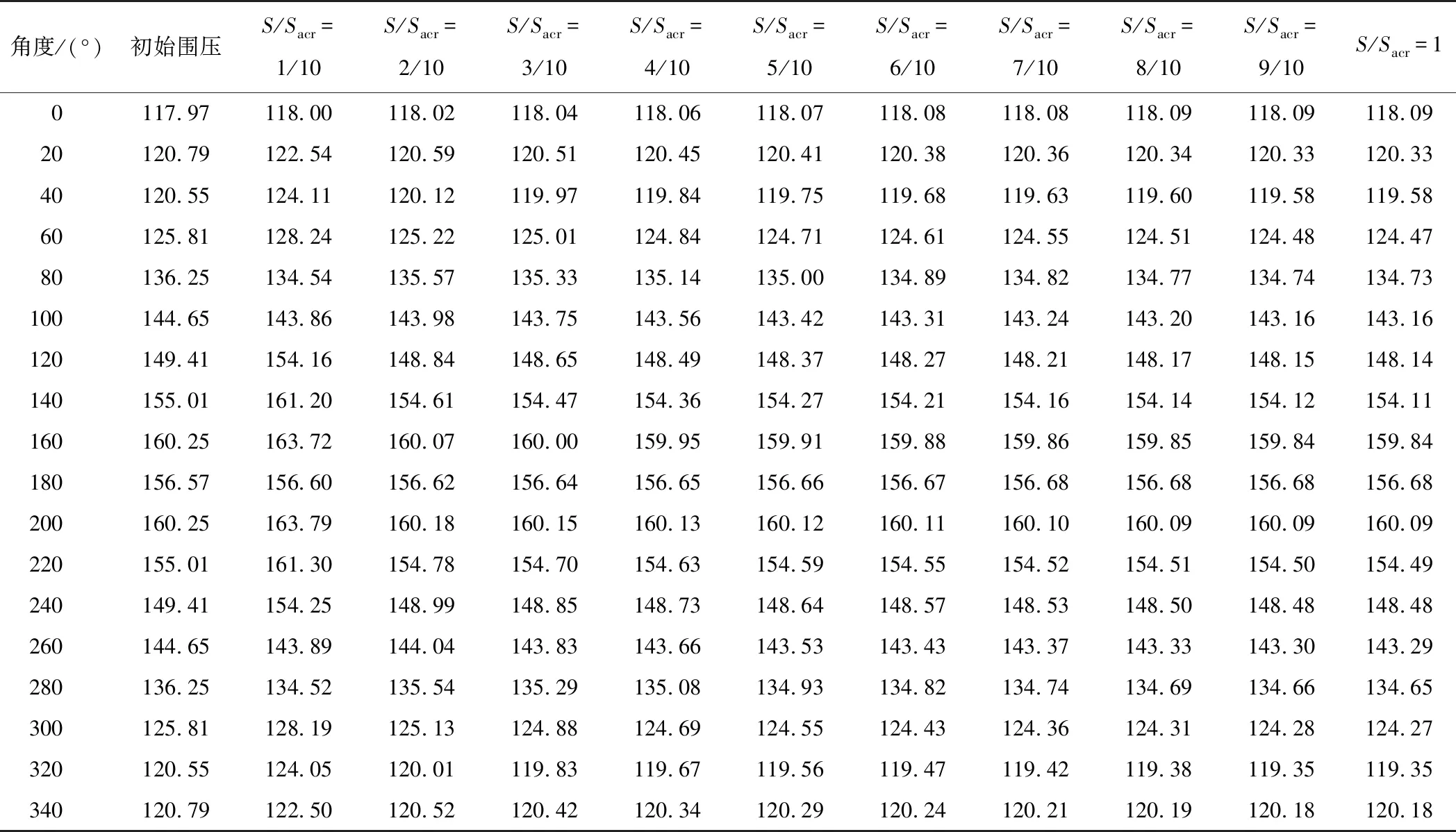
表1 围护结构在不同位移工况下的围压值

2.2 管片结构形式

盾构隧道外径为6.2 m、内径为5.5 m，衬砌环环宽为1.2 m，管片厚度为0.35 m。图6为三环管片平面示意图。由图6可知，管片环由6块管片组成，采用“1+2+3”的分块方式设计。其中： 包含1块封顶块，封顶块处在圆环350°～10°之间，圆心角为20°； 2块邻接块，圆心角为68.75°； 3块标准块，圆心角为67.5°。管片之间采用2根强度为6.8级的M30螺栓进行连接。管片环与环之间采用16根强度为6.8级的M30螺栓进行连接，采用三环通缝拼装。

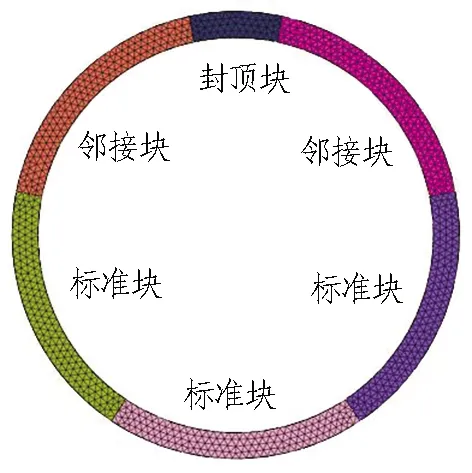
图6 三环管片平面示意图

2.3 数值计算模型

采用MIDAS/GTS NX软件建立数值计算模型，如图7所示。管片环及螺栓均采用尺寸为0.1 m的四面体实体单元进行模拟，管片与管片及管片与螺栓之间通过设置接触面来模拟隧道变形。地层作用在盾构衬砌结构上的抗力，通过在衬砌环全周设置法向地基弹簧单元进行模拟，并将地层抗力与衬砌结构位移之间的关系简化为正比关系，其中的比例因子定义为地基抗力系数。本文的地基抗力系数K=5 000 kN/m3。螺栓和混凝土管片的本构模型均采用范梅塞斯模型进行模拟，计算参数见表2。

图7 数值计算模型示意图

表2 管片混凝土和螺栓模型参数

盾构衬砌环全周的围压处理，采用在模型中将衬砌模型的周边分成18等份，每份角度为20°，并在每一部分加上表1计算得出的围压值。

管片环分为上、中、下3环，管片环与环以及块与块之间存在界面单元，在衬砌环外部设置有地基弹簧单元。在进行有限元模拟时，采用地层弹簧模拟地层抗力。首先,根据修正惯用法算出衬砌环每20°的垂直均布压力，并分块施加在衬砌环上，得到衬砌环在初始围压作用下的受力与变形；再根据文献[17]的方法算出基坑开挖卸载后产生的附加荷载，在初始围压的基础上，施加所算出的附加围压，计算得到最终衬砌环的变形规律。

3 盾构隧道横断面变形规律分析

3.1 隧道衬砌结构横向变形分析

图8为初始围压下隧道衬砌结构收敛云图。由图可知，管片收敛值在初始围压作用下的最大收敛值仅达到1.86 mm，以指向衬砌环外侧为正。在基坑未开挖时隧道仍会产生一定的收敛值，但远不会达到报警值。

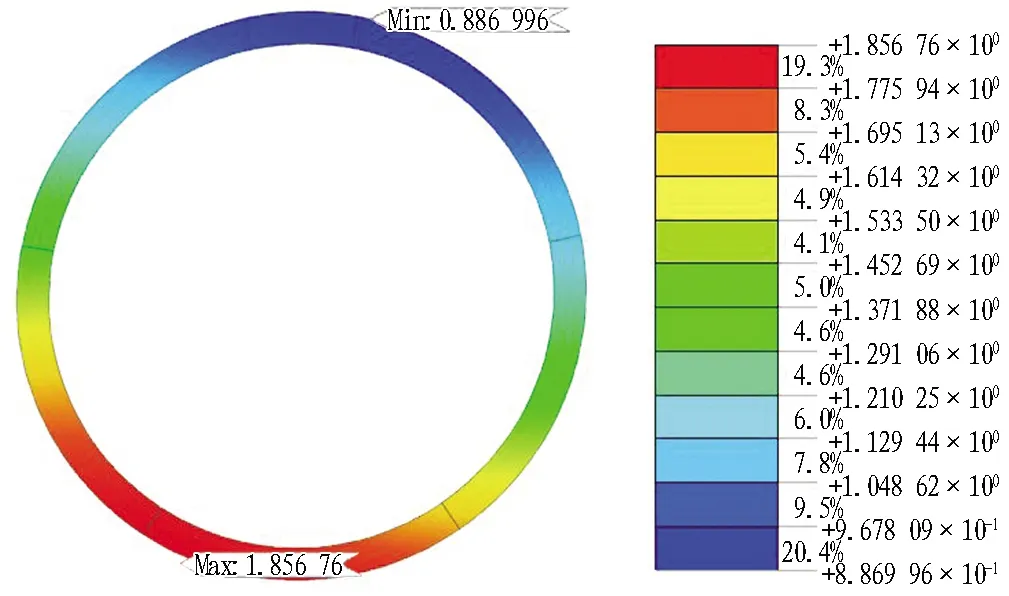
图8 初始围压下隧道衬砌结构收敛云图(单位： mm)

图9为附加围压下隧道衬砌结构收敛云图。由图可知，管片收敛值在基坑开挖过程中变化很大，当偏心卸载产生的附加围压作用在衬砌环上时，其最大收敛值为6 mm，该值与文献[18]中隧道最大收敛值5.5 mm比较接近，证明本文有限元模拟方法的可靠性。

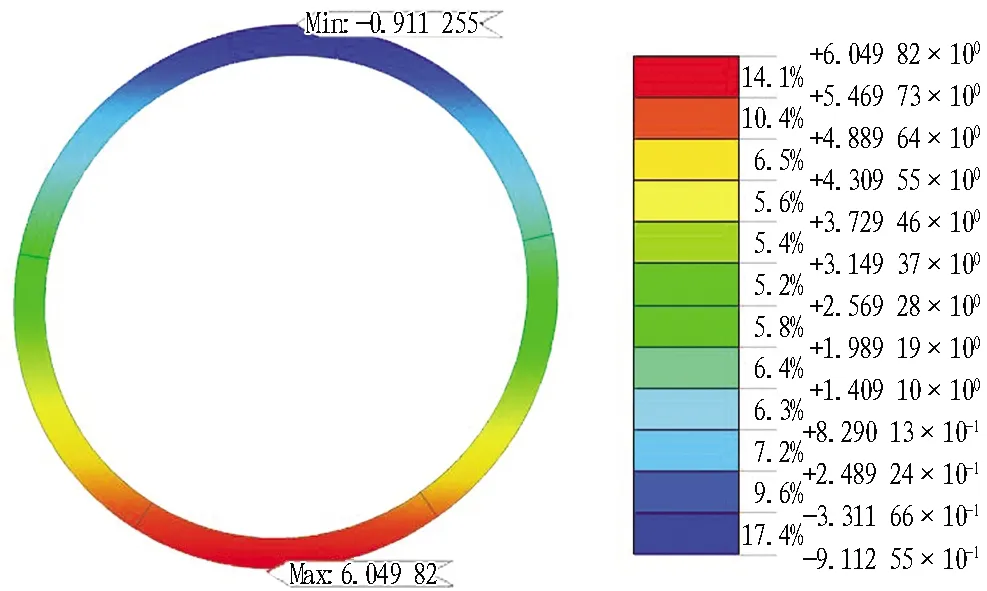
图9 附加围压下隧道衬砌结构收敛云图(单位： mm)

图10为隧道衬砌结构收敛云图。由图可知，隧道衬砌结构整体呈现“斜椭圆”变形，椭圆长轴与水平方向呈45°左右。这是因为在偏心卸载作用下，衬砌结构受到竖向和水平方向的压力，合力方向与垂直方向呈一定的角度，从而产生斜向“压扁”的效果。基坑位于隧道左侧，此时混凝土的最大位移值为9.1 mm。

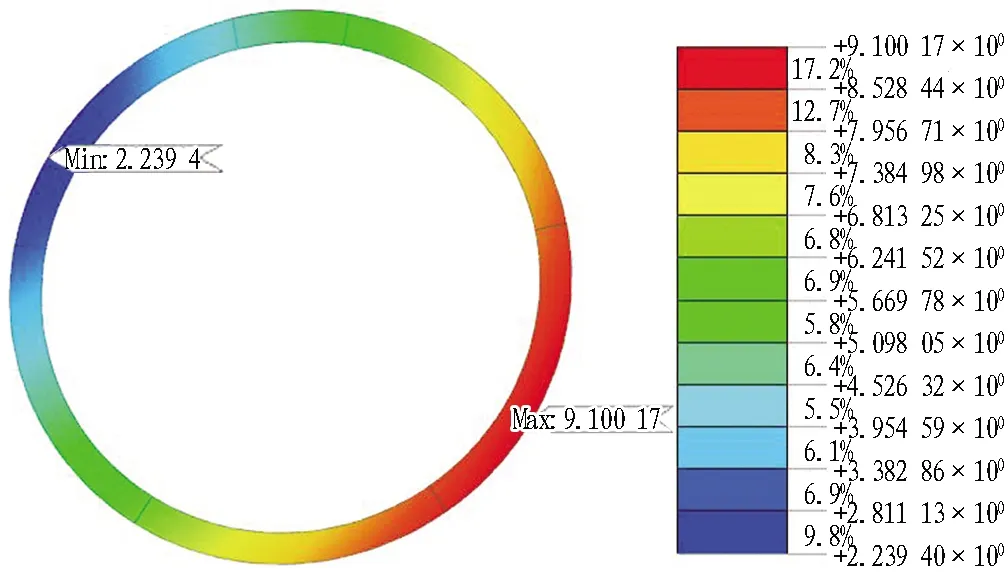
图10 隧道衬砌结构收敛云图(单位： mm)

3.2 隧道衬砌结构内力分析

图11和图12分别为隧道管片结构与螺栓平均应力云图。由于隧道结构发生“斜椭圆”变形，在椭圆长轴两端隧道内侧发生挤压现象，因而混凝土的应力较大。另外，由于应力集中的原因，管片与管片接缝处的应力较大，文献[16]中也得到了类似的结论。混凝土最大应力值为9.6 MPa，发生在邻接块与标准块的接缝处。螺栓最大应力值发生在相邻管片环与管片环之间的环向螺栓，其最大应力值为3.2 MPa。

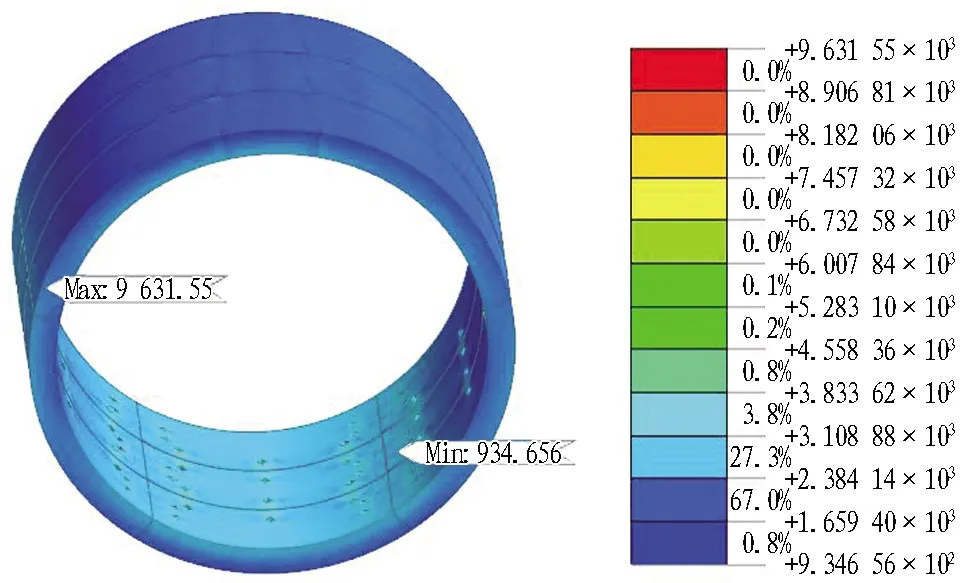
图11 隧道管片结构平均应力云图(单位： kN/m2)

4 横断面变形控制限值

4.1 评价指标的选取

目前旁侧基坑开挖大都属于偏心卸载，且在隧道拱腰处变化较为明显。图13为“斜椭圆”变形示意图。隧道在偏心卸载情况下，由于隧道横截面发生“斜椭圆”变形，椭圆的长轴与水平线呈一定的角度，将会发生横向直径变化不大甚至没有变化，但隧道横截面发生巨大变形的现象。

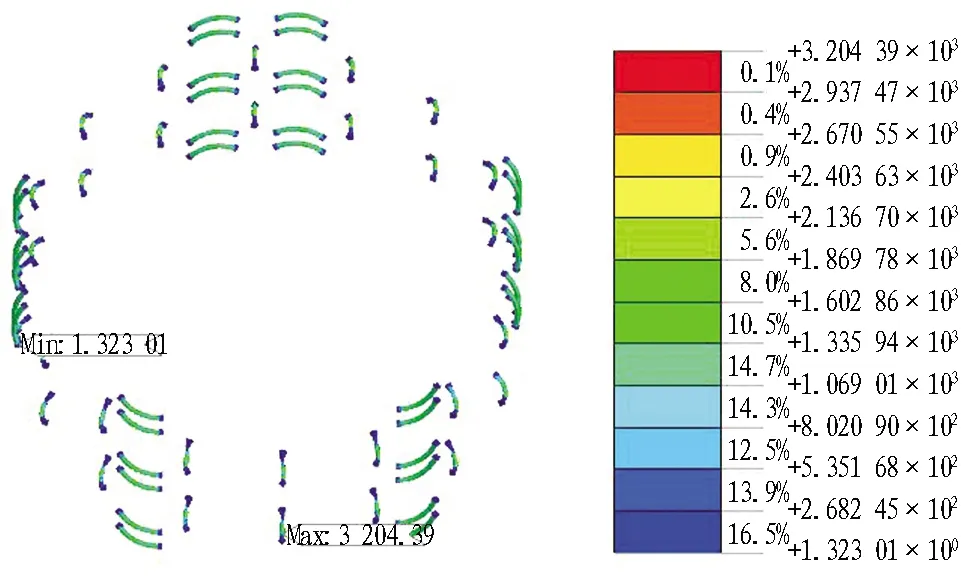
图12 螺栓平均应力云图(单位： kN/m2)

图13 “斜椭圆”变形示意图

现有研究大多采用直径变化量作为隧道横截面变形的评价指标，但皆适用于对称卸载情况。实际过程中隧道会产生“斜椭圆”变形。因此，本文采用椭圆度作为安全评价指标，其计算公式为：

T=2(a-b)/D。

式中：a为隧道长半轴；b为隧道短半轴；D为隧道外径。

4.2 偏心卸载工况下三维有限元计算

设计偏心卸载工况，围护结构位移S=7.2 m，计算初始围压以及S/Sacr=1/10(β=4.7%)、2/10(β=8.5%)、3/10(β=11.5%)…8/10(β=18.6%)9种工况下隧道的围压值，在有限元模型上添加围压并进行模拟计算。

根据地铁相关设计、验收规范及相关经验，地铁隧道椭圆度超过25‰的管片需要进行钢板内支撑加固[20]。图14为围护结构相对位移量与隧道椭圆度关系。由图可知, 在初始围压作用下的椭圆度仅为3.26‰，远远未达到需要加固的状态，但随着基坑开挖偏心卸载导致β增大，隧道的椭圆度也逐渐增大，当S/Sacr=2/10(β=8.5%)时，椭圆度达到28.13‰，超过允许范围值[20]；当S/Sacr≥4/10时，椭圆度的增长速率会逐渐降低，椭圆度值开始趋于稳定。因此，在基坑开挖过程中要严格控制围护结构位移量，以保证隧道的安全。

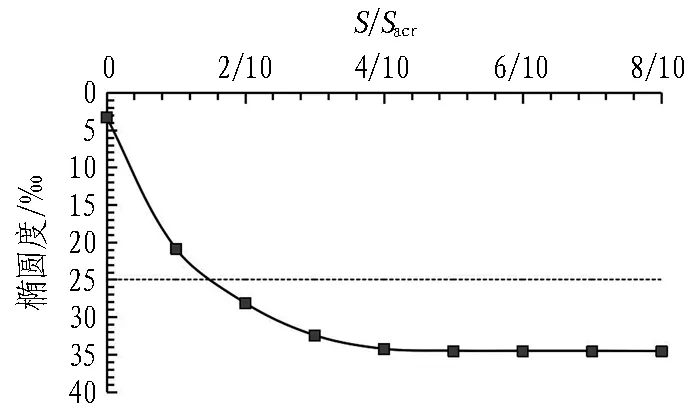
图14 围护结构相对位移量与隧道椭圆度关系

图15为偏心卸载工况下围护结构相对位移量与管片最大位移关系，图16为隧道椭圆度与管片最大位移关系。由图15—16可知，在基坑未开挖前管片最大位移值仅为2.23 mm，此时椭圆度为3.26‰；当S/Sacr=2/10(β=8.5%)时，混凝土最大位移值开始稳定，并趋于稳定值9.2 mm，此时混凝土最大位移稳定值所对应的椭圆度达到28.13‰。这是由于基坑开挖会对隧道产生偏心卸载，使隧道受到指向基坑侧方向的力，管片会产生相应的位移。

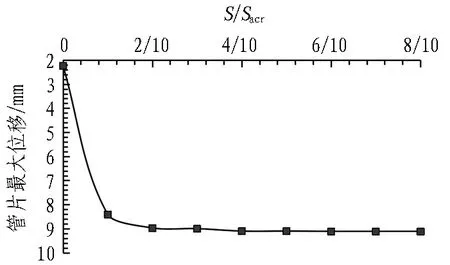
图15 围护结构相对位移量与管片最大位移关系

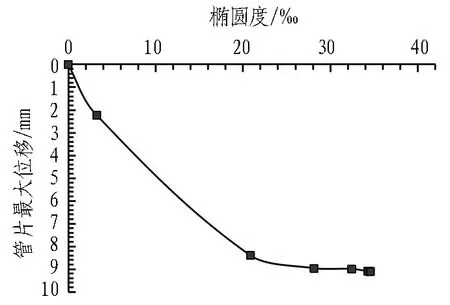
图16 隧道椭圆度与管片最大位移关系

图17和图18分别为偏心卸载工况下隧道椭圆度与混凝土和螺栓最大应力之间的关系。可以看出，当椭圆度为28.13‰时，S/Sacr=2/10(β=8.5%)，混凝土以及螺栓最大应力值趋于稳定，隧道由于基坑开挖卸载呈现“斜椭圆”变形，长轴端处于标准块和邻接块的接头处，降低了隧道的承受能力；当椭圆度大于28.13‰时，混凝土最大应力值达到9.7 MPa。在图18中，螺栓最大应力值同样随着椭圆度的增大而增大，当椭圆度大于28.13‰时，螺栓最大应力值趋于稳定值3.2 MPa。

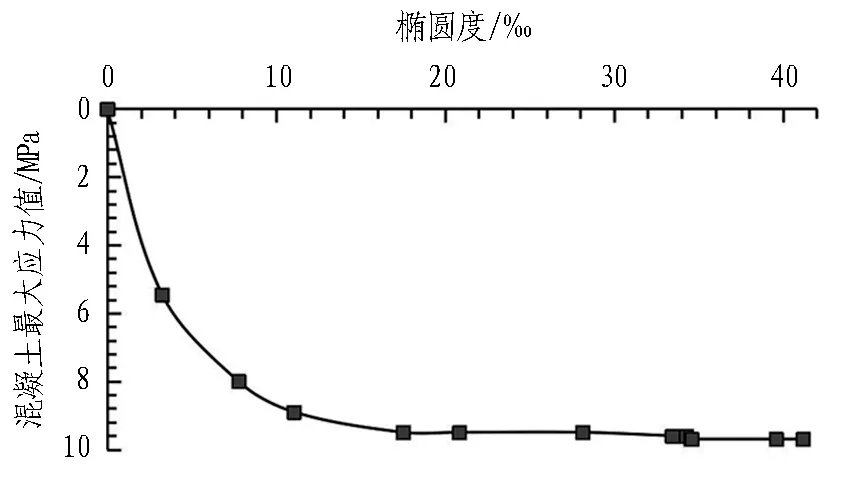
图17 隧道椭圆度与混凝土最大应力关系

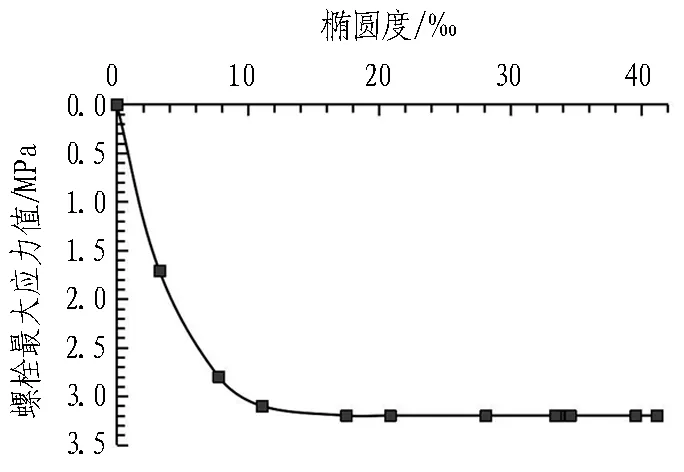
图18 隧道椭圆度与螺栓最大应力关系

4.3 横向变形控制限值

结合文献[19]的方法，计算得出当围护结构实际位移与极限位移之比为1/10时，管片最大位移为8 mm，此时对应的β为4.7%，椭圆度为20.84‰，隧道处在安全范围；但当围护结构实际位移与极限位移之比为2/10时，管片最大位移值接近10 mm，对应的β为8.5%，椭圆度达到28.13‰，超过规定范围值25%[20]，需要进行钢板内支撑加固，此时对应的混凝土最大应力值为9.5 MPa，螺栓最大应力值为3.2 MPa。

5 结论与讨论

1)有限元分析结果表明，基坑开挖卸载会导致隧道呈“斜椭圆”变形，由于应力集中的原因，此时管片收敛值最大处发生在邻接块与标准块的接缝处，通过与实测数据相对比，进一步验证了该方法的正确性。

2)基坑开挖初期会导致β值增长速率过快，会产生较大的附加荷载，此时椭圆度变化较大。椭圆度会随着围护结构的位移增大而增加，隧道衬砌结构会由于基坑开挖偏心卸载产生较大的收敛变形。β值增大到一定值时，随着β值增长速率减慢而导致隧道所受到附加荷载减少，椭圆度增长速率会逐渐降低，隧道最大水平位移增长速率也逐渐减少，此时衬砌结构收敛值趋向稳定，随着围护结构位移达到极限值，此时椭圆度会再度增大。因此，基坑开挖过程中要严格控制β值在合理范围之内，确保盾构隧道安全。

3)相对于以往学者采用地层-结构法模拟基坑开挖对隧道的影响，本文采用荷载-结构法来模拟基坑开挖对隧道的影响，通过采用弹簧模拟土体，大量简化网格单元，进行精细化模拟。通过计算真实情况下隧道表面受到的荷载(围压)，算出隧道在实际工况中的非对称荷载，采用围压来代替实际工程中隧道所受到的水土压力，可以直观地分析实际基坑开挖偏心卸载过程中隧道所受到的荷载。

本文三环管片模型可以为大型通缝足尺管片试验提供参考，进一步预测基坑开挖对隧道衬砌结构的影响，但本文三环管片模型并未考虑止水带、手孔等，且忽略了螺栓孔与螺栓孔之间的相互作用，因此，本文模型需要作进一步研究。