基于ADAMS的全断面硬岩隧道掘进机主机耦合振动分析

王旭龙， 朱 晔

(1. 大连交通大学机械工程学院， 辽宁 大连 116028； 2. 天津职业技术师范大学汽车与交通学院， 天津 300222)

0 引言

全断面硬岩隧道掘进机(简称TBM)是一种集掘进、出碴、导向、支护和通风防尘等多功能为一体的大型流水线式高效隧道施工机械，广泛应用于城市地铁工程、引水工程、跨江隧道工程、跨山铁路和公路隧道工程、市政管廊工程[1-2]。TBM掘进过程中常常面临极端硬岩涌水、破碎带等复杂的地质环境，导致设备的工作环境恶劣，岩石破碎产生的滚刀强冲击载荷传递到主机，会引发主机系统关键结构的剧烈振动[3]，进而引起TBM关键系统的损伤，导致隧道工程建设工期延长，严重的甚至导致TBM整机与施工隧道报废，因此，有必要对TBM主机系统进行振动分析。

目前，国内外学者主要对TBM局部子系统的动力学进行了详细分析，例如国内很多高校分别针对TBM的刀盘刀具系统、主驱动系统、推进系统等方面建立了相应的动力学模型，并进行了相应的现场实测。文献[4-6]针对TBM的滚刀系统、驱动系统分别构建了滚刀系统、主驱动系统的非线性动力学模型，研究了螺栓预紧力、结合面刚度等对滚刀响应的影响和内外部激励对主驱动各个关键结构振动的影响。文献[7]建立了TBM刀盘系统动力学分析模型，并探究了刀盘分体质量、刀盘转速、齿轮布置参数等因素对刀盘振动特性的影响。文献[8-11]对TBM滚刀的破岩载荷进行了深入的研究，基于搭建的试验台对破岩模型进行了验证。文献[12]提出了盾构隧道掘进机刀盘驱动系统的一般非线性时变动态模型和线性时变动态模型。文献[13]建立了有限元模型，通过引入非线性弹簧元件来模拟滚刀与岩石之间的相互作用，从而对掘进过程进行动态模拟，针对不同的岩层，获得了确保刀盘动力稳定性的关键驱动速度。文献[14]考虑到多小齿轮传动中周期性变化的啮合刚度以及变频电动机驱动器的速度-转矩特性，建立了隧道掘进机旋转系统的动力学模型，比较了几种典型混合面条件下TBM隧道的动态开挖转矩和刀盘转速。国外对TBM的研究主要侧向于工程应用，文献[15]基于300多个TBM项目记录的数据库开发了一种新模型来提高穿破岩率估算的准确性。文献[16]对不同硬岩TBM挖掘项目的性能数据库进行了编译和分析，开发了新的TBM性能预测模型。文献[17]等利用Lotschberg Base隧道的现场穿透指数(FPI)分析了岩体条件与TBM性能之间的关系。

综上所述，前人在TBM动力学方面的理论研究主要集中在局部子系统，通过建立理论计算模型对各个子系统进行较为详细的分析，但是各个子系统考虑的参数较多，往往导致分析模型复杂，计算效率低，忽略了各个局部子系统间的相互影响。因此，本文首先对TBM主机各个子系统进行简化，基于Adams软件，对TBM主机各个关键节点进行划分，考虑各子系统间的连接方式，通过理论计算各个连接刚度和阻尼、各油缸刚度和阻尼，建立TBM主机系统的动力学模型。然后通过对TBM工况进行分析，建立3种典型的TBM刀盘载荷加载方式，并分别对3种载荷作用下的TBM振动分析模型进行求解，对主机系统各关键部件进行时域、频域的振动响应分析，将理论分析结果与前人的研究数据进行对比，验证仿真计算的正确性，最后得出主机系统振动的传递规律。

1 TBM主机系统动力学模型

1.1 TBM主机的组成

TBM主机系统包括4大系统： 刀盘刀具系统、支护系统、主驱动系统和推进系统。其中，刀盘刀具系统由盘形滚刀、刀座、刀盘结构和刮碴板组成，主要作用是维持掌子面、破岩和刮碴；支护系统由底座、护盾、机头架、支护油缸等组成，主要起到支撑岩壁、防止岩石崩塌的作用；主驱动系统由电机、减速器、小齿轮、大齿圈等组成，主要作用是驱动刀盘转动；推进系统由推进液压缸、主梁、撑靴、鞍架、尾撑等组成，主要起到推动刀盘向前运动的作用。TBM主机结构图如图1所示。

图1 TBM主机结构

1.2 TBM的工作原理[18]

TBM掘进时，首先，撑靴内侧可横向伸缩的液压油缸伸出，使撑靴固定在已经挖掘好的隧道内壁上； 其次，推进油缸以撑靴为支撑，推动主机系统(包括主梁、机头架、护盾、刀盘)前进，这时滚刀压入掌子面(刀盘接触的岩石面)； 然后，驱动电机带动刀盘旋转，滚刀滚动，从掌子面切削岩石； 最后，由于重力，岩碴掉落在刀盘和掌子面中间，刮碴板在最低端将岩碴铲起，岩碴随着溜碴板一起运动，随着刀盘旋转，溜碴板逐渐向下倾斜，岩碴向下落入漏斗中，经皮带输送机传送到隧道外。推进油缸达到最大行程时，刀盘停止转动，撑靴内侧油缸收缩，撑靴离开岩壁，在辅助油缸的作用下，撑靴向前移动，至此完成一次掘进循环。护盾撑在隧道内壁上，保持设备稳定，降低掘进过程的振动，进而减少刀具磨损。掘进机上方的顶护盾一般装有向后延伸的指形护盾，可保护掘进机不受崩落岩石的损坏。

1.3 TBM主机系统动力学模型

综合考虑TBM主机系统中各个子结构的功能和特点，对主机系统的结构进行重新划分，建立简化的TBM主机三维模型。对建立的TBM主机系统的结构以及结构间的连接进行等效，并建立相应的刚度和阻尼计算方法。最后将建立的三维模型导入到Adams中，根据TBM的实际工况对约束和载荷进行设置，并根据理论计算模型对连接刚度和阻尼进行设置。基于Adams, 建立TBM主机系统等效动力学模型，如图2所示。

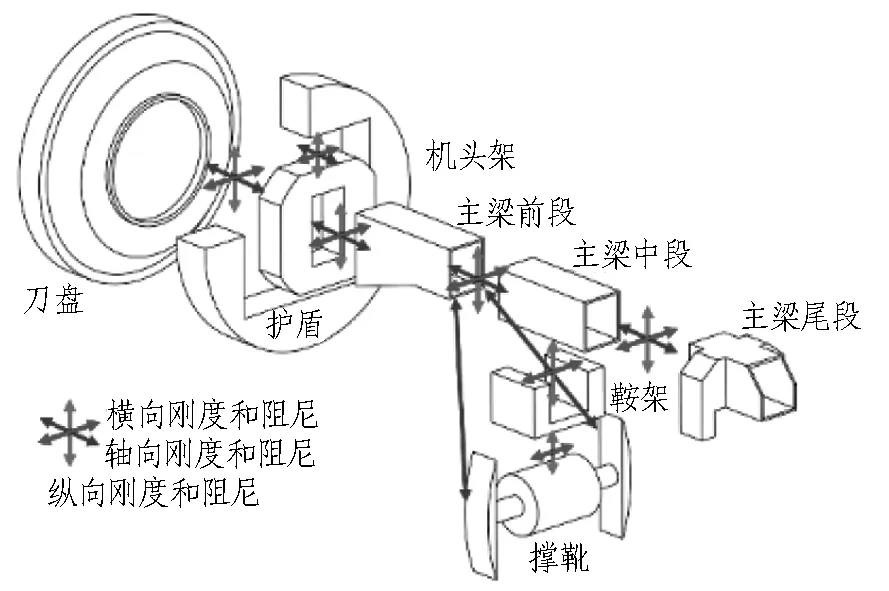
图2 TBM主机系统等效动力学模型

1)将刚度等效为结构件本身刚度与连接刚度的串联，阻尼等效为两者的并联；

2)刀盘和机头架通过主轴承连接，将刀盘等效为1个零件，主轴承等效为1个零件，主轴承与刀盘固定连接，刀盘和机头架之间的相对振动有3个方向，3个方向的刚度分别等效为各自方向刀盘的结构刚度、主轴承的结构刚度和主轴承相应方向的非线性刚度的串联，阻尼为相关方向3个阻尼的并联；

3)机头架和护盾通过多组油缸连接，纵向的连接刚度分别等效为护盾的结构刚度与连接油缸的非线性刚度的串联，阻尼为各个方向阻尼的并联，护盾与岩壁固定约束；

4)机头架和主梁前段通过螺栓连接，3个方向的刚度分别为相应方向机头架结构刚度和螺栓连接刚度的串联，阻尼为相应方向2个阻尼的并联；

5)主梁前段和主梁中段通过螺栓连接，3个方向的刚度分别为相应方向主梁前段结构刚度和连接刚度的串联，阻尼为相应方向2个阻尼的并联；

6)主梁前段和撑靴通过主推油缸连接，主推油缸等效为非线性的弹簧和阻尼，刚度为主梁刚度和油缸的非线性刚度串联，阻尼为2个阻尼的并联；

7)主梁中段与鞍架轴向为移动连接；

8)撑靴与岩壁为固定连接。

1.4 滚刀载荷

TBM掘进时，撑靴固定，主推油缸向前推进，滚刀压入岩石，同时电机驱动刀盘旋转，此时滚刀挤压剪切岩石，岩石的脆性断裂导致滚刀的冲击振动，通过滚刀刀座，多把滚刀的振动在刀盘进行耦合，引起刀盘横向、纵向、轴向的剧烈振动，直至传递到设备的最终端，因此滚刀破岩载荷对TBM主机系统的振动分析至关重要。基于WORKBENCH软件,对滚刀破岩过程进行仿真，得到单把滚刀的垂直破岩载荷，最后将滚刀载荷作为外部载荷加载在相应位置的滚刀上，如图3所示。侧向力和滚动力分别是轴向力的0.15和0.1倍，α为滚刀的安装角度。

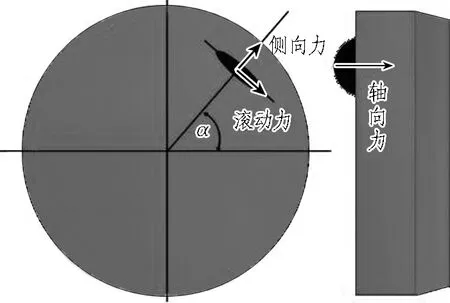
图3 滚刀载荷

1.5 TBM典型工况与刀盘载荷

根据掘进路线变化，将TBM的典型掘进工况分为直线掘进和转弯掘进2种工况，如图4所示。在直线掘进工况下，由于地理环境多变，TBM面临不同的岩层，有均匀地质，有不均匀地质。因此，根据TBM施工特点与实际地质情况，常见的刀盘载荷工况可分为全推力、上软下硬和转弯3种，如图5所示。

(a) 直线掘进工况

(b) 转弯掘进工况

在全推力载荷下，如图5(a)所示，TBM在均匀地质下沿直线掘进，由于滚刀贯入度相同，所有滚刀均承受最大载荷；在上软下硬载荷下，如图5(b)所示，滚刀贯入度相同，但是不同的岩层载荷大小不一，刀盘一半的滚刀载荷为最大，另一半载荷为最大载荷的一半；在转弯载荷下，如图5(c)所示，刀盘与掌子面成一定角度，此时仅部分滚刀破岩，设置刀盘边缘1/3滚刀载荷为最大，其他滚刀载荷为0。

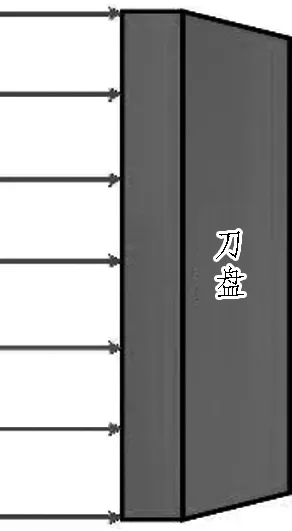
(a) 全推力

(b) 上软下硬

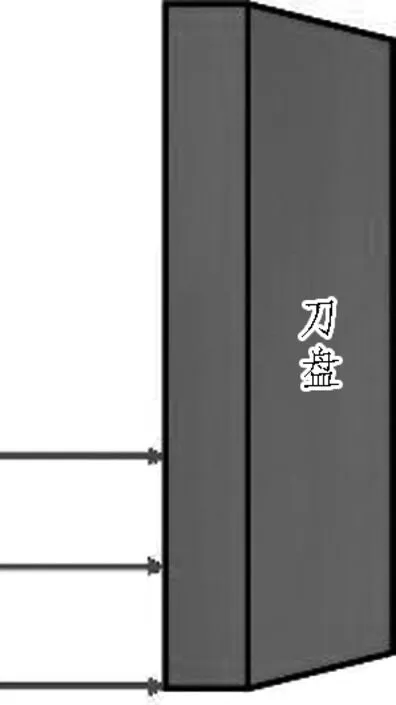
(c) 转弯

1.6 主机系统刚度和阻尼的确定

1.6.1 齿轮接触力

在齿轮啮合过程中，啮合点的受力主要有法向接触力和切向接触力，采用冲击函数法得到齿轮法向接触力，采用库仑摩擦法得到切向接触力。

齿轮接触过程等效为与穿透深度有关的非线性弹簧阻尼模型，齿轮法向接触力Fn主要由齿轮切入带来的弹性力和齿轮相对速度引起的阻尼力组成，其计算公式为

(1)

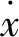
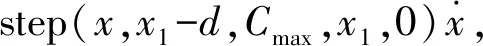
(2)

式中：i=h1-h0；j=(x-x0)/(x1-x0)。

利用库仑摩擦法得到齿轮啮合产生的切向接触力，接触力大小与接触正压力成正比，方向与相对移动速度相反，表达式为

Fs=-Fn×step(vt,-vs,-1,vs,1)×step(ABS(vt),vs,fst,vd,fdy)。

(3)

式中：Fs为切向接触力；Fn为法向接触力；vt为齿轮相对移动速度；vs为最大静摩擦对应的相对移动速度；vd为动摩擦相对移动速度；fst为静摩擦因数；fdy为动摩擦因数。

由赫兹接触理论得出接触刚度计算公式

(4)

式中：R1、R2为两齿轮啮合处的曲率半径；h1、h2为材料参数。

hi=(1-vi2)/(πEi)，i=1,2。

(5)

式中：v1、v2为两齿轮的泊松比；E1、E2为两齿轮的弹性模量。

结合经验及仿真实验数据，取弹簧力指数e为1.5； 阻尼系数一般取刚度系数的0.1%～1%； 结合齿轮参数信息取齿轮的法向接触深度δ值为0.1 mm； 依据齿轮材料特点，取动摩擦因数为0.05，静摩擦因数为0.08。

1.6.2 液压油缸的刚度和阻尼

液压油缸主要由活塞杆、缸筒和液压油等组成。液压油缸的刚度为非线性的，由液压油的刚度、刚体的刚度和活塞杆刚度组成。活塞杆的刚度可以通过有限元分析求取，在杆的一端添加固定约束，另一端通过施加单位载荷得到对应的变形，之后通过胡克定律求出刚度，阻尼采用经验公式计算。

液压油的刚度可表示为

(6)

式中：β为液压油有效体积弹性模量；A为活塞面积；V为封闭容器内的液压油体积。

(7)

式中：c为结构体的阻尼；ξ为阻尼比，取0.025；me为结构件的质量；ke为结构件的刚度。

1.6.3 轴承的等效刚度和阻尼

主轴承在TBM中是一个重要的支撑部件，和传统的轴承一样，主要由内外圈、保持架和滚子等组成。主轴承由3部分组成，为主推轴承、反推轴承以及径向轴承。主推轴承主要承担掘进过程中的主推力，反推轴承的作用是约束轴向位移，同时承担反推力，径向轴承的作用是承担刀盘驱动系统的质量。轴承是向心推力轴承，其轴向刚度计算式为

(8)

式中：Ka为轴承轴向刚度；n为刚度系数，取1.1；Z为滚子个数；α为滚子轴承接触角，取值90°；δa为轴承轴向位移；le为滚子的有效接触长度；Dw为滚子有效直径；Fa为轴向载荷。

轴承径向刚度计算公式

(9)

式中：δr为轴承径向位移；φi为滚子对应的位置角；Fr为纯径向载荷。

1.6.4 关键节点的结构刚度和阻尼

关键节点的等效刚度运用有限元分析的方法计算，并采用经验公式计算阻尼。

1.7 主机各部件质量

见表1。

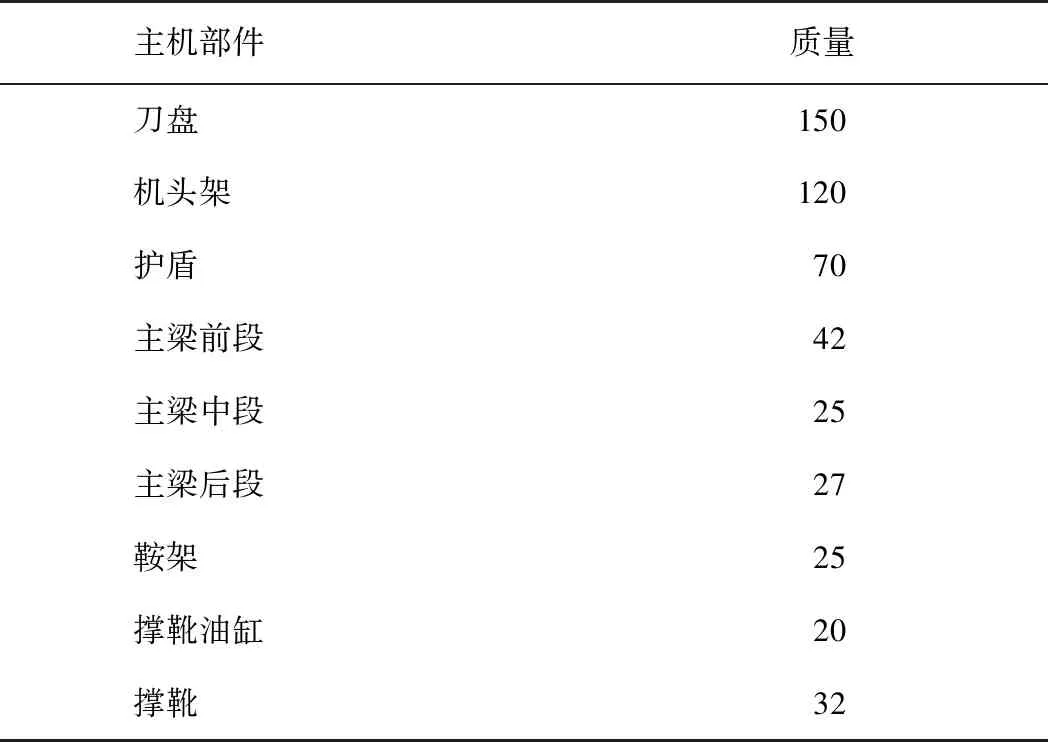
表1 主机各部件质量

2 TBM主机系统动力学分析

针对建立的动力学分析模型，采用Adams进行求解后，对TBM主机系统的时域、频域振动响应进行分析，从而得到TBM关键部件振动响应情况。

2.1 主机关键结构刚度和阻尼

根据上节主机系统刚度和阻尼的确定可知，主机系统关键部件等效刚度、等效阻尼如表2—3所示。

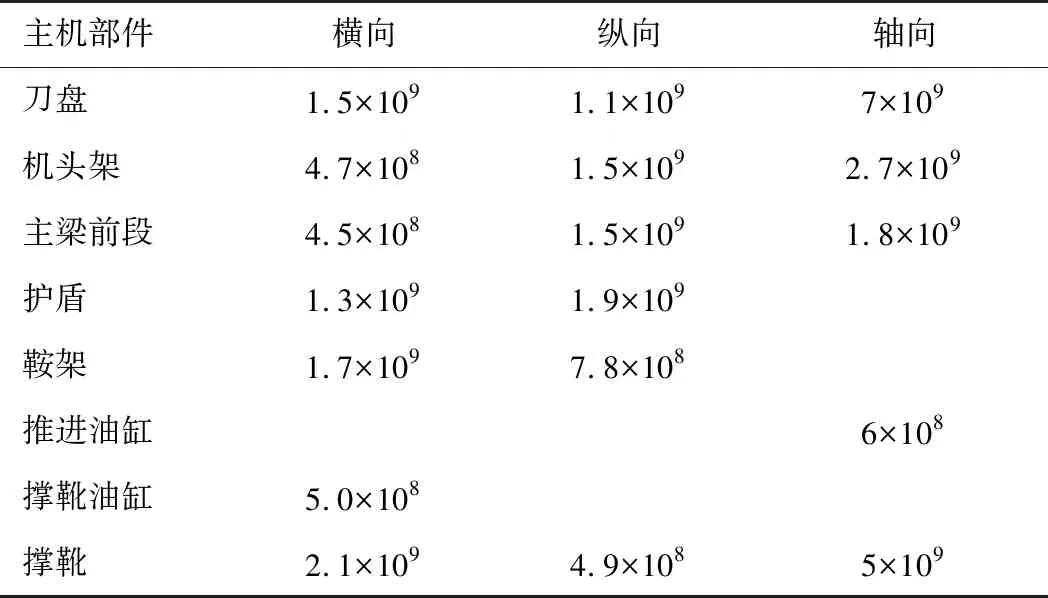
表2 主机系统关键部件等效刚度

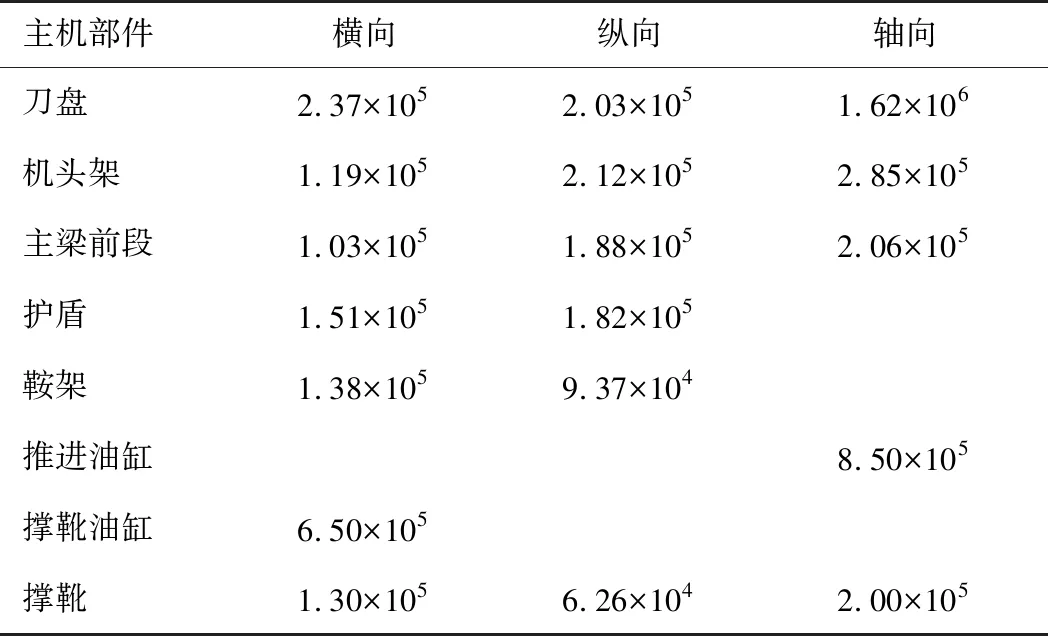
表3 主机系统关键部件等效阻尼

2.2 全推力下主机关键结构的动态响应

将表1—3所示的参数带入动力学模型进行动力学分析求解，刀盘的转速为6 r/min(即每10 s刀盘转1圈)，因此待系统运行稳定后，提取10 s的刀盘、机头架、主梁前段的三向加速度振动数据,TBM关键部件的时域响应如图6所示(蓝色为轴向振动加速度，绿色为横向振动加速度，红色为纵向振动加速度)。

图6(a)为刀盘的三向加速度，刀盘的三向加速度中轴向振动最大，最大值约为2.5g；横向的振动加速度次之，最大值约为2.2g；纵向的振动加速度最小，最大值约为2.0g。图6(b)为机头架的三向加速度，和刀盘的振动相似，机头架的轴向振动最大，横向和纵向的振动幅值相差不大，均小于轴向振幅，其中轴向加速度的最大幅值约为2.3g，横向加速度的最大幅值约为1.9g，纵向加速度的最大振幅约为1.8g。相较于刀盘和机头架，图6(c)主梁前段的三向加速度的振动幅值有明显的下降，其轴向加速度的最大振幅约为1.3g，横向振动加速度的最大幅值为1.2g左右，纵向加速度的最大幅值约为0.9g。这与文献[5]得到的实测结果和分析结果相近，因此，证明分析是正确的。

(a) 刀盘三向加速度

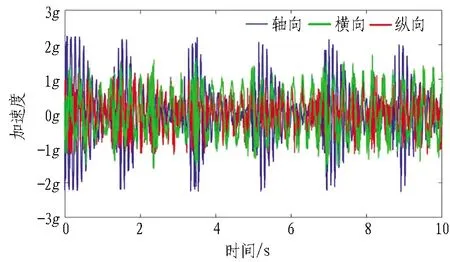
(b) 机头架三向加速度

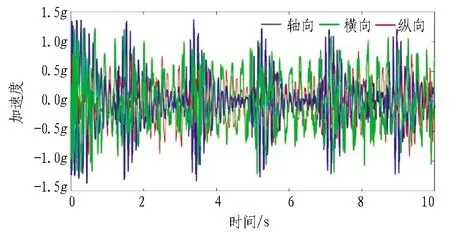
(c) 主梁前段三向加速度

2.3 频域分析

对主机关键部件的振动加速度进行频域分析，TBM关键部件轴向和横向频域响应如图7所示。

通过对主机系统轴向和横向的振动加速度响应的频谱分析可知： 在激励作用下，主机各个关键部件的轴向振动主要是低频振动，在5 Hz左右出现最大振幅，在100 Hz左右出现另一个最大振幅。同时由于齿轮耦合作用，在横向振动的频域上，由于机头架受到齿轮啮合振动的影响，机头架的横向振动在150 Hz左右的频域上出现了一个较大的振幅区间，刀盘和主梁受到齿轮啮合引起振动的影响较小。

典型工况下主机关键结构振动响应见图8。由图8(a)可知，上软下硬工况下，刀盘的轴向振动加速度最大均为1.5g，机头架的振动加速度约为0.9g；图8(b)转弯纠偏工况下，刀盘和机头架轴向加速度幅值基本接近，都较小，约为0.4g。

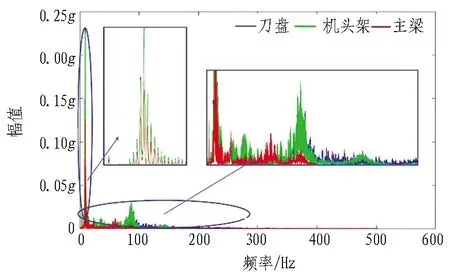
(a) 轴向频域响应

(b) 横向频域响应

(a) 上软下硬条件下关键结构轴向振动响应

(b) 转弯条件下关键结构轴向振动响应

3 结论与讨论

1)在全推力工况下，TBM主机中刀盘的振动最为剧烈，沿着刀盘到机头架，振动逐渐衰减。3个方向上，各部件的轴向振动最为剧烈，沿着刀盘到主梁，各个关键结构在3个方向的振动衰减规律基本一致，分别衰减了约25%和55%。每个结构的轴向振动约为横向和纵向振动的1.75倍。刀盘、机头架、主梁前段轴向振动主要是0～10 Hz的低频受迫振动。机头架因为受到齿轮啮合的耦合振动影响，在150 Hz左右存在耦合振动。

2)和全推力工况相比较，在上软下硬和转弯工况下，刀盘和机头架的轴向振动都有一定的减小，其中上软下硬工况下，刀盘的轴向加速度减小约40%。转弯工况下，刀盘的轴向加速度减小约80%，这与刀盘的载荷减小比例存在一定的关系。

3)建立的TBM主机动力学模型可以作为设备运行的指导依据，驾驶员可以根据设备的振动情况和相应的工况对设备的掘进载荷进行控制，保证设备在安全的范围内工作，延长设备的寿命。本文尚未考虑电机主从控制策略和刀盘倾覆振动，后续将进行进一步的研究。