多因素下大断面矩形顶管施工对地层竖向变形影响研究

周 浩， 马保松， 赵阳森， 张 鹏

(1. 中国地质大学工程学院， 湖北 武汉 430074； 2. 中山大学土木工程学院， 广东 珠海 519082)

0 引言

随着国家社会经济的高速发展，城市地下空间开发愈发重要，顶管技术作为非开挖技术的一种，施工时对周围环境及建筑影响较小[1-2]。目前大断面、长距离及复杂地层顶进的矩形顶管技术逐渐成为发展主流[3]，正被广泛应用于地下人行通道、地铁站出入口、地下车行道以及城市综合管廊等工程[4]。相比于圆形顶管，大断面矩形顶管技术主要被运用于交通繁忙、环境复杂的市政建设，其施工影响范围无法精准预测，施工造成的地层变形过大时会造成道路塌陷、建筑物变形等不良影响，所以有必要对其施工引起的地表变形进行研究。

目前矩形顶管施工引起的土体变形计算方法有以下几种： 经验公式法[5-6]、理论计算法[7-9]、数值分析法[10-11]、模型试验法[12-13]等。其中，理论计算经典方法有： 源汇法[7]、随机介质法[8]、弹性力学Mindlin解法[9]。魏纲等[14]基于弹性力学的 Mindlin解，研究类矩形盾构的正面附加推力、管土侧摩阻力、附加注浆压力和土体损失引起的土体竖向位移，以及各因素的影响。韩煊[15]假定隧道收敛不均匀，给出不同断面形式顶管不均匀收敛下的地表沉降公式。许有俊等[16]以 Mindlin 解为理论基础，探究矩形顶管施工过程中地层参数、管节参数、施工参数对地层沉降与隆起的影响。王日东[17]基于随机介质理论探究矩形顶管施工引起的三维土体变形计算方法。综上所述，目前国内外对矩形顶管施工引起的土体变形计算方法较多，但对大断面矩形顶管注浆填充引起的土体变形模式和计算方法较少，而实际工程中注浆填充作为顶管工程的关键工序可有效补偿地层损失，因此，有必要对包含注浆在内的多因素下大断面矩形顶管施工扰动引起的地层竖向变形特性进行系统研究。

本文依托苏州市城北路综合管廊矩形顶管项目，基于弹性力学的 Mindlin解和随机介质理论，结合现场实测数据与Matlab数值分析，根据实测值与计算值的对比分析，探究大断面矩形顶管施工引起的地层竖向变形规律。

1 理论计算模型的建立与假定

矩形顶管在土体中顶进时，受力模型如图1所示。图中：p为正面附加应力，kPa；ft为顶管机头顶部与土体摩擦力，kPa；fr为顶管右侧面与土体摩擦力，kPa；ft′为管节顶面与土体摩擦力，kPa ；fr′为管节右侧面与土体摩擦力，kPa；q为附加注浆压力，kPa；l为顶管机头长度，m；l1为后续管节长度，m；A为顶管水平方向长度，m；B为顶管竖向方向长度，m 。

图1 力学模型简图

假定： 1)土体不排水、不压缩，为各向同性线弹性半无限体；

2)顶进过程中，顶管始终水平，不考虑顶管偏斜等姿态变化；

3)只考虑顶管施工过程中引起的地层变形，土体固结和泥浆固结不计算在内；

4)管土接触面上摩擦力为均布荷载；

5)开挖面为荷载作用面，近似为矩形均布荷载；

6)顶管顶进仅为空间位置上的变化，不考虑时间效应。

1.1 正面附加应力引起土体变形计算

(1)

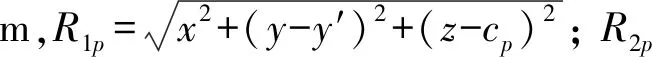
1.2 摩阻力引起的土体变形

(2)

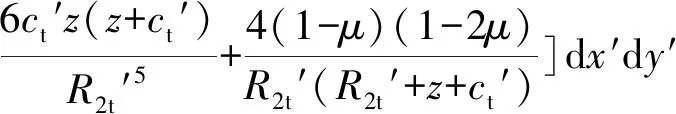
(3)

考虑到管节与顶管环空间隙通常为2～5 cm，故为方便计算，以上3个公式中ct′=ct,R1t′=R1t,R2t′=R2t。

修改x′方向积分区域[-l,0]至[-l-l1, -l]，左右侧面时y′方向积分区域[-0.5A,0.5A] 修改为-0.5A或0.5A，底面时z′方向由-0.5B修改为0.5B，可依次求出矩形顶管管节与顶管各个侧面摩阻力引起的土体竖直方向位移：

w2=wt+wt′+wb+wb′+wl+wl′+wr+wr′

。

(4)

式中：wt、wb、wl、wr分别为顶管上下左右侧面摩阻力造成的土体竖向位移，m；wt′、wb′、wl′、wr′分别为管节上下左右侧面摩阻力造成的土体竖向位移，m。

1.3 地层损失引起的地表土体竖向变形计算

随机介质理论将土体视为一种随机介质，顶管开挖引起的地面沉降则可视为若干个单元体引起地面变形的总和。距离地表深度l′处有一开挖单元体(m0,n0,l′)，体积为dmdndl′。在不排水条件下，当此单元体完全塌落时，其上部土体沿z坐标轴方向的变形

。

(5)

式中：r(l′)为主要影响半径，m,r(l′)=l′/tanβ,tanβ=20/(50-φ)，β为上部地层主要影响角，(°);φ为土体内摩擦角，(°)。

在顶管顶进的过程中，管道周围土体受扰动，管土之间会形成环空间隙，从而导致四周土体向管节移动。如图2所示，传统的收敛模型认为地层损失引起的土体移动为均匀收敛，但Longanathan等[6]提出不均匀收敛模型更接近实际。

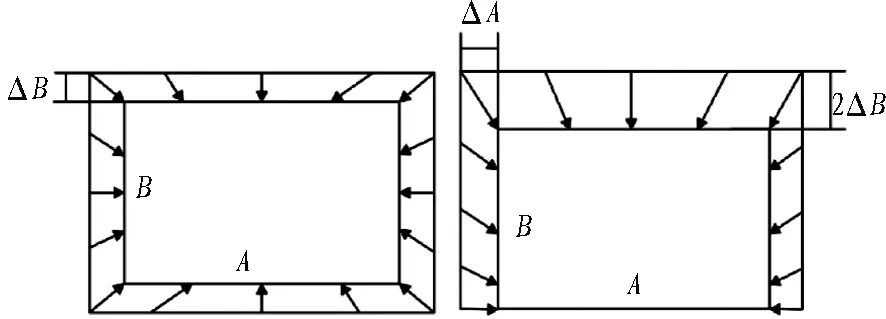
(a) 均匀收敛 (b)不均匀收敛

图2 顶管开挖面收敛模型示意图

Fig. 2 Sketch of convergence model of pipe jacking excavation

face

根据图2(b)模型及前述随机介质公式，可得由于地层损失导致地表任意一点变形的计算公式：

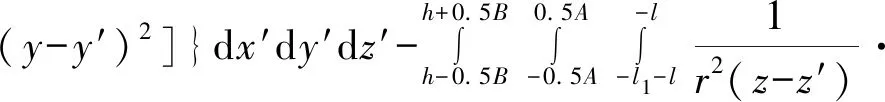
(6)

1.4 注浆引起地表土体竖向位移计算

注浆工艺是矩形顶管施工中优化管土受力的一种重要方式。施工过程中同步注浆且注浆压力大于地层压力，泥浆注入并填充管土间隙，在地层与管节间形成泥浆套。泥浆套主要起到支撑与润滑减阻的作用，并对管土产生附加注浆压力， 从而对土体变形产生影响。

(7)

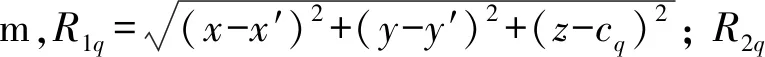
同理，可修改各方向积分区域，依次求出矩形顶管管土之间注浆土压力引起的土体竖直方向位移。

由式(7)可知，地层竖向位移与附加注浆压力呈正相关，但实际过程中由于地层条件、施工条件的改变以及不确定的人为因素，附加注浆压力具有很大的不确定性[19]。针对此情况，可认为注浆填充引起的地层竖向变形是地层损失的逆过程，用随机介质理论进行探讨。假设施工中注浆及时且泥浆渗透不会引起地表土体变形，将土体视为随机介质，则地层因注浆引起的地表抬升为若干个泥浆单元体引起地表抬升的总和。泥浆套在地层中受土压力与附加注浆压力影响，其变形模式如图3所示： 泥浆套受注浆压力作用后产生各向同性径向膨胀变形，变形系数相同； 由于地层竖向方向土压力大于侧向土压力，泥浆套竖向方向收缩、水平方向往外扩张，变形系数相同。

图3 泥浆套变形模式

设单位长度土体膨胀体积为ΔV，Vi为顶进单位长度注浆量，λ为泥浆填充率，其值受泥浆性质、地层性质、施工情况等影响，由于顶进过程中土体塌落至管土间隙，故实际工程中泥浆填充率λ一般取80%～95%[16]即可对周围土体产生支撑作用。令ΔV=(1-λ)Vi，根据其值反算出ΔA′和ΔB′。根据随机介质理论，地表变形为：

(8)

2 工程实例分析

2.1 工程概况

苏州市城北路综合管廊矩形顶管项目，采用组合式刀盘土压平衡式矩形顶管进行掘进施工，断面尺寸为5.5 m×9.1 m，壁厚650 mm，内径为4.2 m×7.8 m，属于大断面矩形顶管工程。顶管结构全部采用预制矩形钢筋混凝土管节，接口采用“F”型承插口。顶进长度为233.6 m，顶管施工段平均覆土厚度为9 m。管节断面如图4所示。

图4 顶管管节断面图

地表沉降监测点采用钻孔技术埋设在路基层中，并通过水准仪进行监测。全线总共设置3个监测断面： CJ1断面、CJ2断面和CJ3断面。其中，CJ1断面距始发井洞门69.37 m，断面上设置23个监测点(如图5所示)，测点范围是CJ1-17～CJ1+17，其中CJ1表示第1个断面，+17表示测点在顶管轴线北侧17 m，-17表示测点在轴线南侧17 m，-0则表示轴线上的点。本文主要对CJ1断面监测数据进行分析。

顶管施工穿越地层从上至下依次为： 素填土、黏土、粉质黏土夹粉土、粉砂夹粉土、粉砂。地层分布情况如图6所示，各土层物理力学参数如表1所示。

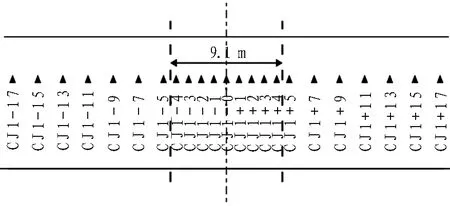
图5 CJ1断面监测点布置图

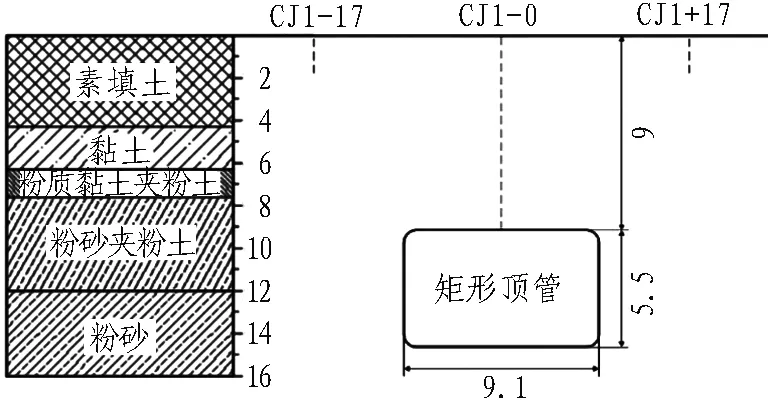
图6 顶管施工穿越地层分布(单位： m)

表1 地层物理力学性质参数

2.2 计算过程

据前所述，矩形顶管施工过程中导致土体变形的主要影响因素为正面附加推力、顶管与土体间摩擦力、管节与土体摩擦力、地层损失以及注浆。假定这些因素之间独立作用，则土体的变形可看作是它们的叠加。

地表土体任意一点竖向变形

wsum=wp+w2+ws+wq

。

(9)

地层参数选取时参考表1，土体物理力学参数取加权平均值。管节参数根据实际工程来取值，计算时为便于考虑，管节断面按矩形考虑。施工参数方面，正面附加应力按式(10)—(12)计算；摩阻力由管节上的正压力(土压力计示数，取均值)与摩擦因数相乘，管节与土体摩擦因数取0.25，机头与土体摩擦因数取0.6；地层收敛模型中，ΔA=ΔB，根据断面收缩体积与地层损失相等可求其结果；注浆模型中，注浆压力通过现场实测取平均值，相关几何参数通过ΔV反算。

P=F1-AB·p0

；

(10)

p=P/(AB)

；

(11)

F1=AB[γ(H+2/3B)tan2(45°+φ/2)+2ctan(45°+φ/2)]。

(12)

式(10)—(12)中：P为迎面阻力，kN；p0为静止土压力，kPa;p为正面附加应力，kPa;F1为设计土舱压力，kN;H为上覆土高度，m。

所有参数最终取值见表2—5。

表2 地层参数计算表

表4 施工参数计算表 Ⅰ

表5 施工参数计算表 Ⅱ

对于上述多重积分函数，可利用Matlab进行数值计算，积分方法采用Guass-Legendre求和公式。

2.3 地表土体竖向变形

2.3.1 理论计算值与实测值比较

选取顶进里程分别为60.34、70.23、80.42、90.11 m时的相关顶进参数，计算出CJ1监测断面的理论沉降曲线，并与实际进行对比，如图7—10所示。由图7可知，顶管顶进60.34 m即工作面抵达监测断面前9.03 m时，地表沉降计算值与实测值整体趋势一致，轴线右侧的地表沉降计算值与实测值拟合度较高，轴线左侧的地表沉降计算值与实测值偏差较大，最大偏差约为4 mm。由图8可知，顶管顶进70.23 m即工作面通过监测断面后0.86 m时，地表沉降计算值整体大于实测值，但两者趋势相同，最大偏差为3.9 mm。由图9可知，顶管顶进80.42 m即工作面通过监测断面后11.05 m时，地表沉降计算值与实测值变化趋势相同，最大偏差5 mm，计算值整体大于实测值。由图10可知，顶进90.11 m即工作面通过监测断面后20.74 m时，地表沉降槽的计算值与实测值变化趋势大体一致，最大偏差4.7 mm，计算值整体大于实测值。总体来说，地表沉降的理论计算值略大于实际值，但沉降槽的整体形式一致、数值相近，最大沉降点的计算值与实测值较为接近。

根据前述结论，轴线正上方的监测点预测结果较为准确。为进一步分析顶管顶进过程中引起的正上方地表变形曲线，将实测值与计算值对比如图11所示。对比发现，理论计算值变化趋势与实测值大体一致。顶管开挖面距离监测面20 m内，理论值与实测值相差较大，可能是实际施工时土体超挖所致；在监测面前后10 m范围内，轴线测点计算值与实测值非常接近； 在顶管通过监测面15 m后，实测值波动较大，主要是人为增加注浆量以有效控制地表沉降，而理论计算时假定注浆量不变，故产生较大误差。

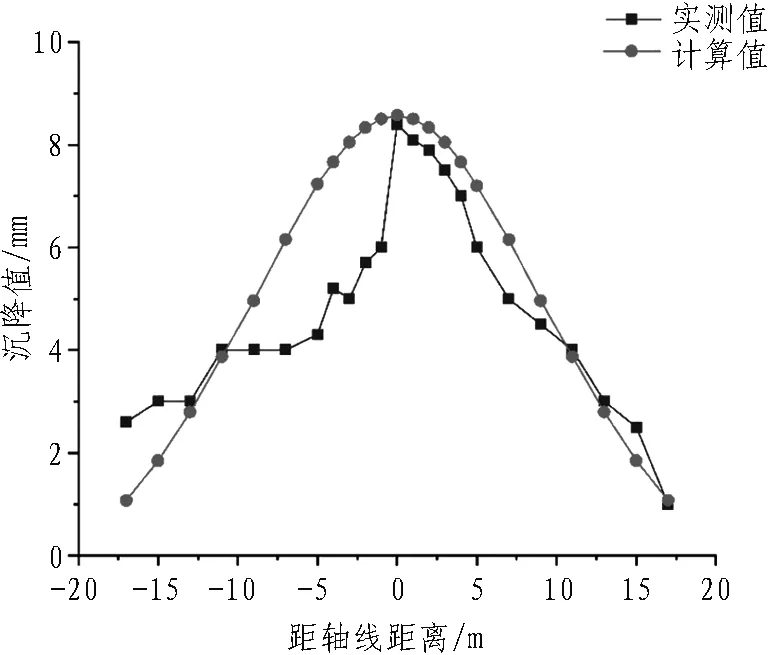
图7 工作面抵达监测断面前9.03 m时沉降槽对比

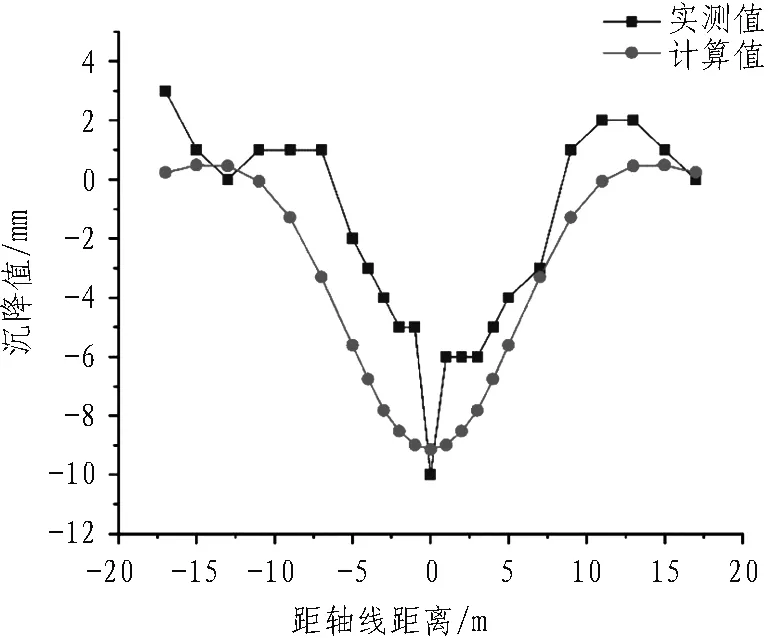
图8 工作面通过监测断面后0.86 m时沉降槽对比

图9 工作面通过监测断面后11.05 m时沉降槽对比

图10 工作面通过监测断面后20.74 m时沉降槽对比

对比图7—10可知： 由于CJ1断面距始发井洞门69.37 m，则顶管顶进60.34 m时还未顶进至CJ1断面，可知大断面矩形顶管正常顶进时，工作面前方土体会有隆起，后方土体沉降；整个顶进过程中，理论与实测竖向位移最大位置为顶管轴线下方左右，且离轴线越远其变形越小，沉降槽随着顶管顶进逐渐变大；理论与实测CJ1断面最终沉降量均为20 mm左右。

图11 轴线正上方地表变形实测值与计算值对比

顶管施工中地表土体竖向变形的理论计算值虽然存在一定偏差，但整体变化趋势与实测值相似；而且，顶管轴线正上方测点预测值与实际值比较相近。因此，本文理论公式较为可靠，可用在类似地层中的地表沉降预测。

2.3.2 探究不同因素对地表竖向变形影响

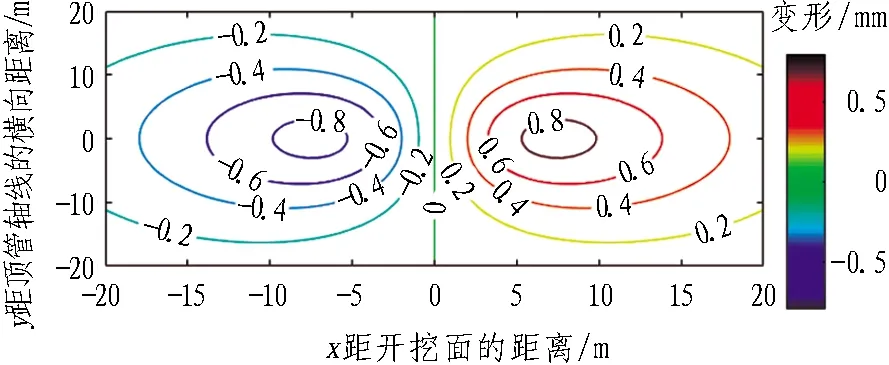
利用Matlab中的ezsurf函数和contour函数做出三维曲线图和等值线图，计算顶管顶进20 m时，各个因素对地表变形产生的影响，如图12—16所示。

由图12可知，附加推力引起地表变形的绝对值关于开挖面对称分布，前方土体表现为隆起，后方沉降。最大隆起为0.8 mm，发生在距离开挖面前方约8.5 m处；最大沉降为0.8 mm，发生在开挖面后方约8.5 m处；开挖面处的地表不受附加推力的影响。

(a)

(b)

surface

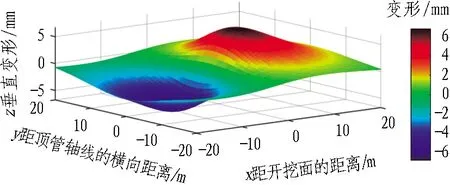
由图13可知，顶管机头摩阻力引起地表变形的绝对值关于x=-3对称，前方土体表现为隆起，后方土体沉降。最大隆起为6.5 mm，发生在距离开挖面前方约5 m处；最大沉降为6.5 mm，发生在开挖面后方约11 m处。

(a)

(b)

由图14可知，管节摩阻力对开挖面后约13 m处地表土体不产生影响，该处前方(x>-13 m)土体表现为隆起，最大隆起约为5 mm，发生在开挖面后3 m处； 该处后方(x<-13 m)土体表现为沉降，最大沉降约为5 mm，发生在开挖面后20 m处。

(a)

(b)

由图15可知，地层损失对开挖面之前的土体扰动很小，对开挖面之后的土体产生的沉降较大，最大约为13 mm，发生在开挖面后14 m处。

(a)

(b)

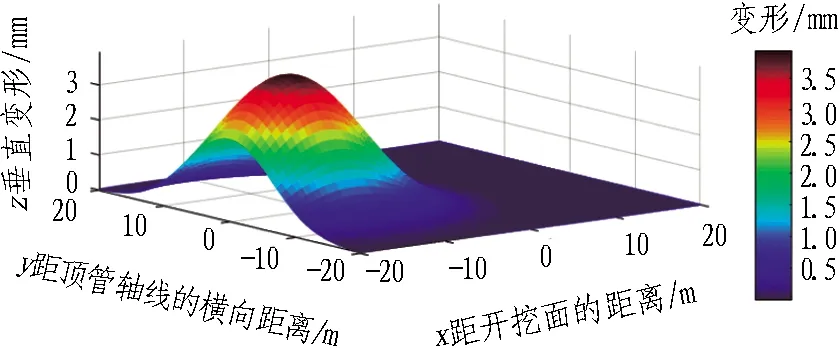
由图16可知，注浆对土体扰动的影响与地层损失对土体的扰动类似。开挖面前方的土体受影响较小，后方土体表现为隆起，最大隆起约为4 mm，发生在开挖面后12 m处。

(a)

(b)

综上所述，矩形顶管正面附加推力对地表竖向变形影响较小；地层损失及注浆对地表竖向变形影响较大，且地层损失引起的土体沉降与注浆引起的土体隆起主要在开挖面之后；机头与管节对土体竖向变形影响规律相似，因其相对位置不同则变形对称线相较于开挖面位置也不同。从计算结果及等值线图看，这几种因素引起的地层竖向变形影响区域为开挖面前后30 m左右，但基于不排水压缩的各向同性线弹性半无限体的土体假定，在顶管实际施工后，由土体固结及泥浆套的变化等因素引发的地层竖向变形与理论计算值不同，但其变形规律相似。

3 结论与建议

本文基于力学理论、实测数据与数值计算等分析方法，对多因素下施工引起的地层竖向变形进行研究，主要结论如下。

1)利用Mindlin基本解及随机介质法，探究矩形顶管施工引起地层变形模式，推导各因素引起的地层竖向变形公式，将其叠加得出地层竖向变形解析式。

2)对比理论值与实测值发现，轴线正上方的监测点理论值与实测值十分相似，开挖面前方土体隆起，后方土体沉降，竖向位移最大位置为顶管轴线下方左右，且离轴线越远其变形越小，沉降槽随着顶管顶进逐渐变大。

3)结合Matlab函数，建立大断面矩形顶管顶进20 m时地层竖向变形曲线图，发现地层损失对地层沉降的影响程度最大，顶管机头与周围土体的摩阻力影响次之，注浆会对地层产生一定抬升效果。由此可以推出大断面矩形顶管顶进时地层竖向变形的一般性规律。

4)施工过程中，应尽量保持开挖面稳定，控制顶管超挖或欠挖程度；提升注浆工艺，控制注浆量、注浆压力及泥浆材料，后期进行二次注浆与浆液置换；对流塑性较差的土体可注入土体改良液。

本文研究设立较多假定，对计算模型作了较多简化，且仅考虑各因素独立共同作用对地层竖向变形的影响，未考虑时间效应及管节圆角部分等因素的影响。另外，注浆对地层扰动的力学效应及体积效应，以及大断面矩形顶管施工时地层水平位移需作更深入的研究。