乘积流形的超曲面上双调和算子的特征值估计

邓严林，侯兰宝，严政

(1. 荆楚理工学院数理学院, 湖北 荆门 448000; 2. 长江大学信息与数学学院, 湖北 荆州 434023)

0 引言及主要定理

设(M,g)是n维欧氏空间n的m维等度浸入闭子流形时, Reilly在文献[1]中给出了M上Laplace算子Δ的第一非零特征值λ1(M)的一个上界估计:

(1)

这里|M|是(M,g)的体积, dvg是(M,g)的黎曼体积元, 而H是(M,g)在n维欧氏空间n的平均曲率向量. 通常, 不等式(1)被称为Reilly不等式. Reilly不等式被推广到不同的流形和算子, 参见文献[2-6]. 最近，Xiong[7]给出了乘积空间(×N,dt2⊕h)的闭超曲面上Laplace算子Δ的第一非零特征值的Reilly型估计, 这里(N,h)是一个完备黎曼流形,h是其黎曼度量. 而Roth[8]则将结果推广到散度型算子、Paneitz型算子等， 关于Paneitz型算子的特征值等周估计结果, 参见文献[9].

在本文中, 我们考虑下述双调和算子特征值问题：

Δ2u-τΔu=Λu, inM

(2)

这里τ是任意正常数. 在物理上, 上述方程是用来刻画圆盘振动问题的, 而τ是与圆盘横向张力相关的常数. 我们知道上述问题有离散的谱：

0<Λ1<Λ2≤…≤Λk≤…,

这里的每一个特征值按照其重数排列. 在文献[10]中, Payne给出了问题(1)式的第一非零特征值的等周估计, 而杜和吴[11]研究了带权情形的特征值估计. 本文中, 我们则得到下述结论.

定理1设(N,h)是一个n维完备黎曼流形, (M,g)是等度浸入到黎曼乘积(×N,dt2⊕h)的一个定向闭超曲面, 且M是平均凸的, 即平均曲率|H|>0. 则对特征值问题(2)式的第一非零特征值Λ1, 可得：

Λ1≤n|H|+(M)κ+(M)(n|H|+(M)κ+(M)+τ)

(3)

这里|H|+和κ+分别表示M上平均曲率和主曲率的最大值,τ>0 为常数.

本文中的第二部分，我们研究buckling问题. 事实上, 我们得到：

定理2在定理1的条件, 设Γ1是buckling问题Δ2u=-ΓΔu的第一非零特征值, 则可得

Γ1≤n|H|+(M)κ+(M)

(4)

注记3在上述定理中, 令N=n, 则乘积流形为n+1=×n,当M=Sn(r)⊂n+1, 可以得到

(5)

此时, 定理1和定理2中等式成立.

1 主要定理的证明

在本节中, 我们将给出第一节中主要结果的证明.

定理 1的证明由极大极小原理可得

要给出特征值的估计, 一个重要的工作是选取合适的测试函数. 设t是乘积流形R×N上R的坐标函数, 既然M沿着t的方向是平移不变的, 则我们可以假设

另一方面, 既然M是平均凸的, 则t在M上不会恒为0. 因而, 可以选取t为测试函数, 可以得到

(6)

直接计算可以得到

Δt=div(t)=〈ei(t),ei〉=

-n|H|u,

(7)

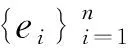
(8)

另一方面,

(9)

在M上对等式uΔt=-n|H|u2和tΔt=-n|H|ut两边积分, 由(7)式和(9)式可得

(10)

(11)

这里h表示M的第二基本形式.

进一步由Cauchy-Schwarz不等式可得

因此, 综合(11)、(12)式可得

n|H|+(M)κ+(M)

(12)

将(12)式代入(8)式可得

Λ1≤n|H|+(M)κ+(M)(n|H|+(M)κ+(M)+τ).

至此, 定理得证.

定理2的证明通过与定理1证明中类似的讨论, 选择t为测试函数, 则由极大极小原理可得

(13)

另一方面, 由(12)式可知

(14)

因此可得

Γ1≤n|H|+(M)κ+(M)

(15)

定理2得证.