基于四元数傅里叶变换的Hartley变换的不确定性原理
王岚,付应雄
(湖北大学数学与统计学学院, 湖北 武汉 430062)
Hartley变换是1942年美国学者Hartley提出的一种把实值函数转换为实值函数的积分变换, 它的正变换与反变换的计算是完全对称的[1].文献[2]中Bracewell指出Hartley变换比傅里叶变换快2至4倍,在计算过程中可以极大提高运算速度和效率.近年来,Hartley变换引起了广大学者的关注,并且在光学、地球物理学与密码学等方面取得了大量的研究成果[3-7].Hartley变换与傅里叶变换同属于正弦型的正交变换,两者之间存在着相互转化的关系[8].四元数傅里叶变换是经典傅里叶变换在高维空间上的推广,它可以将一个二维信号转换成四元数值的频域信号,近些年来成为信号处理的有力工具[9-14].
不确定性原理最初是由德国物理学家海森伯格于1927年提出[15].该原理指出一个信号不可能在时域及频域同时有限,也就是信号的时域和频域的分辨率不可能同时取得确定的值.因此,利用海森伯格不确定原理可以很好地分析信号在时域、频域分辨率的大小关系.目前,经典傅里叶变换及四元数傅里叶变换的不确定性原理已经得到解决[15-17].然而,Hartley变换的不确定性原理却少见相关结论.本研究建立四元数傅里叶变换与Hartley变换之间的关系,进而给出了Hartley变换的不确定性原理.
1 预备知识
1.1 Hartley变换对一维函数f(x)∈L2(R),其Hartley变换及其逆变换分别定义为
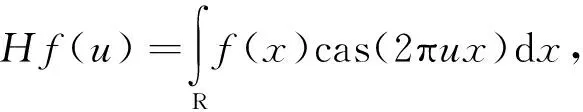

其中cas(2πux)=cos(2πux)+sin(2πux).
对于二维Hartley变换的定义,存在两种不同的形式,根据Bracewell的建议[18],本文中采用标准形式的二维Hartley变换.对二维函数f(x1,x2)∈L2(R2;R),其Hartley变换及其逆变换分别定义为
(1)
其中
cas[2π(u1x1+u2x2)]=cos2π(u1x1+u2x2)+sin2π(u1x1+u2x2),
x=(x1,x2),d2x=dx1dx2,u=(u1,u2),d2u=du1du2.
可以看出,Hartley变换及其逆变换具有完全相同的形式,构成了严格对称的变换,并且Hartley变换在实数域空间中进行.此外,Hartley变换具有傅里叶变换的大部分特征,其性质也与傅里叶变换相似.它的一些性质,如线性性、时间展缩性,与傅里叶变换是相同的,其他的一些性质也很相似.由于Hartley变换是一种把实值函数转换为实值函数的积分变换,所以实数性是Hartley变换最为显著的优点[19].并且Hartley变换满足Parseval定理,即
(2)
可以将(1)式表示为
把Hf(u)写作奇部eo(u),oe(u)和偶部ee(u),oo(u)相加减,则可得:
Hf(u)=ee(u)-oo(u)+oe(u)+eo(u)
(3)
其中
(4)
(5)
(6)
(7)
1.2 四元数四元数[20]于1843年由W.R.Hamilton提出,并以H表示,是一种将复数推广到四维空间的代数
H={q=q0+iq1+jq2+kq3|q0,q1,q2,q3∈R},
其中i,j,k满足
i2=j2=k2,ij=-ji=k,jk=-kj=i,ki=-ik=j.
由于四元数具有非交换性,所以不能直接将复数域上的各种结果推广到四元数. 四元数q可以表示成标量q0(实部)和矢量q(通常也叫纯四元数)和的形式
q=q0+q=q0+iq1+jq2+kq3
(8)
其中标量部分也表示为Sc(q)=q0.特别地,当q2,q3=0时,(8)式表示的四元数是复数,这 时q=q0+iq1∈C.当q1,q2,q3=0时,(8)式表示的四元数是实数,这时q=q0∈R.故四元数是实数和复数的扩充.
四元数q的共轴为q=q0-q=q0-iq1-jq2-kq3.q的模为

对任意的四元数q1,q2,有如下不等式成立
|q1+q2|<|q1|+|q2|
(9)
进而有
(10)
四元数值的函数f:R2→H可以表示为
f(x)=f0(x)+if1(x)+jf2(x)+kf3(x),f0,f1,f2,f3∈R,x=(x1,x2)∈R2.
定义线性赋范空间
L2(R2;H)={f:R2→H,‖f‖2<∞},
其中函数f的范数定义为
1.3 四元数傅里叶变换结合经典的傅立叶变换,学者们提出了四元数傅立叶变换[21-22].四元数乘法的非交换性导致四元数傅里叶变换具有3种不同的定义方式,即右边四元数傅里叶变换、双边四元数傅里叶变换以及左边四元数傅里叶变换.本文中仅涉及到右边四元数傅里叶变换,下面给出右边四元数傅里叶变换的定义.
对二维函数f(x1,x2)∈L2(R2;H),其四元数傅里叶变换及其逆变换分别定义为
(11)
文献[16]中给出了四元数傅里叶变换的一些性质,下面给出四元数傅里叶变换关于变量xk的偏导性,
引理1当i=1,2时,对于f(x)∈L2(R2;H),有如下等式成立
经典的Hartley变换具有实数性,故下文中取函数f(x)∈L2(R2;R)∈L2(R2;H).
引理2Hartley变换如(1)式所定义四元数傅里叶变换如(11)式所定义则对任意的f(x)∈L2(R2;R),四元数傅里叶变换Fqf与Hartley变换Hf之间存在如下关系
(12)
引理2的证明利用Euler公式,我们可以重写(11)式如下:
则四元数傅里叶变换Fqf可写作奇部eo(u)、oe(u)和偶部ee(u)、oo(u)相加减
Fqf(u1,u2)=ee(u)-ioe(u)-jeo(u)+koo(u)
(13)
其中,奇部eo(u)、oe(u)如(5)、(6)式所定义,偶部ee(u)、oo(u)如(4)、(7)式所定义,
相应地有
Fqf(-u1,-u2)=ee(u)+ioe(u)+jeo(u)+koo(u)
(14)
Fqf(-u1,u2)=ee(u)+ioe(u)-jeo(u)-koo(u)
(15)
Fqf(u1,-u2)=ee(u)-ioe(u)+jeo(u)-koo(u)
(16)
结合(13)~(16)式可得
Fqf(u1,u2)+Fqf(-u1,u2)+Fqf(-u1,-u2)+Fqf(u1,-u2)=4ee(u),
Fqf(u1,u2)-Fqf(-u1,u2)+Fqf(-u1,-u2)-Fqf(u1,-u2)=4koo(u),
Fqf(u1,u2)+Fqf(u1,-u2)-Fqf(-u1,-u2)-Fqf(-u1,u2)=-4ioe(u),
Fqf(u1,u2)-Fqf(-u1,-u2)+Fqf(-u1,u2)-Fqf(u1,-u2)=-4jeo(u),
从而,由(3)式可知结论成立.
2 不确定性原理
不确定性原理是信号处理领域中重要的原理之一[15],它说明任何信号在时间域与频率域不可能同时是有限支撑的,也就是说较窄时间波形产生较宽频谱,而较宽的时间波形产生较窄的频谱, 时间波形的宽度和频谱宽度不可能同时任意小.下面首先给出函数f(x)在时间域和频率域上的支撑的定义.
定义1当i=1,2时,对任意的变换T,f(x),xif(x)∈L2(R2;R),Tf(u),uiTf(u)∈L2(R2;R),f(x)在时间域上的支撑Δxi定义为
其中
同样地,我们定义f(x)在频率域上的支撑为
其中
下面给出关于实函数f(x),g(u)的施瓦茨不等式:
引理3[23]设f(x),g(u)在L2(R2;R)上可积,则
利用上述引理1~3,进一步讨论Hartley变换的不确定性原理.
定理1若定义1中变换T取如(1)式所定义的Hartley变换Hf,且满足‖f‖2=1时,有如下不等式关系成立
(17)
进一步有
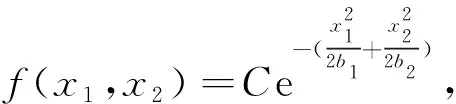
定理1的证明(12)式可整理为
则
同理可得到Hf(-u1,u),Hf(u1,-u2),且由(12)式计算可得
|Hf(u1,u2)|=|Hf(-u1,-u2)|=|Hf(-u1,u2)|=|Hf(u1,-u2)|
(18)
利用引理2,经计算可得
由(10)、(18)式及Hf的实数性,经计算可得
|Hf(u1,u2)|2+|Hf(-u1,-u2)|2+|Hf(-u1,u2)|2+|Hf(u1,-u2)|2=
4|Hf(u1,u2)|2
从而,利用引理1、引理3以及(2)式,有如下不等式成立
其中l∈{1,2},l≠i.(17)式得到证明.
进而可得