几何直观在分数教学中的应用

江苏省常熟市东南实验小学 章如军

在小学数学学习过程中，分数是相对抽象且比较难以理解的对象，苏教版分别在三上、三下、五下、六上四册教材中安排了分数知识的教学，这些知识块都可以借助几何直观，通过形象的方式描述出来，变抽象为具体，帮助学生更好地理解和掌握。

一、借助几何直观理解分数概念

在概念形成的过程中，具体的操作活动是学生认识概念的起点，这种具体的直观形象会影响学生头脑中概念意象的形成质量。有了操作实践为保证，丰富、拓展了认知表象，学生就能够正确理解意义。分数概念中，单位“1”的认识一直是教学的难点，在三下“认识分数”中，主要教学的是将几个物体看成整体进行平均分，教材提供了4 个小猴分桃子的图片，引导教师采用几何直观帮助学生理解。教学过程如下：

1.认识一盘桃的。

（1）课件出示：猴妈妈为小猴们准备了一盘桃子（4 只）。出示题目中的问题：把一盘桃子平均分给4 只小猴，每只小猴分得这盘桃的几分之几？

（3）我们来回想一下，我们是把这盘桃怎么去分的？其中的一份怎么用分数来表示？谁来完整地说说？课件出示：把一盘桃平均分成（）份，每份是这盘桃的（）。学生相互交流。

（4）那么这一份（指着另一份）是这盘桃的几分之几呢？学生交流。

2.深入认识。

（1）猴妈妈又拿来了一串香蕉，一共有几根？（8 根）还是要平均分给4 只小猴，应该怎样分？每份是几分之几呢？

（2）学生拿出圆形纸片分一分，并和同桌说一说。学生汇报，课件演示。

（3）比较：

二、借助几何直观沟通分数计算算理

教学分数计算的时候，很多老师往往重算法轻算理，这种做法短时效应很突出，但在后期两级运算后，学生缺少对算理理解的弊端就越发显现，将极大地影响学生的计算能力。分数的计算和整数、小数的计算方法有着显著的差别，但教师可以借助几何直观来帮助学生理解算理，体会算法上的不同。

如在六上“分数除法”中教学整数除以分数时，出示例题：

整数除以分数的算理是个非常抽象的内容，依靠其他方式很难说清，借助几何直观能够为学生的思维架构桥梁。这个例题的教学借助几何直观可以分以下几个层次展开：

4.抽象概括。观察等式两边两个相等的式子，你有什么发现？

这个教学过程是“抽象—直观—抽象”的过程，借助直观的图形，将抽象的问题明了化，在解决问题之后，通过对比提炼出计算方法。列出算式，直观感知结果，建构直观模型，提炼概括，这个过程是分数四则运算学习的一般过程。几何直观作为抽象的终点，又是抽象的起点，图形帮助我们找到了正确的结果，更为主要的是，根据图形，使学生理解分数与整数相乘的算理，沟通其与算法的联系。

三、借助几何直观厘清分数数量关系

在学习数学的过程中，对数量关系的理解一直是学生学习的难点。进入分数学习后，因为分数的抽象性，更增加了这方面的难度，所以在教学中更应借助几何直观，用图形表达题意，理解数量关系。如六年级上册这道例题：

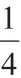
2.看图分析，确定解题思路。

3.学生列式，完成解答。

这道习题复杂在有“原来、下车、上车、现在、多了”这5 个量，量间相互关联，加上又有两个分数，就给解题带来了很大的困难，学生在读题后往往无从下手，难以厘清数量关系，但若能尝试画线段图，就可以使它们之间的关系一目了然。

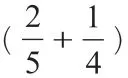
四、借助几何直观探索分数规律

将抽象的分数用直观的图形表示出来，这种数形结合的方法能够帮助学生在解决问题时另辟新径，发现内中规律。如在六年级下册“解决问题的策略”里有这样一题：

学生第一次遇到这个算式的时候通常都是通分计算，题目里的数学规律不易被发现。但借助直观的图形，就可以将数字间的联系呈现出来，为学生接下去的规律探索提供可能。教学可以这样展开：

1.计算解决，引发思考。出示题目，学生计算后交流，估计都是通分的方法。提出问题：还有没有别的方法？引导学生发现算式中数字间的联系。

2.引导画图，感受规律。出示长方形，引导学生将这个算式在图上表示出来，学生在画图和交流中体验转化策略，感受规律。

3.探究延伸，内化规律。学生通过画图找到简便计算的方法后，教师继续提出问题：这个算式如果还要往后写，接下去的加数会是多少？和呢？你有怎样的发现？通过追问，让学生主动回顾题目特点，进一步掌握和运用规律。

用图形来表示数，数字间原先内隐的关系直观化了，几何直观帮助我们从另一个角度来研究分数，进而发现了藏在里面的规律。

用几何直观描述问题，用几何直观讨论问题，能够帮助学生理解和掌握分数知识，发展学生思维内涵，提高基本的数学素养。