智能车辆换道控制研究
胡远志,肖 航,刘 西,刘小勇
(重庆理工大学 汽车零部件先进制造技术教育部重点实验室,重庆 400054)
当前,频发的汽车交通事故已成为严重危害公共安全的一大社会问题。据欧盟数据统计,由车道变换引起的事故占汽车总事故的4%~10%,并导致了10%的道路堵塞问题[1]。智能车辆的自主换道功能可有效避免因驾驶员换道判断失误和操作不当等因素造成的交通事故的发生,缓解交通拥堵状况,提升通行效率。要实现智能汽车的自主换道,主要需考虑以下因素:①换道意图的确定及换道决策;②规划安全、舒适的换道轨迹;③设计合理的路径跟踪控制算法来保证智能汽车对规划路径的准确跟随。
目前换道行为决策模型主要有MITSIM模型、CORSIM模型和SITTRAS模型[2-4]。MITSIM模型以忍耐因子、速度差因子作为换道的依据;CORSIM模型通过分析不可忍受的速度极限值来决定换道动机的产生;SITTRAS模型基于本车和目标车道前/后车的加速度是否超出驾驶员可接受程度作为换道意图产生依据。
常用的路径规划有基于圆弧[5]、五次多项式[6-8]、三角函数[9-11]、梯形加速度轨迹[12]、B样条曲线、β样条曲线等的规划方法。文献[8]在目标函数和多种约束的情况下基于五次多项式设计了直线道路和弯道的换道轨迹;文献[10]基于恒速偏移正弦曲线来建立换道轨迹规划的模型;文献[12]基于正梯形和负梯形横向加速度方法计算车道变换轨迹,基于多目标优化实现了换道操作。
在轨迹跟随方面常用的控制算法有PID控制算法、滑模控制算法、智能控制算法、模糊逻辑控制算法和自适应控制算法等。上述方法的控制参数对所处环境的依赖较高且难以处理车辆运行过程中的运动学约束与动力学约束。
本研究以安全距离和速度的不满累计度作为换道意图的产生依据,基于最小换道安全距离来实现车辆的换道决策,利用五次多项式拟合确定车辆换道轨迹,采用模型预测控制算法实现对规划轨迹的跟踪。
1 换道意图
根据安全距离与速度不满累计度作为换道意图产生依据。假设智能车检测到前方低速车辆,为了避免与前方车辆发生碰撞等事故且追求更好的驾驶空间,其在目标车道存在安全、舒适的驾驶空间的条件下选择自主换道。图1为车辆换道决策控制流程。
1.1 基于速度期望的换道意图
假设主车辆在行驶过程中的期望车速一定,前方车辆缓行。对主车与前方缓行车辆速度差值进行累加得到速度不满累计度。
式中:Z为不满累积度;Vdes为设定的期望车速;V为当前时刻的实际车速;T为采样时间;k为当前时刻。当不满累积度超过设定阈值(Zthr)时,则产生换道意图,即:
1.2 基于车间间距的换道意图
车辆在行驶期间,为了防止与其他车辆发生碰撞,在两车辆之间所保持的足够安全距离(safe spacing,SS)即为跟车安全距离。由于两车以一定的相对速度跟随行驶,两车安全间距与后方车辆车速成线性关系,因此可以推测出跟车安全距离模型为式中:SS表示本车道内两车安全距离;v为后车速度;tb为后车制动延迟时间,一般取1.2~2 s;d0为停车时心理安全距离,一般取3~5 m。
车辆换道空间如图2所示,可知车辆产生换道意图的条件为
当本车道内两车间实际距离小于SS或不满累计度Z(k)大于阈值时产生换道意图。
2 换道可行性分析
当智能车辆产生换道意图后,还需结合实际的道路交通环境来确定能否安全换道。当换道条件都满足时,再执行换道操作。本文引入最小换道临界碰撞安全距离来确定换道的可行性。最小换道临界碰撞安全距离是指避免换道发生碰撞时两车之间必须保持的间距,即最小安全距离(minimum safe spacing,MSS)。
2.1 M 车与L0车的最小安全距离
L0车为行驶在主车辆M前方的车辆。考虑M车换道期间与L0车在临界碰撞位置发生角碰的情况,建立两车位置关系如图3所示。图中M车的车速为vM,L0的车速为vL0。M车在换道初始时刻与L0车的车头间距为S(0),车辆从t=0时刻开始换道,经过tp1到达所示的临界碰撞位置。选取M车、L0车的车头中点作为参考点,推导出主车在换道期间不发生碰撞的条件为[14]:
式中:aM与aL0为本车与前车的加速度;vM与vL0为本车与前车的速度;LL0为L0车的车身长度;wM为自车宽度;R为道路曲率半径。
假设汽车换道过程中车速不发生变化,则可推导出汽车换道时与本车道前车的最小安全距离为
当汽车直线行驶时,认为道路曲率半径无限大,则最小安全换道距离为
2.2 M 车与Ld车的最小安全距离
假设换道期间Ld车维持车道保持的行驶状态,分析两车的位置关系,M车在换道期间不发生碰撞的条件为:
式中:tp2为两车临界碰撞时刻;tc为换道完成时刻。若弯道曲率半径趋于无穷,则可认为是直线换道,其最小安全距离为:
2.3 M 车与Fd车的最小安全距离
假设换道期间Fd车维持保持的行驶状态,分析以两车的位置关系,M车在道路上换道安全距离为:
式中:t∈[tp3,tc],tp3为换道临界碰撞时刻;S(0)为两车初始距离;aM、aFd、vFd分别为M车与Fd车的加速度与速度;LM、wM为M车长度与宽度。
当道路为直线时,可认为道路的曲率半径趋于无穷,则最小安全换道距离模型为
3 轨迹规划与轨迹跟踪
当确定汽车具有换道意图且换道可行后,智能车将进行路径规划及路径跟踪操作。采用五次多项式拟合来实现路径规划,利用模型预测控制算法来实现路径跟踪。
3.1 轨迹规划
多项式计算简单,适应性强,只需知道车辆换道的初始状态和结束状态。与此同时,该函数及多阶导数的曲率连续且光滑,满足换道轨迹的要求。因此本文由多项式曲线来描述车辆的换道轨迹。
调查显示,产生换道意图的主要因素包括前方有慢车行驶、自由换道、转向需要、避障以及前方车道结束,而由于前方存在慢车引起的换道占76%[13]。图6为车辆换道诱因比例示意图。
本文主要研究汽车在城市快速通道及高速公路高速行驶时前方车辆缓行的交通场景,故只考虑本车向左侧变道进入高速车道的情景。
假设多项式换道轨迹的初始状态和结束状态均为已知,对三次、五次、七次多项式进行仿真对比。由图7可知三次多项式轨迹规划曲线较为平缓,但在开始换道与换道终了时刻的横向速度与加速度较大,易造成乘员不适,且到达目标车道所需时间较长;七次多项式轨迹规划容易使汽车在换道过程中产生过大的横向加速度,造成汽车失稳;五次多项式介于三次与七次之间,因此本文选用五次多项式所规划的轨迹作为换道轨迹。
3.1.1 直线换道轨迹规划
汽车规划轨迹如图8所示,其五次多项式换道轨迹的函数为
根据车辆换道开始时的位置和状态,纵向起点为零,初始的横向位移、横向速度和横向加速度均为零,轨迹函数应满足如下约束方程:
由式(13)可得a0=a1=a2=0,经过纵向距离D,车辆换道操作完成。根据车辆换道结束时的位置和状态,其横向位移为W,横向速度和横向加速度均为零,轨迹同样满足以下约束方程:
可以发现,换道轨迹的横向位移yd关于换道纵向位移D、换道时纵向位移xd、车道宽度W的函数为
假设自车的纵向初速度为vx,换道初始时间为0,换道结束时间为tc,yd可表示为:
式中t∈[0,tc]。假定汽车在换道过程中纵向速度不变,即vx(t)=vx,则式(16)可转化为关于时间的函数。
假设换道总时长tc=4 s,取车道宽度为3.75 m,分别以车速72、90、108 km/h进行仿真验证。直线道路轨迹规划仿真结果见图9。
3.1.2 弯道换道轨迹规划
只考虑左换道的情况,图10表示车辆从外车道向内车道换道的轨迹示意图。原点O为车辆初始时刻的质心位置,以O为原点建立如图9所示的大地坐标系。假设弯道内外侧双车道的中心线具有相同的瞬心OR,X轴沿着外车道中心线切向方向,Y轴为指向弯道道路瞬心,C为车辆的质心位置。外车道中心线的曲率半径为R,两车道的间距用W表示。弯道上车辆的横摆角为φ,vx与X轴的夹角以及vy与Y轴的夹角均为α,即为车辆质心绕RO转过的角度。
假设换道开始时刻为0 s,当车辆由外侧车道向内侧车道换道时,经过t时刻后,车辆换道时沿弯道瞬时中心由外侧向内侧的横向位移为yd(t),质心C的瞬时半径可以表示为R-yd(t),α可以表示为
经过几何关系推导,可得车辆在弯道上的换道轨迹为:
在Matlab中进行仿真分析弯道换道轨迹。假设换道初始时刻t=0,车辆初始位置x(0)=0,y(0)=0,换道时间tc=4 s。车速分别为72、90和108 km/h,两车道的间距W为3.75 m,仿真结果如图11所示。
3.2 轨迹跟踪
采用模型预测控制算法来实现轨迹跟踪,利用系统当前的状态和控制量预测未来状态并不断调整系统的控制量。在控制过程中,系统未来的状态是随时变化的,但在控制过程中根据系统的输出实时反馈校正,不断优化追求最优解,使得系统的输出与参考轨迹尽量贴合。
采用3自由度汽车模型作为模型预测控制器的预测模型,利用Carsim中的汽车动力学模型作为被控模型[15]。
汽车在x、y、z方向的受力为:
式中:a、b表示为车辆质心到前、后轴的距离;m表示车辆整备质量;Iz为车辆绕z轴的转动惯量。
轮胎在x和y方向上受到的力与纵向力、侧向力的关系为:
轮胎的纵向力、侧向力由轮胎侧偏角、滑移率、路面摩擦因数和垂向载荷等因素的复杂函数表示为:
式中:α为轮胎侧偏角;s为滑移率;u为路面摩擦因数;Fz为轮胎的垂向载荷。
根据3自由度模型中的速度关系,联立推导出如下关系:
车辆在换道期间的侧偏角及纵向滑移率通常较小,轮胎力不会进入非线性区。与此同时,鉴于其在侧向加速度a≤0.4g的情况下对常规轮胎具有较高的拟合精度,因此可以用线性函数近似描述轮胎的纵向力和侧向力为:
式中:r为车轮半径;w为车轮旋转角速度。本研究假设汽车自带性能良好的ABS系统。
不考虑汽车质心的偏移,前后车轮的垂直方向上的受力为:
通过简化得到前后轮的侧偏角为:
小角度假设下的轮胎纵向力、侧向力为:
将上式代入式(20)可得:
在车辆动力学模型系统中,将前轮转角选取为控制量,即u(t)=[δf],状态量输出量为η(t)=[φ,Y]T。其换道避撞控制系统框图见图14。
4 仿真及结果分析
4.1 控制参数选取及运算实时性
不同的控制参数直接影响控制器的控制效果和计算时间。本文通过对采样时间Ts、预测时域Tp和控制步长Nc的测试选定合适的控制参数。设定测试车速为72 km/h,路面附着系数为0.8。
4.1.1 采样时间Ts
设计控制器A、B和C,其预测时域相同,而采样时间分别选取0.02、0.03、0.05 s,因此预测时域Tp=Np*Ts=0.6 s。为便于分析,设置控制步长与预测步长相等,具体参数见表1。仿真结果如图15所示。
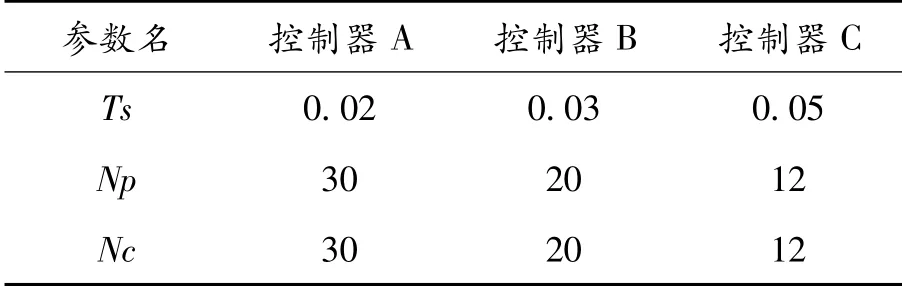
表1 不同采样时间下控制器的控制参数
通过分析A、B、C三个控制器可知,在相同的预测时域内,采样时间Ts越小,线性模型预测控制器的轨迹跟踪情况越好,与参考轨迹的偏差越小。
4.1.2 预测时域Tp
设定控制器D、E、F的预测步长Np分别为10、20、30,预测时域分别为0.3、0.6、0.9 s。设置控制步长与预测步长相等,具体参数见表2,仿真结果如图16所示。
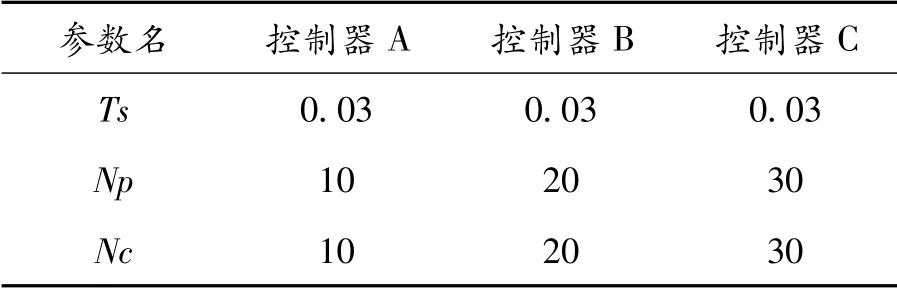
表2 不同预测时域下的控制器控制参数
对比3个不同参数的控制器,在相同的采样周期内,控制器的预测时域越长,车辆跟踪的实际轨迹与参考轨迹的贴合程度越差,运算时间越长。
4.1.3 控制步长Nc
为在不同的控制步长下仿真分析控制器的性能,设计相同预测时域和采样时间下的不同控制器G、H和I。具体参数见表3,其仿真结果如图17所示。
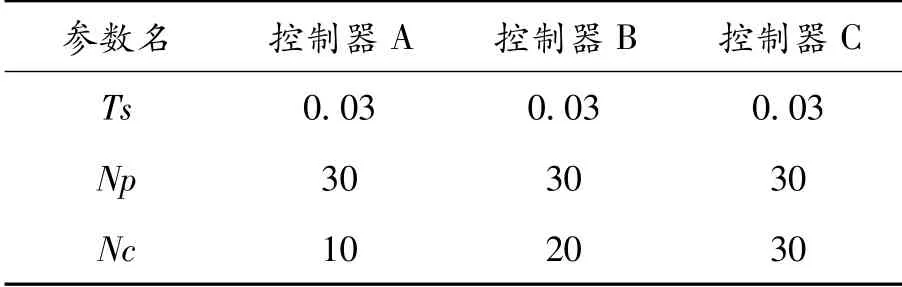
表3 不同控制步长下控制器的控制参数
对比3个不同参数的控制器发现:在相同的预测时域和采样周期内,控制步长越小,车辆跟踪的实际轨迹与参考轨迹的贴合程度越差;控制步长越大,运算时间越长。
由图15~17可知:控制器的运算周期维持在0.01 s左右可以保证汽车控制的实时性。通过对比发现,控制器的采样时间越长,计算时间越短;预测时域过大会造成运算时间长且影响轨迹的跟踪效果,控制步长为预测步长一半左右时控制效果较好。综合考虑各参数的影响,本文选取采样时间Ts=0.03 s,预测时域Tp=0.6 s(Np=20),控制步长Nc=10。
4.2 不同速度不同路面附着条件下的仿真分析
仿真模拟中整车动力学系统采用Carsim仿真平台中的某轿车,整车参数如表4所示。选择车辆在μ=0.4、0.6、0.8的附着条件下仿真验证车速为72、90、108 km/h时的控制算法鲁棒性。

表4 整车参数
4.2.1 路况良好路面(μ=0.8)
由图18可知:汽车在各个车速下均能安全地实现换道操作,虽然在换道结束时存在一定的抖动现象,但汽车实际轨迹与规划换道轨迹的偏移量较小,质心侧偏角、横摆角速度以及前轮转角均在合理范围内。
4.2.2 湿滑路面(μ=0.6)
由图19可知:车辆以不同的速度行驶在湿滑路面时,车辆实际的行驶轨迹与换道参考轨迹基本贴合。但随着车速增大,车辆跟踪的偏差逐渐增大,跟踪路径与期望路径偏差最大为0.42 m。换道过程中质心侧偏角最大值低于4°,车辆横摆角速度处于正常范围内,前轮转角曲线平滑且连续,且车辆前轮转角、最前轮转角与前轮转角增量均在安全范围内。总体来说,车辆以不同车速行驶在湿滑路面时控制系统跟踪效果较好,能满足轨迹跟踪的精度要求。
4.2.3 雪地路面(μ=0.4)
通过图20(a)可知:车辆行驶在湿滑路面时,车辆跟踪的偏差逐渐增大,其跟踪路径与期望路径偏差最大为0.47 m,其最大值质心侧偏角低于2°,车辆横摆角速度也处于可接受范围之内,前轮转角曲线平滑、连续且车辆前轮转角最大值为2.6°,前轮转角增量同样在合理范围内。总体来说,以不同车速行驶在雪地路面时,控制系统跟踪结果良好,能满足轨迹跟踪的精度要求。
由综合仿真实验结果可知:车辆以不同的车速进行轨迹跟踪时,系统的输出量、状态量以及控制输入量、质心侧偏角等都在设定范围内。说明所设计的控制器对不同附着系数路面和车速等因素具有广泛的适应性和很好的鲁棒性,满足实际换道工况。
5 结束语
本文从车辆换道意图、最小安全换道距离、轨迹规划及轨迹跟踪等方面对智能车辆换道控制进行了研究。利用安全距离与速度不满累计度作为换道意图产生依据,根据最小换道安全距离进行换道决策,采用五次多项式拟合来实现换道轨迹的规划,最终采用模型预测控制对规划轨迹进行跟踪。为了获取良好的控制器参数,对控制器参数进行了9种调整,并通过对比实验获得了较好的控制器参数值。最后基于Simulink/Carsim/Prescan分别在道路状况良好路面(μ=0.8)、湿滑路面(μ=0.6)、雪地路面(μ=0.4)对换道控制进行了仿真实验,结果表明在各种路面下汽车均能安全地实现换道操作。

