智能汽车自动紧急避撞系统的安全距离模型及其对比分析

来 飞，黄超群，董红亮

（1.重庆理工大学 汽车零部件先进制造技术教育部重点实验室，重庆 400054；2.重庆工商职业学院 智能制造与汽车学院，重庆 401520）

1 研究现状

随着汽车数量的日益增多，其引发的交通安全问题也越来越突出。自20世纪80年代以来，继汽车防抱死制动系统（anti-lock braking system，ABS）为代表的汽车电子控制系统得到成功应用后，车身电子稳定性程序（electronic stability program，ESP）等主动安全系统得到市场的普遍认可。近年来，以车辆前撞预警系统（forward collision warning，FCW）、车道偏离预警系统（lane departure warning，LDW）、自动紧急制动系统（automatic emergency braking，AEB）为代表的先进驾驶员辅助系统得到快速发展，在减少人员伤亡方面发挥了重要作用。

智能汽车自动紧急制动系统作为汽车主动避撞的一种方式，是在ABS、FCW 基础上演化而来，通过车辆主动制动来防止追尾等碰撞事故的发生。目前市场上已有部分AEB产品问世，国家也出台了相应的标准来对其性能要求进行规范［1］。但在某些工况条件下，面对突然出现的障碍物，通过自动紧急制动系统难以避免碰撞，而此时通过自动转向却能避免，因此自动紧急转向是解决汽车避撞问题的另一有效措施。相比自动紧急制动而言，自动转向系统的研究难度相对较大，其中避撞安全距离模型更是主动避撞系统的核心问题。在紧急情况下，避撞系统的介入时机尤为关键，介入过早会影响驾驶员正常驾驶，介入太晚则会导致无法成功避撞。因此，掌握合适的避撞时机是主动避撞系统的关键，而其首要条件就是提出一种合理的安全距离模型。

目前，智能汽车常见的主动避撞有3种方式：制动避撞、转向避撞和联合制动及转向的综合避撞。盘朝奉等［2］采用自动制动避撞方式，对运动前车进行了不同工况下的仿真分析与实车验证。部分研究者对转向避撞进行了研究，Z.Shiller等［3］采用自行车模型，提出了在转向避撞过程中所需要的最小纵向距离，其位置约束条件为本车与前车障碍物的边界刚好重合；A.Seewald等［4］提出的侧向位移约束条件为本车质心与前车障碍物后端边界在横向位置上保证一定的安全距离；G.Bevan等［5］提出了跟踪预定义参考轨迹的方法来进行避撞。也有部分研究者对制动与转向联合避撞进行了研究。其中，Y.Hattori等［6］提出了一种更加柔和的换道模型，使车辆在换道后时刻的侧向速度为零；R.Isermann等［7］提出的换道约束与文献［4］类似，区别在于前者考虑了障碍车辆的纵向轴线与本车行驶方向成一定夹角；R.Hayashi等［8］提出了由两段圆弧组成的避撞轨迹；V.Fors等［9］提出了一种最优控制算法，其优化准则是车辆初始速度和最终速度的一系列线性组合；GaoYangyan等［10］将避撞过程分成车道变换和车道恢复两个阶段，通过改进的哈密顿算法来进行避撞。

上述研究中绝大部分都使用了安全距离模型，但所提出的安全距离模型大多各不相同，往往都是基于某一特定模型展开研究，未能进行全面客观的定量对比分析和评价，不能较好地指导避撞系统的设计与开发。基于此，本文在建立车辆避撞质点模型和考虑车辆外形尺寸的避撞模型基础上，从运动学角度出发，对主动避撞系统中较常见的安全距离模型进行了仿真计算和定量的对比分析，为主动避撞控制系统的设计提供参考。

2 质点模型

以制动或转向为控制策略的主动避撞基本原理如图1所示，制动避撞以低速情况下使用较多，如图1（a）所示，但当车速较高时，采用转向避撞所需的最小纵向距离更短，因而更为有效。而在转向避撞的控制策略中，有假定车辆换道结束后就保持稳定的，如图1（b）所示，也有假定车辆换道结束后侧向速度不为零的，如图1（c）所示。可以定性地得出：当车速较高时，制动避撞所需的纵向安全距离最大，转向避撞方式1所需的纵向安全距离次之，转向避撞方式2所需的纵向安全距离最小，但此时车辆所需的侧向位移最大。

2.1 模型建立

为定量地分析不同避撞方式所需的最小纵向距离，同时考虑制动与转向相结合的情况，建立起车辆避撞质点模型。不失一般性，以转向避撞方式1为例，车辆避撞质点模型如图2所示。

图2 中，车辆坐标系为xoy，地面坐标系为XOY，汽车在XOY坐标系下的运动方程为：

进一步地，由轮胎物理特性和牛顿第二定律，可得：

式中：m为整车质量；Ψ为车辆航向角；Fx和Fy为车辆坐标系下轮胎作用在车辆质心处分别沿x方向和y方向的合外力；ax、ay分别为车辆的纵向和侧向加速度；ax，max、ay，max分别为车辆的纵向最大加速度和侧向最大加速度；u为路面附着系数；g为重力加速度。

引入状态变量ζ＝［X，Y，vx，vy］，系统输入U＝［Fx，Fy］，则车辆避撞运动的状态方程为

2.2 约束条件

假定车辆避撞前的初始状态为X（0）＝X0，Y（0）＝Y0，vX（0）＝vX0，vY（0）＝vY0，避撞结束时刻t的状态为X（t）＝Xt，Y（t）＝Yt，vX（t）＝vXt，vY（t）＝vYt。设系统初始时刻状态为［0，0，vx，0］，为使得车辆所需的纵向避撞距离最小，则相当于求出系统输入U使得Xt最小。

考虑通过5种不同的操纵方式来完成避撞操作，即制动避撞、转向避撞方式1、转向避撞方式2、制动+转向避撞方式1、制动+转向避撞方式2。则系统输入、约束条件即车辆t时刻状态如表1所示，其中a为车辆换道结束时刻所需侧向距离。

表1 不同避撞方式下的系统输入和约束条件

2.3 仿真分析

针对不同车速下的5种避撞方式，通过Matlab仿真平台分别在高、低两种不同附着路面下进行优化求解，所得出的纵向安全距离计算结果分别如表2、3所示。可以看出：当车辆在高速情况下紧急避撞时，转向避撞方式所需的纵向距离要小于制动避撞；对于转向方式1而言，当车速大于75 km／h时，其避撞所需安全距离要比制动避撞要小，而对于转向方式2而言，在相同的侧向位移即a为3.5 m的约束条件下，当车速大于53 km／h时，避撞所需安全距离比制动避撞要小。同时还可看出，当速度越高、路面附着系数越低，效果越明显。同等条件下，转向方式2所需的纵向距离要小于转向方式1。值得注意的是，在高附着路面上，制动+转向1方式下，打*部分对应的车速为63 km／h，制动+转向2方式下对应的车速为45 km／h；在低附着路面上，制动+转向2方式下对应的车速为28 km／h。

此外，不同制动+转向组合方式避撞下，与对应的纯转向避撞方式相比，其所需的纵向距离有进一步的降低。以车辆在高附着路面上以不同初始车速行驶情况为例，图3表明了通过制动与转向方式1联合避撞时，所需的纵向距离随车辆侧向加速度的变化规律曲线，于是可方便求出每种工况下所对应的最小纵向距离。

表2 高附着路面下的安全距离对比（μ＝0.8）

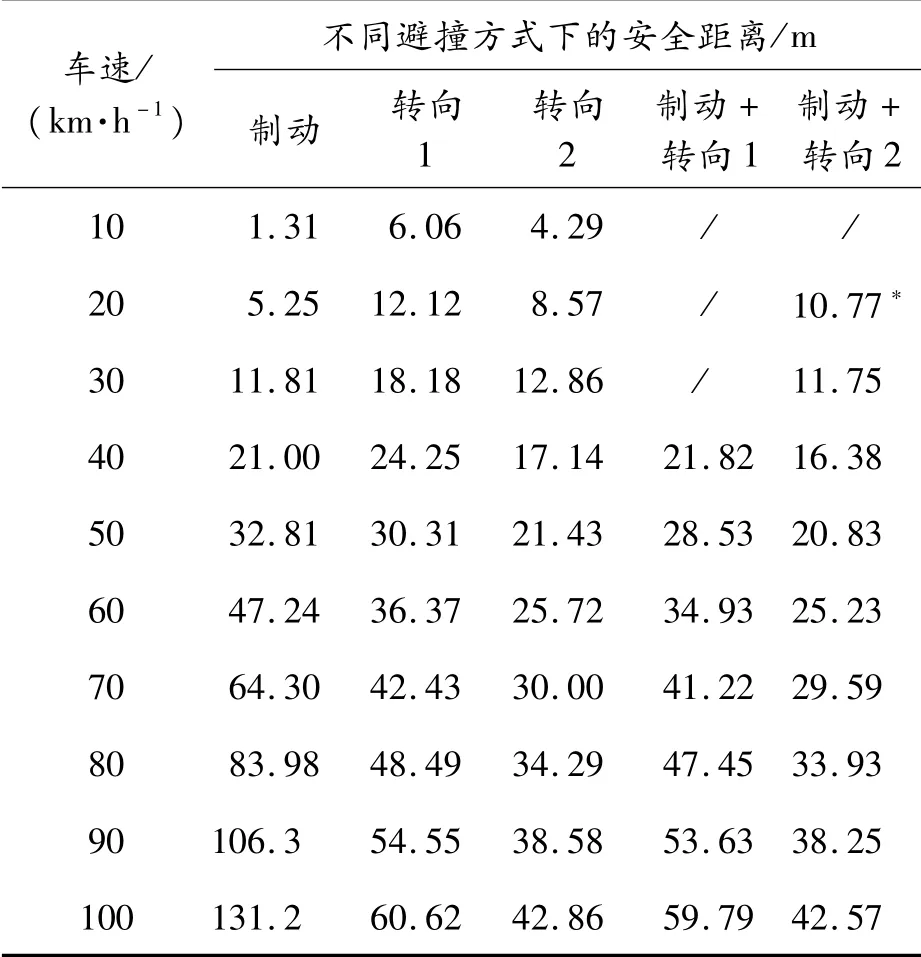
表3 低附着路面下的安全距离对比（μ＝0.3）

可以看出：随着初始车速的逐渐增加，避撞所需最小纵向距离所对应的车辆侧向加速度也随之增加。这也表明，在车速较高的情况下，对于车辆的稳定性提出了更高的要求。此外，通过计算发现：在该种组合避撞条件下，当车辆以70、80、90和100 km／h的初始车速进行避撞时，换道结束时刻车辆对应的纵向速度分别为43.3、58.1、72和83.4 km／h，每种工况下对应的纵向车速大致减小20 km／h。同时，从表2还可得出：在高附着路面上分别以上述初始车速进行避撞时，与纯转向避撞方式1相比，组合避撞下所需的最小纵向距离分别由25.98、29.7、33.41、37.12 m减小为23.8、27.87、31.82、35.72 m，每种工况下大约能降低2 m。

3 五次多项式避撞参考路径规划

通过质点模型对5种不同的避撞方式进行计算和仿真分析。但实际上，车辆并不是质点，而是具有一定尺寸的物理模型，采用质点模型来估计车辆的安全距离往往存在一定的误差。尽管质点模型可用来进行避撞系统的初步设计，但若要获得更加精确的车辆避撞的安全距离，还需进一步考虑车辆的外形尺寸，而在此之前，须对其避撞轨迹进行规划。

不失一般性，以转向避撞为参考进行避撞轨迹的规划。在转向避撞参考轨迹的设计过程中，同样假定车辆在采取转向避撞之前按直线行驶且车速保持不变，车辆初始侧向速度、纵向加速度及纵向位移和侧向位移均为零，前方障碍物为静止状态。此时，还需考虑车辆的侧向速度和侧向加速度等约束条件，参考路径采用五次多项式规划策略。在五次多项式参考路径中，设车辆的初始坐标为（x0，y0），避撞后的终点坐标为（xt，yt）。在路径的起点，车辆此时的侧向位移、侧向车速及侧向加速度均为零。此外，还可进一步考虑车辆避撞结束时刻的侧向位移、侧向速度和侧向加速度等约束条件。假定结束时刻的侧向车速和侧向加速度为零。避撞结束时车辆的侧向位移yt＝a，纵向移动距离xt＝b，此时的纵向移动距离即为通过质点模型所求解的最小安全距离。

五次多项式参考路径表达式见式（7），其中c为拟合系数［11］。

通过计算，可得五次多项式的参考路径为

图4为车辆以80 km／h车速行驶时，通过转向避撞方式1和转向避撞方式2在高附着路面上进行操纵，所对应的参考轨迹及其参考曲率。可以看出，尽管转向方式2比转向方式1所需的纵向距离更短，但其所对应的曲率更大。

4 考虑车辆外形尺寸的避撞模型

为简单起见，假定前车障碍物外形尺寸与本车相同，即两车车宽wA和wB均为2 m，质心离前轴距离Lf和离后轴距离Lr也均为2 m。为使车辆在避撞过程中不与前车障碍物相互刮擦，还需考虑车辆外形尺寸的约束条件。同样，不失一般性，以转向避撞为例，车辆避撞约束示意如图5所示。

制动避撞相对较简单，与质点模型相区别的是，只需考虑本车质心至前轴的距离即可。转向避撞相对复杂，一方面要跟踪前小节所预先规划的五次多项式参考轨迹，同时还需满足相关的安全约束条件。对于安全约束条件的假定有多种，如有采用矩形安全区域的［7］，也有采用包络圆的［8］。本文采用与文献［4］相同的约束条件，即当车辆质心通过障碍物后端正上方时，由于车辆实际轨迹与预先规划的参考轨迹有可能不是完全一致，需保证车辆质心与离障碍物最近角点的距离大于一定的安全距离即可。以车辆左转向避撞为例，当车辆质心A点位于前方障碍车辆角端B点正上方时，AB两者的距离须大于等于两车宽的一半加上一定的安全距离d，本文取d值为0.5 m。

通过上述安全约束条件，可得以下关系式：

联立式（9）（10），可求出A点的x坐标，即为考虑车辆外形尺寸安全约束下的最小纵向距离。

图6（a）和（b）为车辆分别以80、100 km／h初始车速在高附着路面条件下，通过转向避撞方式1进行预定参考轨迹下的避撞效果。可以看出：当车速为80 km／h时，考虑车辆外形尺寸及安全约束条件下，与质点避撞模型下换道侧向位移为车道宽度约束条件的情况相比，最小安全距离可由原来的29.7 m减小为18.37 m；当车速提高到100 km／h时，最小安全距离可由37.12 m 减小为22.96 m。

图6（c）为车辆以80 km／h车速在高附着路面条件下行驶时，转向避撞方式1和转向避撞方式2进行预定轨迹下的避撞效果对比。其中，A1车、B1车为转向避撞方式1的效果，B1′车的后端点x坐标值为相应条件下采用质点模型所需的纵向距离；A2车、B2车为转向避撞方式2的效果，B2′车的后端点x坐标值为相应条件下采用质点模型所需的纵向距离。可以看出：采用转向避撞方式2，车辆避撞所需的最小安全距离可进一步缩短，即由18.37 m减小为12.99 m。

图7 （a）、（b）为车辆分别以80、100 km／h初始车速在低附着路面条件下，通过转向避撞方式1进行预定参考轨迹下的避撞效果。可以看出：当车速为80 km／h时，考虑车辆外形尺寸及安全约束条件下，与质点避撞模型下换道侧向位移为车道宽度约束条件的情况相比，最小安全距离可由原来的48.5 m减小为30 m；当车速提高到100 km／h时，最小安全距离可由60.6 m减小为37.5 m。图7（c）为车辆以80 km／h车速在低附着路面条件下行驶时，转向避撞方式1和转向避撞方式2进行预定轨迹下的避撞效果对比。可以看出：采用转向避撞方式2，车辆避撞所需的最小安全距离可进一步缩短，即由30 m减小为21.21 m。

图8 为车辆在不同避撞方式下，分别以不同车速行驶时所需的最小纵向距离。其中，图8（a）为在高附着路面条件下的对比情况，图8（b）为在低附着路面条件下的对比情况。结合图3可看出：与质点模型类似，制动与转向联合方式下的避撞所需的最小纵向距离比相应的纯转向方式有进一步的降低；同时，考虑车辆外形尺寸与安全约束条件下的避撞，与质点模型下换道位移为车道宽度的约束条件相比，车辆避撞所需的最小纵向距离也有进一步的减小。

5 结论

1）不管是质点避撞模型，还是考虑车辆外形尺寸的避撞模型，制动与转向最佳组合方式下的避撞效果均比相应纯转向的避撞效果要有所提高，即所需的最小纵向距离有所降低。

2）含有转向避撞方式2的避撞策略相比含有转向避撞方式1的避撞策略，所需的最小纵向距离进一步降低；但与此同时，其避撞过程也更加剧烈，即避撞参考轨迹的曲率更大。

3）考虑车辆外形尺寸的避撞模型更具有实际意义，在本文给定的安全约束条件下，与相应质点模型在换道位移为车道宽度约束条件下的情况相比，其所需的最小纵向安全距离进一步降低。

4）不同的避撞方式对于智能汽车自动紧急避撞系统的设计及自动驾驶研发均有重要意义，具体采用何种避撞策略取决于外部障碍物的具体位置和速度等约束条件，以及避撞系统设计者的主观倾向。

车辆动力学稳定约束条件是智能汽车自动紧急避撞系统设计须考虑的另一重要因素，后续将进一步结合车辆动力学模型，探讨不同安全距离模型对车辆避撞系统稳定性的影响。