切割路径优化问题的自适应大邻域搜索退火算法

吴 哲，徐圣伦，杨春梅，赵 帅，秦广义，李 超

（东北林业大学 机电工程学院，哈尔滨 150040）

在这个高速发展的科技时代，制造业技术时刻在更新，汽车行业车体的主要结构是钣金，要更快提高钣金车体的加工效率，加强切割工艺是一种很好的方式。钣金件的切割工艺是工业中常见的成形工艺，利用氧燃料、等离子体和激光热切割技术进行成形的工艺也非常普遍。加工和切割操作都涉及切割结束点的刀具重新定位到新切割开始点的操作，这种重新定位的刀具操作在每一个加工操作中要重复几次［1-2］。在机械加工过程中，刀具在每个切削周期中的重新定位的过程称为空行程，这种非生产性加工时间的最小化在高速加工的批量生产中起着重要的作用。

提高切割效率的最好方式是对刀具的切割路径进行优化。刀具路径优化的早期研究主要集中在钻削、掏槽和铣面等加工的快速运动和加工的局部运动［3］。通过优化切削参数、刀具顺序和使用的刀具路径类型，求解出工作过程中的最快加工时间，许多研究人员都对此进行了研究。Castellino等［4］对非生产性加工时间的最小化进行了研究，他们的研究是基于Ascheuer［5］对有约束的问题采用顺序排序启发式算法和Helsgaun［6］对无约束的问题采用LK 启发式算法的理论；Oysuand［7］针对刀具路径优化问题，提出了一种基于遗传算法的最小路径搜索算法，该算法成功地优化了切割特征点的数量和总工作时间；为了优化切割或焊接行程，Koenigand［8］高效地应用了很少使用的Lin-Kernighan算法，他们的程序集能够在2 s内计算出100个位置问题的优化刀具路径；Qudeiri等［9］利用遗传算法优化数控机床的操作顺序，还解决了一个作为非对称TSP问题的切割问题。

为了解决激光切割路径优化问题，本文提出了一种自适应大邻域搜索退火算法。该算法结合具有回火操作的模拟退火算法和自适应大邻域搜索算法中的破坏与修复操作。通过GTSP-Lib数据库中的实例进行了测试，与已知最优解进行对比，验证算法的精确性；又将算法运用到实际切割操作中，得出了优化路径，并将结果与最新的解决方案进行了比较，来验证算法的性能。

1 钣金切割问题的模型建立

1.1 钣金切割问题表述

在零件轮廓的完整切割中，激光束通过在轮廓的给定轨迹上移动，到在激光束返回到切割特征点之前在轮廓周长上或其附近打通一个特征点来开始切割［10］。由于激光器始终打开并在整个过程中进行连续切割，因此被认为是有成效的工作状态。相反，当激光切割头在关闭的情况下从一个切割特征点移至另一个切割特征点时，这是非生产性的工作状态，也被称作空行程。图1描绘了一个切割路径的示例，该路径具有嵌套在金属板上的9个不规则部分，粗实线表示从起始点开始的非生产性移动，每个轮廓上的小点表示切割特征点。如图1所示，切割顺序和切割特征点的位置会严重影响该行进路径的总长度，必须通过确定合适的打孔位置以及切割顺序，将这种非生产性的运动减至最少。

1.2 数学模型

本文中涉及的切割路径问题被表述为GTSP问题，其中预先定义了零件轮廓的所有特征点坐标作为潜在的打孔位置。为了确定最佳的打孔位置和切割顺序，对路径距离进行优化。通过考虑GTSP的整数规划，引入二进制变量xe∈｛0，1｝和yi∈｛0，1｝，其中e∈E和i∈V表示一条边e和一个节点i是否包含在切割轮廓中［11］。这个GTSP问题的一个可行解可以记作m条边的循环，所有的边连接在一起，每个边只有一个打孔点。因此，GTSP可以表示为整数规划，目标函数为：

目标函数服从于：

式中：ce是边缘轮廓e＝（i，j）的耗费距离；Vk是种群k中的节点；目标函数δ（v）＝｛e＝（i，j）∈E｜i∈S，j∉S｝描述了生成路径的成本。约束条件1（式（2））确保从每个轮廓／群集中仅选择一个打孔点；约束2（式（3））用于强制每个轮廓的起始点和结束点位于同一位置；约束3（式（4））是消除子路径（S）路径约束的限制，即子集上的路径少于n个节点。最后，约束4（式（5））和约束5（式（6））是使函数成立的二进制变量条件。

2 算法的设计与实现

本节从算法框架、邻域搜索操作、终止条件判定3个方面展开研究，重点设计了结构清晰且功能模块相对独立的自适应大邻域搜索算法框架，对搜索算法中的破坏算子和修复算子进行了改进，并通过改进的模拟退火算法对算法进行接受准则判定，实现高精度的全局搜索的自适应大邻域搜索退火算法构建［12］。

2.1 自适应大邻域搜索算法框架

GTSP作为一类基础的路径优化问题，在各种相关工程问题上都有所涉及。要想在特定问题上找到相对合适的特定算法，需要在原有的算法框架上进行构建。自适应大邻域搜索算法具有搜索范围广和操作模块较为独立的特点，因此通过构建算法框架将算法模块化，然后对内部模块进行改进，设计更加适合的算法。

如图2所示，根据算法框架确定改进的核心思想是：在定义好初始种群的情况下，通过改善邻域搜索操作中的算子，使算法更快地产生新解，以数值优化为目标接受更优解，对新解进行多次迭代达到最优。将算法分解成独立的功能模块，便于明确各模块目的来进行程序设计。再运用优化判定准则，在多约束条件下获得更好的全局搜索。

2.2 改进邻域搜索算子的ALNS算法

自适应大邻域搜索算法（ALNS）是从大邻域搜索算法（LNS）发展而来的，两者的算法框架是相同的，都是通过破坏和修复操作算子来获取解的邻域。ALNS在LNS的基础上，允许在同一个搜索中使用多个破坏和修复操作，ALNS会为每个破坏和修复操作分配一个权重，通过该权重从而控制每个破坏和修复操作在搜索期间使用的频率。在搜索的过程中，ALNS会对各个破坏和修复操作的权重进行动态调整，以便获得更好的邻域和解。ALNS通过使用多种破坏和修复操作，然后再根据这些破坏和修复操作生成的解的质量，选择那些表现好的破坏和修复操作，再次生成邻域进行搜索。其简要伪代码如下：

算法1ALNS算法

上面就是ALNS伪代码。在代码第2行，定义了破坏和修复操作的权重集合，开始时所有操作都设置相同的权重。Ω1和Ω2分别表示破坏和修复操作的集合，根据ρ1和ρ2选择破坏和修复操作。至于选择哪个操作的可能性大小，由下面公式算出：

由式（7）可得，权重越大，被选中的可能性越大。除此之外，权重大小是根据破坏和修复操作在搜索过程中的表现进行动态调整的。

在ALNS算法的每个循环的迭代中，都要经过一次破坏和修复操作，不同的操作对算法的优化程度有着很大的影响，在进行破坏操作时，选取的删除方法是统一最坏删除方法。在统一最坏删除过程中，先给定一个集合T使VT＝｛v1，v2，…，vl｝，删除顶点vj使删除成本最大化：

其中指数j-1和j+1用l+1≡1和0≡l进行评估。也就是说，删除了导致路径长度减少最多的顶点，因为它可能在计算中被放错了位置。在统一最坏删除方法中，通过删除代价rj来拓展这一思想，这将创造一系列通过参数化λ的删除方法。特别是：

1）λ＝1时对应随机删除，其中顶点Nr从集合VT中均匀随机选择删除。

2）λ＝0时对应最坏删除。

对于λ∈（1，∞）的值，获得了随机化程度不同的最坏删除的随机方法，类似于Ropke［13］提出的随机化方法。每次删除可以在O（m）次内完成，因此Nr的清除需要O（Nrm）次。

在修复操作中也有很多的插入方法，本文选取的是统一插入方法。先给定一个带有V的分区PV∶｛V1，…，Vm｝和坐标G＝（V；E；w），将部分GTSP循环定义为G中的一个循环，这样分区PV中的每个集合最多只访问1次（在一个完整的循环中，每个集合只访问1次）。给定一个局部历程T＝（VT；ET），T访问的分区集合记为PT⊆PV。

剩下的就是指定选择插入集合（Vi∈PV＼PT）的机制。对于每个集合Vi，i∈｛1，…，m｝和每个顶点u∈V＼Vi，计算距离为：

基础的插入方法有最近插入方法、最远插入方法和随机插入方法3种方法：

最近插入方法会选取包含顶点v的集合Vi，该集合为距局部路径T的顶点的最小距离。选择集合Vi的方法为：

最远插入方法选择顶点与部分路径T上的顶点最接近的集合Vi，选择集合Vi的方法为：

随机插入方法是从PV＼PT中随机抽取1组集合Vi。

最近插入方法、最远插入方法和随机插入方法可以集合成统一插入方法。给定一个局部路径T，接下来可以插入集合PV。对于每个集合Vi∈PV＼PT，将Vi和T之间的最小距离定义为：

给定参数λ∈［0，∞）和部分路径：

1）通过设置λ＝1获得随机插入方法；

2）通过设置λ＝0获得最近插入方法；

3）通过设置λ＝+∞（或足够大）获得最远插入方法。

此外，通过选择的中间值，可以获得最近、最远和随机插入的随机化版本，从而允许在大型邻域搜索区间对解进行更大的探索。

2.3 改进模拟退火算法判定接受准则

自适应大邻域搜索算法的接受准则和停止准则有很多种，有最简单的直接根据目标值来判断，也有通过各种复杂的模拟退火降温冷却等过程来判断。但这些方法都存在准确性差、鲁棒性弱的缺点，本文选用的判断接受准则是在基础模拟退火算法的基础上进行改进得到的。

模拟退火算法是通过控制参数T按降温函数T（k+1）＝kTk降温，使其值逐渐下降直至变为零。在T值逐渐变小的过程中，算法跳出局部最优的能力越来越弱，当T值降到充分小时，算法完全丧失跳出局部最优的能力，使所求结果准确性下降［14］。

根据热力学原理，在温度为T时，出现能量变化ΔE的概率为X（t），表示为：

其中k是常数，且ΔE＜0（能量总是降低的）。式（13）表明：①温度越高，出现降温的概率越大；②温度越低，出现降温的概率越小。

又由于ΔE总是小于0，因此ΔE／kT＜0，exp（ΔE／（kT））取值是（0，1），那么X（t）的函数取值范围是（0，1）。

在模拟退火算法运行前期，温度值T较大，降温概率X（t）高，算法很难达到局部最优；但随着算法运行到后期，T值变得较小，降温概率X（t）也随之变小，算法最终变为局部搜索，并陷入局部最优。要避免陷入局部最优，需要通过Metropolis准则进行判定。

Metropolis准则常表示为：

从式（14）可以看出，若En+1＜En（即移动后可以获得更优解），则总是接受该移动；若En+1≥En（即移动后的解比当前解要差），则以一定的概率接受移动，这个概率会随着温度变化逐渐降低。通过Metropolis准则，可以在陷入局部最优后进行较差值的接受，以此来跳出局部最优，若跳出后能发现更优解，则从局部搜索再次变为全局搜索。

要提高整个算法获得的最终解的质量，应该避免算法过早地陷入局部最优。在运算初始，算法具有较高的温度T，算法的接受率高，但随着温度T的降低，算法的接受率越来越差，不可避免地会变为局部寻优问题。只有在温度降为0后，重新提高T值，才能使算法的接受率再次提高，从而获得全局最优解。这种操作称为模拟退火算法的回火操作，回火后再重复进行模拟退火算法，就有可能得到全局最优解。

在初始定义参数时，加入参数回火结束温度Tc和回火系数b，在退火操作后，重新回火至初始温度，缓慢降温，直到温度降至Tc，结束回火阶段。因为回火操作重复退火时的计算过程，进行多次会极大地增加计算时间，所以选择5～10次较为合适。初次回火时的初始解为上次退火时的最终解，之后每次回火操作都以上次退火的最终解作初始解。

改进模拟退火算法的具体步骤如下：

步骤1给定退火初始温度T0，初始解状态x，定义记忆器best，退火终止温度Tf，退火系数a，回火系数b，回火结束温度Tc，马尔可夫链长度Lk，k＝0；

步骤2k＝k+1，当k≥Lk时，转步骤12；

步骤3对个体x进行个体邻域搜索算法，生成新的初始解x′；

步骤4计算能量的增量ΔE＝f（x′）-f（x），其中f（x）为评价函数；

步骤5若ΔE＜0，则接受x′为新的初始解，即if（ΔE′＜0），x＝x′转步骤7；

步骤6若ΔE≥0，通过Metropolis准则进行判定，接受达到概率的新解x′；

步骤7Tk+1＝a·Tk，对退火温度进行重新定义；

步骤8if（Tk≤Tf），退火终止；

步骤9进行回火操作，回温到初始温度；

步骤10Tk′＝b·Tk，对回火温度进行重新定义；

步骤11if（Tk′≤Tc），回火终止，转步骤2；

步骤12输出最终解best＝x，算法结束。

在回火过程中，最高温度随着每次回火而逐渐下降，直至达到回火终止温度，算法停止。在回火过程中，算法接受最优解的能力将得到提高，这对于获取最优解是有益的。

事实上，回火操作早期有着较高的回火温度，算法对较差值的接受能力也很高，能很好地扰乱当前解，迫使算法程序继续移动，从而获得很好的解。而当算法进行到后期时，回火温度开始变低，算法的结果越来越趋近于最优解，最终将回火温度控制在有效域区间，再通过退火操作对较优解进行保留，经过比较后求得最优解，以此来平衡局部搜索与全局搜索，使算法的性能得到增强。

在时间复杂度上，普通的模拟退火是O（n2），面对小规模的问题时，效率和准确性极高。但随着数据规模的增加，计算量增大的同时却不能带来较好的准确性。而本文的改进算法只需要增加回火次数M和插入删除操作次数N，最终时间复杂度为O（MNn2），与普通的模拟退火属于相同的量级，但在准确性上得到了极大的提高。

3 实验与分析

3.1 激光切割路径优化

为了验证上文中提出的自适应大邻域搜索退火算法的可行性，在WindowsWin10，CPU 3.4 GHz，8 GRAM，Matlab2016a的开发环境下进行激光切割路径优化。在进行切割路径优化前，先通过GTSP-Lib数据库［15］中的几个二维笛卡尔算例进行测试，并对改进算法求得解与数据库最优解进行对比，结果见表1。

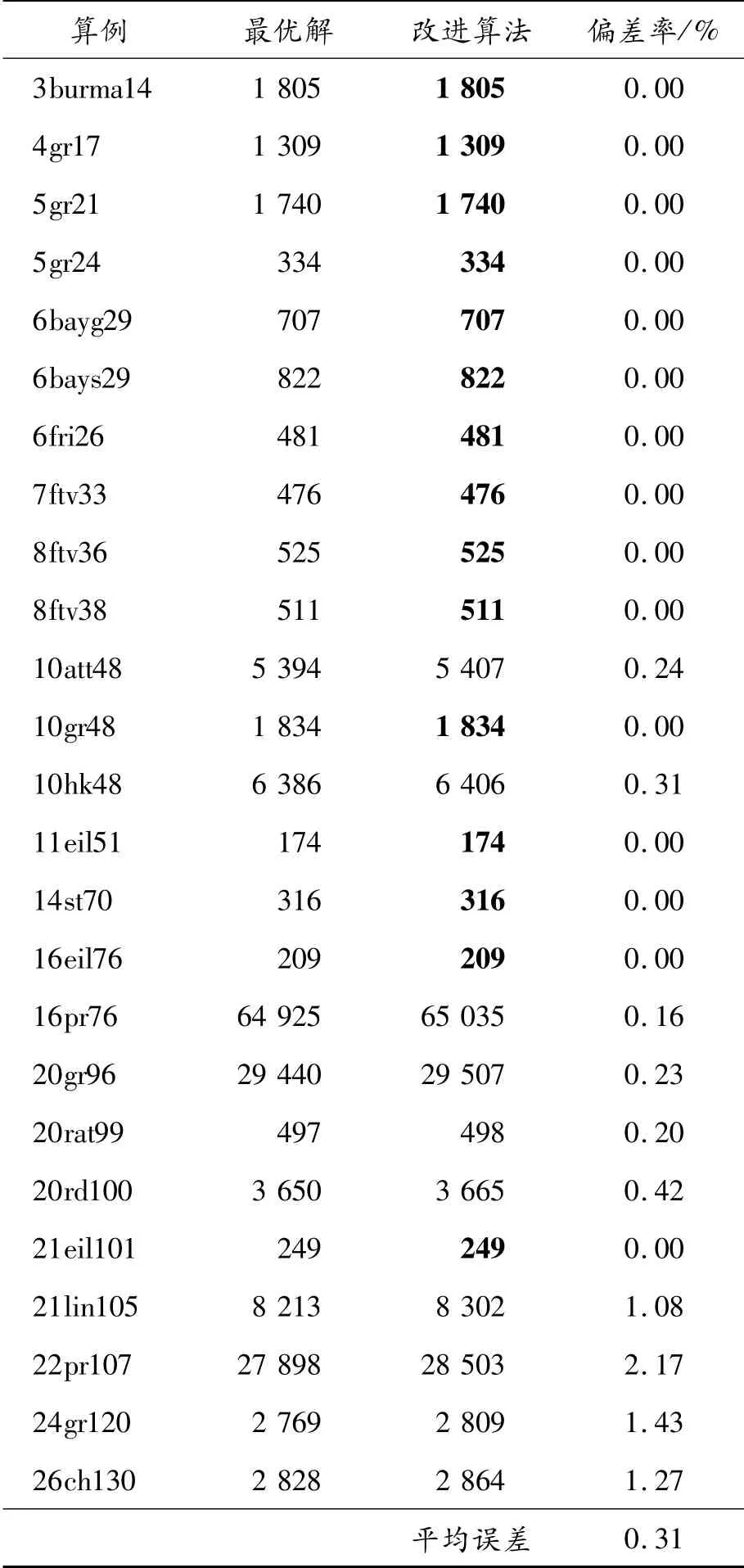
表1 GTSP-Lib数据库算例测试结果

该算法求解了25个来自GTSP-Lib数据库的算例，结果如表1所示，达到最优解的解用黑体表示。通过对比发现，在解决小对象规模问题时，该算法具有较好的求解质量，与已知解相比，平均误差仅为0.31%。随着对象规模的增加，最优解获得概率和求解效果都有所下降。对达到最优解的算例14st70进行分析，得到的具体优化路径如图3所示。图4是经过分析后的优化过程曲线，细线表示优化运算中的路径当前值，粗线是通过运算可以得到的较优解。算法每次迭代后都会记忆退火操作后的较优解，通过改变每次迭代的破坏和修复方法和更优解接受规则，实现了搜索范围的逐步收缩，由大邻域逐渐缩小至最优解，并且每次退火运算后，结果都能够得到很大程度的提升。

表1中数据来自于GTSP-Lib数据库，其中计算偏差率＝［（改进算法-最佳解决方案）／最佳解决方案］×100%。通过数据可以发现，改进算法在求解小规模问题时，精确度极高，几乎没有误差，平均最优解获得率达到90%。但当问题规模大于45个种簇时，算法性能开始下降，平均最优解获得率变成70%。这种性能减弱在处理大问题时特别明显，这是因为问题大小的增加放大了可能的解决方案的数量，从而延长了运行时间，降低了算法解决性能。在有限实验次数中的最优解数值并不能完全反映算法性能，因此通过偏差率来评价算法的普遍求解效果，如表1所示。自适应大邻域搜索退火算法的平均偏差率为0.31%，整体计算结果与最优解的相差较小，即表明算法每次求解能够大概率获得一个较好的解，适用于次数较少的运算过程。总的来看，自适应大邻域搜索退火算法不仅获得了大部分算例的最优解，求解精度令人满意，而且整体偏差率较小，鲁棒性好。

3.2 针对实际样板切割实验

本文采用高速数控激光加工机床进行实验，参数设置为：切割速度为1 000，加速度为8 000，减速度为8 000，操作系统界面如图5。

切割样式通过CAD制图导入操作系统，在CAD上先绘制排版好的零件版图，如图6所示。图中的实例是由全封闭图元组成的图形，图中共有18个封闭图元，每个图元都有独立的标号，是作为图元读取时设定的记号，用来区分各个图元。封闭图元切割的起始点与结束点相同，保证有效切割，减少工作性切割损耗［16］。

本研究针对图6全封闭图元组成的实例，分别用本文提出的自适应大邻域搜索算法和Stephen L.Smith［17］提出的GLNS算法进行优化。进行10次实验，分别记录下得出规划路径的时长和路径总长度，详细数据见表2。由表2可得出，优化后的最佳路径长度为6 657 mm，得到的最优解用黑体表示。通过对比可以发现，本文提出的自适应大领域搜索退火算法在准确性上与最新提出的GLNS算法大致相同，但计算时间有所减少，提高了计算效率，表明了该算法在解决复杂轮廓切割路径规划问题上较为稳定，也验证了算法在解决这类GTSP问题时是可行的。

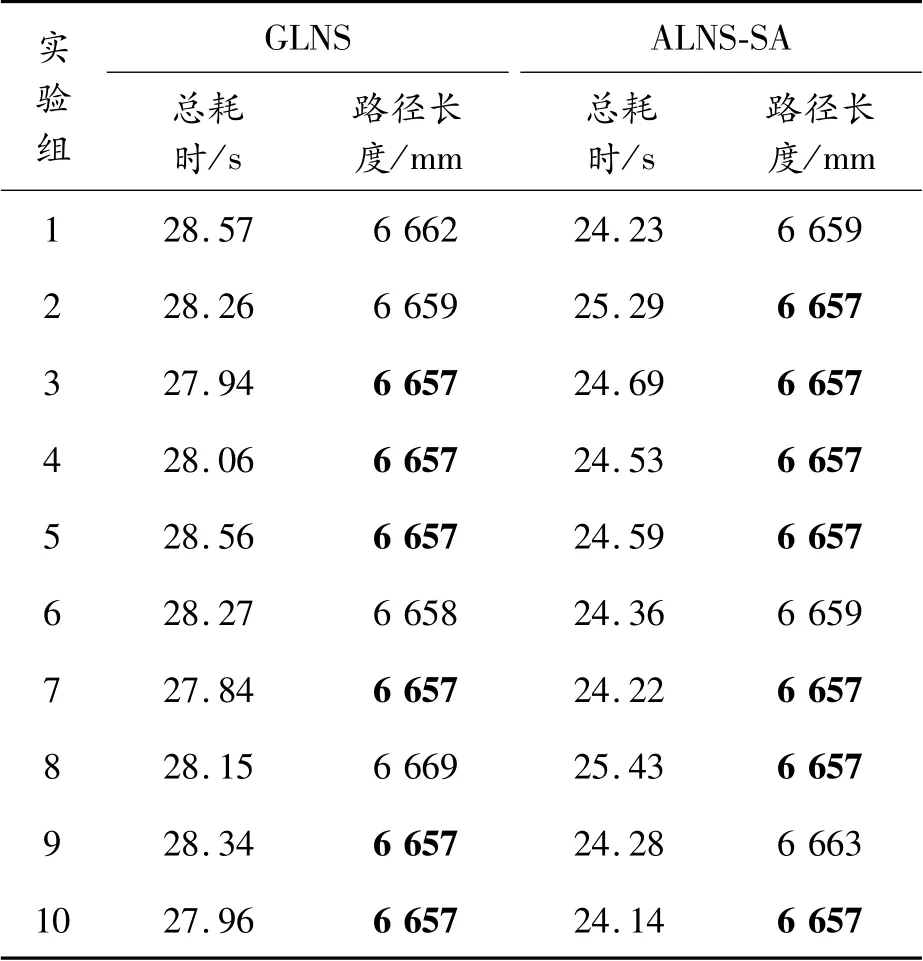
表2 排样规划路径参数对比

4 结束语

为了解决激光切割过程中的路径优化问题，提出了一种自适应大邻域搜索退火算法，该算法是一种启发式算法，它以自适应大邻域搜索退火算法（ALNS）为基础，通过统一最坏删除方法和统一插入方法进行破坏和修复操作的改进，再以改进模拟退火算法作为接受准则。所提出的算法已通过GTSP-Lib的各种实例进行了测试，其结果与现有的最著名解决方案相比较，平均误差仅为0.31%。当使用该算法解决切割路径实例时，在保证准确率的情况下，运算效率得到了很大的提高。因此，该算法将成为解决激光切割过程以及其他机械制造操作中的路径优化问题的一种优势算法。