机场出租车载客优化模型*
王欣颖,欧 辉,李 婧
(湖南师范大学 数学与统计学院,湖南 长沙 410081)
1 引 言
近年来,随着科学技术的不断进步和人们生活水平的不断提高,乘坐飞机逐渐成为一些人首选的出行方式,民用航空运输量不断增长,大多数乘客下飞机后要去市区或周边目的地,这就给机场多元化的交通方式带来了较大的压力.机场陆侧交通系统在衔接机场交通和城市交通中占据了主要地位,其中出租车以其灵活便捷的特点,在众多交通工具中发挥着不可替代的作用.
针对机场出租车的有关问题,近年来已开展过相关研究.耿中波(2013)[1]建立了基于VISSIM微观交通仿真的比选方法,提出小时通行能力、对环境影响和旅客感知三个评价指标,并根据仿真结果对备选方案做了综合评价.黄岩(2014)[2]通过对调查获取的交通参数进行分析,围绕如何提高既有交通设施通行能力,对出租车上客点的组织管理方式进行研究,从而为出租车上客点设计及运营效率提供参考和借鉴.孟维艳(2014)[3]提出釆用智能场站技术构建一个将视频识别、联网监控、智能诱导、运输管理融合为一体的机场出租车场站管理系统,并实时联网,实现对机场候客出租车的有序管理.颜超(2015)[4]以三种类型的枢纽机场陆侧交通管理组织方式为切入点,提出了以新公共服务理念为导向建立一体化公共交通系统、以协同理论为基础做好停车资源利用与路网规划和以服务公众为目的提升陆侧公共交通服务水平的观点.Meryemn(2016)[5]通过网络数据包络分析方法得到了一个拥有动态组成部分的结果,探究了不同公司效率不同的原因.胡稚鸿(2019)[6]引入GPS识别轨迹的方法,以科技手段维护公平、合理、有序的运营环境.这些研究都是从维护机场秩序和减少乘客等待时间出发的,鲜有针对出租车司机收益的最大化角度建立的优化决策模型.
以出租车司机利润为研究目标建立优化决策模型或许是有价值的.
2 研究方法
2.1 相关性分析
对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素的相关密切程度.利用SPSS软件对数据做Pearson相关性分析,研究决策对各因素的依赖性,判断决策结果与各因素是否有显著的相关性.
2.2 排队论
研究系统随机聚散现象和随机服务系统工作过程的数学理论和方法,又称随机服务系统理论.排队系统主要由输入过程、排队规则及服务机构组成.借助多服务窗等待制排队模型,即M/M/n排队模型,对乘客与出租车进行合理的资源配置,并结合VISSIM仿真模拟软件,设计出最佳上车点.
2.3 动态规划
运筹学的一个分支,求解决策过程最优化的数学方法.把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解的方法.
2.4 分析工具
(1)SPSS:统计分析,进行Pearson相关性检验.
(2)VISSIM:基于时间间隔和驾驶行为进行仿真建模,通过设置车道各项数值、乘客乘车的时间、交通信号等指标,进行仿真模拟测试.
3 决策模型的建立及检验
由于国内多数机场都是将送客与接客通道分开的,送客到机场的出租车司机都将会面临两个选择:一是前往到达区排队等待载客返回市区,依“先来后到”排队进场载客,会付出一定的时间成本;二是直接放空返回市区拉客,则会付出空载费用和可能损失潜在的载客收益.
从乘客交通方式的选择、客流量、天气等角度出发,将决策问题转化为以时间为基准的利润比较,从而建立简洁直观的出租车司机决策模型.
对于乘客可以选择的交通方式,除了出租车还有机场大巴、磁悬浮及地铁.而乘客的选择主要受时间点、天气以及机场所处位置的影响.为分析出租车司机的决策,需要分析其他另外两种竞争性的交通方式.
1)机场大巴
经过收集相关数据,得到长沙黄花国际机场大巴运行时刻如表1所示.

表1 机场大巴时刻表
由表1可以看出,虽然机场大巴时刻表与总体航班时段吻合,但是往往结束的比较早.
2)磁悬浮及地铁
经过数据收集(数据来源:长沙市轨道集团官网http://www.hncsmtr.com/),得到长沙市地铁和磁悬浮列车首班车均在6:30左右发车,末班车22:30.故机场地铁起始时间相比于机场大巴运行时间更长,但仍有部分时段的乘客无法选择此交通方式.
显然,乘客可选择的其他交通工具越少,选择出租车的可能性则越大.亦即机场其他交通方式的运行时间影响着乘客对出租车的需求和出租车司机的决策.一般来说,夜间回市区选择出租车的乘客的比例更大,白天相对来说会小一些.
另取长沙黄花国际机场周一的航班信息作为分析数据,根据机型查阅座位资料得到各时段客流量如表2所示(假设每个航班都是满员).

表2 对应时刻客流量
天气作为一个不确定性因素也影响着出租车司机的决策,同样需要进一步的研究.对于不利于人类活动的天气,人们往往会选择更为方便的交通工具代替出行.同时天气因素也会对交通产生极大的影响,容易造成交通堵塞等现象,尤其对于公交车等公共交通工具来说,出租车能够灵活地选择更优的线路,能提高出行效率.
对于不同的天气情况,人们做出的选择往往也是有明显的差异的.分析天气因素时,主要考虑以下几个因素:气温、天气状况、风力.通过分析三者间的关系,指定一个总评分值.天气状况的具体数值转换标准[7]如表3所示.

表3 天气数值转换标准
由于极端天气出现的概率较低,故不列入考虑范围中.以q表示天气最终得分,e为天气状况评分数值,w为温度数值,f为风力评分数值,通过对天气状况、气温、风力三种天气因素进行定性和定量分析,在不断修正后得到天气最终得分q的表达式为
q=e+(30-|20-w|)+f.
综上所述,出租车司机决策模型的建立主要从天气因素和时段因素来考虑.飞机入港时间将影响到乘客的选择,公共交通工具的停运将极大程度的提高乘客对出租车的需求,可以认为夜间时段里乘坐出租车的乘客比例比白天多出30%.而关于天气得分的分析如下:天气得分越高越适合人类活动,故选择出租车的乘客比例会变小;天气得分越低越不适宜人们出行,因此选择出租车的乘客数量将增加.最终得到天气得分对乘坐出租车乘客比例的影响方程为
f(q)=a0+a1×cos(q×ω)+b1×sin(q×ω),
其中:a0=-3550999.1,a1=3531000,b1=-1430,ω=0.000004196.
故建立出租车司机的决策模型为
F(t1)=wB-wA=(w1t1-p0t0-p1)-(w0-p0t0-p1)=w1t1-w0,其中t1为在蓄车池内等待时间,t0为平均等待时间,w1为市区载客平均净收益,w0为机场至市区送客总收益,p1为机场至市区路段油耗成本,p0为时间成本.
由决策函数F(t1)的意义可知:
1)当F(t1)>0时,wB>wA,此时出租车司机选择决策1,
2)当F(t1)≤0时,wB≤wA,司机选择决策2.
为检验上述模型的准确性,于2019年8月进行了实地检验,利用长沙每天的天气状况信息计算各日的天气最终得分,与司机各项指标一同带入模型,确定决策,部分结果如表4所示.

表4 各项指标及司机决策
分析结果可知,随机生成的31组数据中有14组决策是A,17组决策是B,可见在各种随机出现的情况中,不会出现“一边倒”的情况.
为了进一步探究各个影响因素对出租车停车等候时长的影响,借助Pearson分析方法,利用SPSS软件研究决策对其他因素的依赖性,对表4中的随机指标数值进行分析,并用0、1代替决策中的A、B,其中等待时间与决策的相关性分析结果如表5所示.

表5 Pearson相关性分析结果
其中P值小于0.05,表明相关性显著.反映了决策结果对其影响因素的依赖性.
4 上车点的设定优化
在某些时候,经常会出现出租车排队载客和乘客排队乘车的情况.长沙黄花国际机场乘车区现有两条并行车道,基于排队论的方法,利用VISSIM软件进行仿真模拟,从机场管理部门的角度设计合理的“上车点”,在保证车辆和乘客安全的条件下,使得总的乘车效率最高.
在输入过程中,机场乘客到达乘车区的方式可以是逐个或成批.乘客到达乘车区时两条车道均可等待,并按照先后顺序排队等待上车.在两条平行车道上,乘客排队是一种串列或并串同时存在的混合排队.因此得出该排队系统为多服务窗等待制排队模型M/M/n.
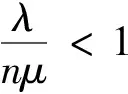
假设没有乘客流失的情况,可以得到以下目标变量:
系统绝对通过能力a=λq=λ(q=1),
平均排队等待的乘客数
乘客排队等候的时间的均值
来到系统的顾客必须排队等待的概率
考虑到乘客的排队速率、安全问题以及出租车的排队效率,利用VISSIM软件优化上车点分布的仿真[8],最终确定设定四个乘车点.设计图和仿真模拟图分别如图1、图2所示,即在并行车道的一侧分别设置出租车和乘客等候区,车辆选择进入到候客区A、B蛇形排队等候载客,与此同时在等候区A、B之间设立乘客等待区.乘客由机场工作人员指挥依次排队候车,在车辆候客区靠近并行车道的位置设置上车点,每区两个.并规定在A区等待的出租车在接到乘客后从左侧车道驶离机场,而B区等候的司机则需从右侧车道驶离.

图1 上车点设计图

图2 仿真模拟图
5 短途载客的补贴设计
机场出租车载客收益与载客行驶里程有关,乘客目的地有远有近,有的远途乘客目的地在市区,而有的短途或中短途乘客的目的地则可能是附近郊区.出租车司机载短途客人后若再回到机场排队接客可能收益不大.假设司机不能选择乘客也不能拒载且允许多次往返载客.为尽量均衡这些出租车司机的收益,机场管理部门应该对短途载客再次返回的出租车给予一定的“优先权”,设立短途再次返回车辆快速通道.
下面针对快速通道所应优先缩短的时间t进行计算分析,求出最合理的设计.
经过数据的搜集,得到长沙出租车收费标准如表6所示.

表6 长沙出租车收费标准
假设出租车始终匀速行驶,车速为v千米/小时,燃油费用为a元/千米,p1、p2、ps、pl分别为短途2千米内、短途2千米至13千米、短途接单以及长途接单的概率,t0为平均等待时间,x1和x2分别为长途里程数和短途里程数.可以得到以下不同的目标:
长途收益为
fl(x)=(3-2a)x1-9,x1≥13,
短途收益为
短途平均收益为
fs(x)=p1×f1(x)+p2×f2(x),
长途速率为
短途速率为
短途平均速率为
vs=p1·v1+p2·v2.
此时t满足补偿收入速率方程
根据查阅资料和实地考察得到的数据可知,平均车速v=50千米/小时,a=0.5元/千米,接单概率p1=0.2,p2=0.8,ps=0.1,pl=0.9,平均等待时间t0=0.25小时,长途平均里程数x1=36千米,由此快速通道所应优先缩短的时间t应满足
6 结 论
针对机场“车等人”和“人等车”的问题,建立了以时间为基准的利润最大化决策模型,并对模型进行了有关涉及变量与决策结果的相关性检验,确定了模型的可行性和合理性.基于排队论与动态规划的思想,针对机场乘车区内现有的两条并行车道,进行了优化设计,在车道右侧设置出租车和乘客等候区及最佳上车点.制定了鼓励短途载客出租车返回载客的相关政策,即设立短途返回车辆快速通道.基于动态规划思想针对快速通道所应优先缩短的时间进行了计算分析.

