有干预措施的 Filippov戒烟模型的全局动力学*
马慧丽,黄立宏,王佳伏
(长沙理工大学 数学与统计学院 , 湖南 长沙 410114)
1 引 言
吸烟和接触烟草烟雾是全球公共卫生的一大威胁, 它引发了许多其他疾病并且造成了严重的发病率和死亡率, 如癌症、慢性肺病、心血管疾病和中风等.吸烟行为还具有可传播性和扩散性, 潜在吸烟者可能通过与吸烟者接触而吸烟.从某种意义上说吸烟行为与传染病有类似的传播机制.因此许多学者运用传染病传播原理建立戒烟动力学模型来预防和控制吸烟.如Carlos Castillo-Garsow(1997)等[1]利用传染病传播原理建立了一个 SIR 模型来研究戒烟问题, 并分析了所建模型的基本再生数及无烟平衡点和吸烟平衡点的稳定性.李志民等(2019)[2]建立了一类具有非线性发生率的戒烟模型, 并分析了其动力学行为.王霞等(2019)[3]研究了一类带有非线性接触率和戒烟不完全成功的戒烟模型, 并研究了该模型平衡点的全局动力学性质.考虑到媒体和政府对吸烟的干预作用, Sharma等(2015)[4]提出了一个非线性数学模型来研究媒体报道对戒烟的影响.Guerrero等(2011)[5]用一个流行病学模型来研究吸烟在西班牙人口(16-65 岁)中的流行演变规律, 发现在 2006 年西班牙无烟立法后在最初几年的实施中有非常积极的影响.
事实上, 大众媒体宣传可促进保护非吸烟者并劝阻人们使用烟草[6].由于众多经典的微分方程戒烟模型都是右端连续的, 但若考虑到媒体和政府的干预等因素, 建立右端不连续的戒烟模型或能更真实地刻画人们的吸烟行为.相比于用右端连续微分方程模型描述不连续的干预现象, 右端不连续的Filippov 系统不仅能够更准确地刻画这些不连续现象, 而且由于所建 Filippov 模型的不连续性, 使得系统具有更加丰富的动力学行为, 从而揭示出丰富且具有重要生物学意义的新结果.因此将Filippov系统运用到戒烟模型中,运用Filippov定性理论分析模型的动力学行为,从而可以得到政府和媒体干预对戒烟的影响.
2 模型的建立及预备知识
2.1 模型的建立
由于无烟情况是很难实现的,控制吸烟人数在一个合理的范围更加符合实际.在一些现有工作的基础上[1-5,7-17], 结合阈值策略, 提出式(1)所示的一个基于干预措施的 Filippov 戒烟模型来研究媒体和政府干预对吸烟传播的影响.
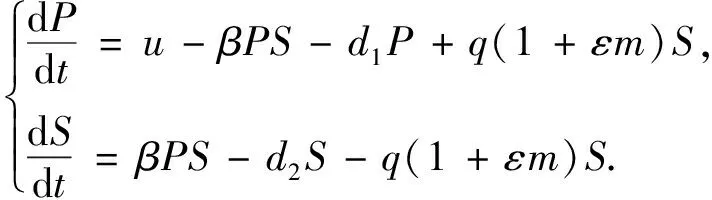
(1)
其中
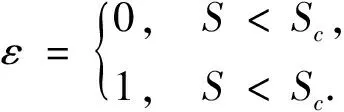
这里所有的参数均为正值.其中P=P(t),S=S(t)分别代表了潜在吸烟者和吸烟者的数量,μ表示潜在吸烟者的出生率,β代表潜在吸烟者与吸烟者的接触影响率,d1,d2分别代表了潜在吸烟者和吸烟者的死亡率,q表示戒烟率,m表示政府和媒体对吸烟的干预强度.
模型采取如下的阈值策略:
当吸烟者的数量低于临界水平Sc时, 不采取干预措施, 此时由于基本的健康意识, 一般情况下人们会有戒烟意识和措施, 戒烟率为q;
当吸烟者的数量超过Sc时, 政府和媒体采取干预措施, 减少吸烟人数, 提高戒烟率, 戒烟率为q.
2.2 解的正性和有界性
考虑到系统(1)的现实意义, 这一节讨论系统(1)解的正性和有界性.
引理1[10,15]设(P(t),S(t))是系统(1)满足初值条件P(0)≥0,S(0)≥0且定义在区间[0,T)上的解, 其中T∈(0,+].那么对所有的t∈[0,T),有P(t)≥0,S(t)≥0.
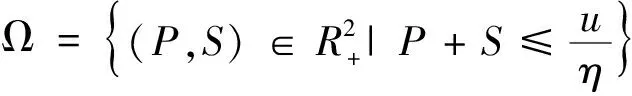
2.3 子系统动力学分析
这个部分主要分析子系统的动力学性质, 在区域G1和G2,系统(1)可以分成子系统(2)和子系统(3).
(2)

(3)
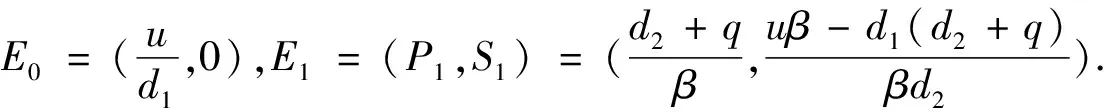
引理3当R1<1 时,E0是子系统(2)的全局渐近稳定的无烟平衡点; 当R1>1时,E1是子系统(2)的全局渐近稳定的吸烟平衡点.
证明系统(2)的 Jacobian 矩阵为
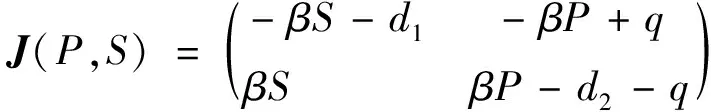
由特征方程|J(E1)-λI|=0知, 特征根为
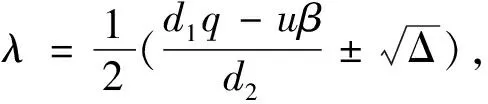
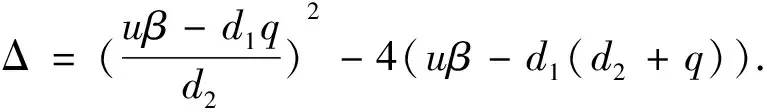
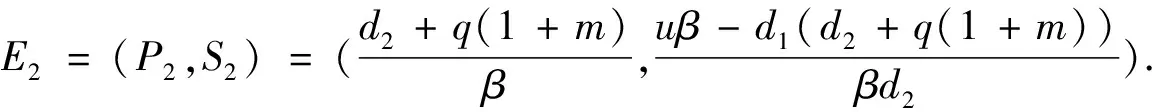
类似地, 采用引理3的证明方法可以得到下面的结论.
引理4当R2<1时,E0是子系统(3)的全局渐近稳定的无烟平衡点; 当R2>1时,E2是子系统(3)的全局渐近稳定的吸烟平衡点.
2.4 滑模域和滑模方程
本节讨论系统(1)的滑模动力学.
首先来讨论滑模区域的存在性.取法向量为n=(0,1), 由 〈n,F1(P,Sc)〉〈n,F2(P,Sc)〉<0可知滑模区域存在且为
Σs={(P,S)|P1 其中P1和P2分别为切点T1和T2的横坐标.根据 Filippov 凸方法[18]可知系统(1)在Σs上的滑模方程为 (4) 本节讨论系统(1)的全局渐近稳定性, 首先来排除系统(1)的闭轨. 图1 可能存在围绕的闭轨示意图 (5) 在区域D1内运用格林公式, 可以得到 因为A2>A1, 那么 图2 当E1为实,E2为虚时, 可能存在包含部分的闭轨示意图 引理7[18]如果系统(1)的正半轨T+是有界的, 那么它的极限集Ω(T)要么包含一个平衡点, 要么包含一个闭轨. 定理1当R1<1时, 系统(1)的无烟平衡点E0是全局渐近稳定的. 证明由于R2 f(P1)=-d1P1+u-d2Sc=d2(S1-Sc)<0,f(P2)=d2(S2-Sc)<0. 即f(P)<0当P∈(P1,P2), 这说明此时伪平衡点不存在.此外分别由引理1和引理2可知,系统(1)的解是有界的, 并且无任何形式的闭轨.那么根据引理7, 此时唯一的实平衡点E0是系统(1)的ω极限集, 即当R1<1时,无烟平衡点E0是全局渐近稳定的, 如图3所示. 其中参数取值为:u=3,d1=0.2,d2=0.6,β=0.02,q=0.1,m=4,Sc=7. 当R1>1时, 由于P1 定理 2 当R1>1时, 下面结论成立: (i)当0 (ii)当S1>Sc,S2>Sc时, 实平衡点E2是全局渐近稳定的; (iii)当S2 证明 首先来证明结论(i).当0 f(P1)=d2(S1-Sc)<0,f(P2)=d2(S2-Sc)<0. 即在区间(P1,P2)上f(P)<0, 这说明此时伪平衡点不存在.在系统(1)解有界并且无闭轨的情况下, 由引理7 可得出唯一的实平衡点E1是全局渐近稳定的, 如图 4 所示.类似地, 也可以得出结论(ii): 当S1>Sc,S2>Sc时, 实平衡点E2是全局渐近稳定的, 如图5所示. 图4 吸烟平衡点E1的全局渐近稳定的平面相图 图5 吸烟平衡点E2的全局渐近稳定的平面相图 接下来证明结论(iii).当S2 f(P1)=d2(S1-Sc)>0,f(P2)=d2(S2-Sc)<0. 此时函数f(P)在区间(P1,P2)上有唯一的一个零点P*,这说明滑模上有一个伪平衡点E*=(P*,Sc).由于在区间(P1,P*)上f(P)>0, 在区间(P*,P2)上f(P)<0, 那么伪平衡点E*在滑模上是稳定的.在系统(1)的解有界并且无闭轨的情况下, 可得出: 当S2 图6 伪平衡点E*的全局渐近稳定的平面相图 其中参数取值为:u=10,d1=0.2,d2=0.6,β=0.1,q=0.1,m=4,Sc=20. 其中参数取值为:u=10,d1=0.2,d2=0.6,β=0.1,q=0.1,m=4,Sc=8. 其中参数取值为:u=10,d1=0.2,d2=0.6,β=0.1,q=0.1,m=8,Sc=13. 提出了一类 Filippov 戒烟模型来研究媒体和政府干预对戒烟的影响.分析了模型的全局动力学性质,得到了各类平衡点的全局渐近稳定的动力学性质.当R1<1时, 平衡点E0是全局渐近稳定的,表明吸烟人数将随着时间推进而趋于0.当R1>1时, 干预强度m与S2成反比, 即当干预强度m越大,S2越小.当S2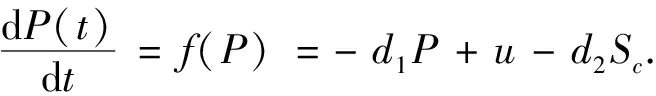
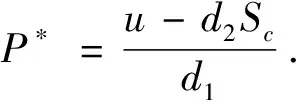
2.5 闭轨的排除
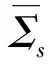
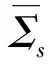
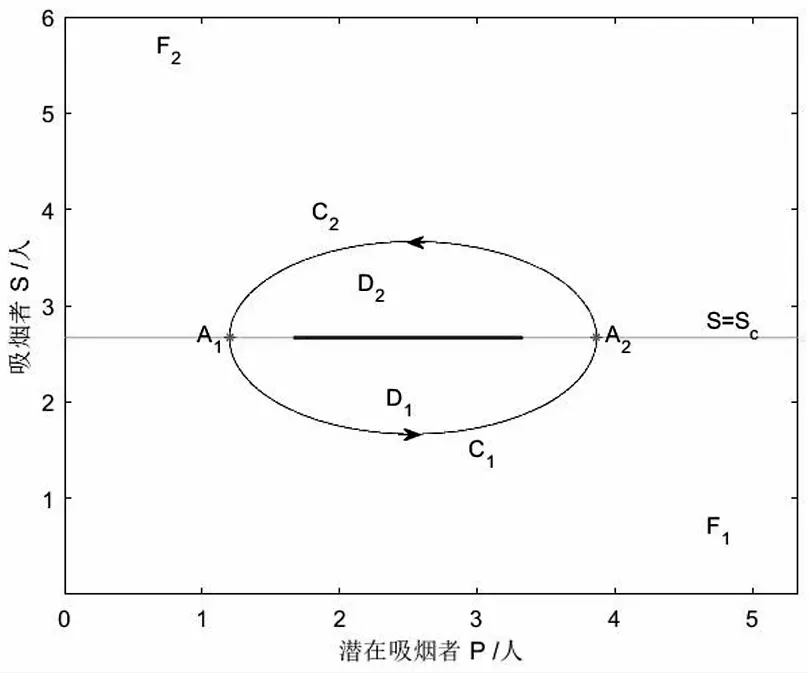

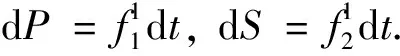

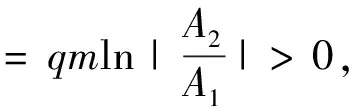
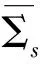
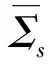
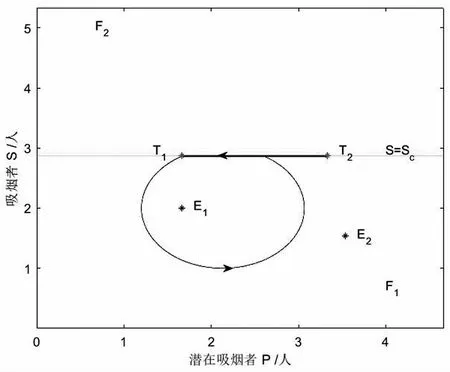
3 全局动力学分析


4 结 论

