基于异质参与者的最优歧视性竞赛规则研究*

王春雷，潘佳玉

(广西大学 商学院，广西 南宁 530004)

1 引 言

在市场经济中，许多资源的配置结果是通过价格实现的，例如股票、古董、土地使用权、与股神巴菲特共进午餐等.但是，还有许多资源的配置并不是通过市场价格机制而是通过竞赛方式完成，例如考大学、找工作、器官移植等.这种竞赛可以概括为:竞赛参与者为获得奖励彼此竞争, 并付出不可收回的努力的过程[1].竞赛是经济社会中的一种普遍现象，在激励和资源配置方面发挥了重要作用.例如，高考考生努力学习以便进入好的大学或者好的专业；研究人员努力发表论文和撰写课题申请书达到职称晋升或获得科研经费支持；运动员努力训练希望在比赛中获得更好的名次.在某些竞赛情形下，竞赛组织者可以通过制定竞赛规则，使得竞赛规则有利于一部分参与者.比如，特定地区或者特殊背景的高考考生可以获得加分；国家或教育部的基金项目管理部门在评审时会向西部地区高校倾斜.

现有关于竞赛理论的研究文献已经对这种歧视性竞赛规则进行了比较深入的研究.Fu(2006)采用全支付拍卖模型论证了大学为保证其学术质量，招生规则一般会偏向于少数族裔[2].Tsoulouhas等(2007)分析了企业在选择首席执行官时，当内部员工比外部人员优秀或者差不多时，规则应有利于内部员工，只有当外部人员相对优秀很多时，规则才应偏向于外部人员[3].Fain(2009)发现在一些情形下歧视性的竞赛规则能够促使所有类型的竞赛参与者都提高努力水平[4].董志强(2009)分析了组织中扶弱抑强的歧视性资源配置现象，发现若互相竞争的代理人能力不对称，扶弱抑强的歧视性资源配置政策将更有利于委托人[5].海江涛等(2013)表明政府在激励投标商参与公共产品技术创新时，如果存在技术外溢，政府应采取偏袒性的竞赛规则[6].侯琨等(2014)论证了如果针对不同类型的竞赛参与者设置不同的约束条件，能够诱致更高的总努力水平[7].

尽管上述研究对理解现实中的竞赛规则设计具有指导价值，但这些模型的假设和结论并不总是令人信服.研究文献通常假设模型只有两位竞赛参与者，按照能力或者对奖品的估值分成高、低两类，但现实中的竞赛参与者通常要多于两位，而且参与人的类别往往要多于两类.更重要的是，在只有两位竞赛参与者时，歧视性竞赛规则通常使得竞赛参与者获胜概率相等[8].也就是说，竞赛的结果看起来是竞赛设计者“丢硬币”决定的.在实际中，尽管竞赛组织者会偏向于能力相对较弱的竞赛参与者，但通常不会使得其获胜概率与能力较强的竞赛参与者一样大.因此，本文放松了竞赛参与者数量的限制，来分析竞赛参与者规模对竞赛结果以及竞赛规则设计的影响.结果表明，即便竞赛参与者只有两类，而且每类参与者人数相等，这种竞赛的均衡结果以及规则设计也与两人竞赛模型有显著差异.此外，研究文献一般基于Lazear和Rosen(1981)[9]提出的锦标赛模型来分析歧视性竞赛规则，但这种模型很难处理参与者数量大于2的情况，因此本文采用的是Tullock(1980)[10]提出的寻租竞赛模型，这一模型已经在皮建才(2012)[11]、魏光兴(2016)[12]等国内文献中得到了运用，不过这些文献分析的仍然是参与者数量为2的情况.

与本文分析框架最接近的文献是Frank等(2013)[13]，他们同样采用寻租竞赛模型分析在多个异质参与者存在的条件下，如何设计歧视性的竞赛规则最大化竞赛参与者的总体努力水平.然而，在他们的模型中，竞赛参与者的努力成本函数是线性的，这会导致歧视性竞赛规则将一部分参与者排除在外.这一结论与现实也不太相符，例如国家自然科学基金委不会因为笔者研究水平太低而不让其申请科研项目.因此，本文假定竞赛参与者的努力成本函数是二次型的，在很多现实情形下，二次型成本函数是一个更好的假设.例如，员工努力工作的时间越长，其负效用也越来越大.在这一假定之下，无论竞赛参与者的能力有多差，竞赛组织者在设计竞赛规则时也不会将他排除在外.

2 基本模型

假设一个竞赛有n个参与者，参与者i付出的努力水平为xi，xi≥0.参与者i获胜的概率表示为：

(1)

如果竞赛奖品可以拆分，如引言中提到的销售竞赛中的奖金，这笔奖金可以分给多位参与竞赛的销售人员，而且参与者的努力结果也可以被观测到，如销售产品的数量，式(1)还可以看作参与者i分享奖金的比例.上述竞赛模型还可以同锦标赛模型联系起来.在最简单的锦标赛模型框架下，竞赛参与者的努力结果用xi+εi衡量，获胜的概率为pi=P(xi+εi>xj+εj,∀j≠i).Jia(2008)[14]用xiεi而不是xi+εi来衡量努力结果，在对误差项εi的分布进行特殊设定的情况下，同样可以得到式(1).

(2)

其中Vi是参与人对奖品的估值.由于竞赛参与者努力水平选择{xi}仅与{ci/Vi}有关，因此在下文中为简便化处理，令所有竞赛参与者对奖品的估值Vi=1，i=1,…,N.此时，ci可以看作是根据奖品估值标准化后的边际成本系数.

竞赛组织者的目标是使得竞赛参与者付出的总体努力水平之和最大，即

(3)

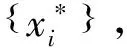
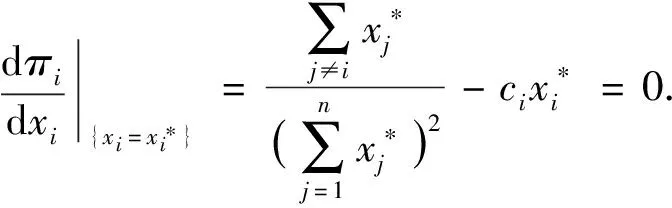
(4)

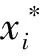
借鉴Cornes和Hartley(2005)[15]的思想，本文提出一种非常简便的均衡求解方法.令

每位参与者付出的努力水平满足条件：

(5)

式(5)的函数形式要比最优反应函数简单得多.均衡时，每位参与者付出的努力水平仅仅与均衡总体努力水平相关.

根据式(5)，均衡时竞赛参与者i获胜的概率为

(6)

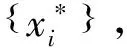
根据以上分析，得到命题1.

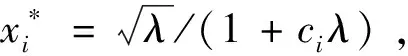
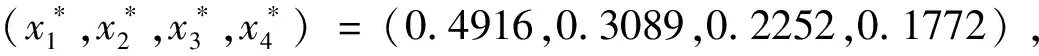
3 歧视性竞赛规则

假设竞赛组织者可以针对每位参与者付出的努力水平设置一个权重wi>0，参与者i获胜的概率变为：

(7)

如果所有的权重相等，表明竞赛规则对所有参与人来说都是公平的.如果权重不相等，表明竞赛规则会对某些竞赛者有利，是一种歧视性的竞赛.在其他人权重不变的条件下，wi越大，竞赛规则越偏向于参与者i.

令yi=wixi，yi衡量的是参与者i在竞赛中的表现，这个指标越大，说明参与者表现越好，其获胜概率也越大.竞赛参与者i的期望收益可以表示为竞赛表现yi的函数，即

(8)

给定权重{wi}的条件下，竞赛参与者i一旦确定努力水平xi，其在竞赛中的表现yi就随之确定，也就是说，xi与yi是一一对应的关系.因此，在竞赛组织者确定歧视性竞赛规则并告知所有竞赛参与者的前提下，参与者i选择努力水平xi最大化其期望收益等同于选择竞赛表现yi最大化其期望收益.

(9)

(10)

根据式(10)，每位竞赛参与者的竞赛表现与总体表现水平之间的关系为

(11)

易知，均衡时竞赛参与者i获胜的概率为

(12)

竞赛组织者的目标是设计权重{wi}使得参与者付出的总体努力水平之和最大，即

(13)

竞赛参与者付出的努力水平xi=yi/wi，而竞赛表现由式(12)确定，因此式(13)可以写成：

(14)

(15)

令拉格朗日函数为

(16)

一阶条件为：

(17)

(18)

(19)

根据式(19)可知，在均衡时，竞赛设计者赋予每个参与者的权重与其边际成本系数成正比.也就是说，最优歧视性竞赛规则设计表现出一种“抑强扶弱”(董志强, 2009)[5]的特征.

根据上述分析，得到命题2.

4 结 论

采用Tullock(1980)提出的寻租竞赛模型，本文分析在有多个异质参与者竞争且每位参与者面临的成本函数为二次型的情况下，如何设计歧视性的竞赛规则使得竞赛参与者的总体努力水平达到最大.研究文献通常利用最优反应函数求解均衡策略以及最优竞赛规则，但很难处理竞赛参与者数量众多的情况, 因为通常需要求解一个多元非线性方程组.本文借鉴Cornes and Hartley(2005)的思路提出了一种非常简便的均衡求解方法.无论竞赛参与者数量有多大，命题1和命题2表明均可以方便地利用一个一元方程求解均衡策略和最优歧视性竞赛规则，即使不能得到解析解，也可以通过数值方法得到均衡结果.此外，竞赛参与者规模对均衡结果以及最优歧视性竞赛规则具有显著影响，即使竞赛参与者只有两类，且每类参与者人数相等，也不能直接简化成两位竞赛模型，因此许多研究文献只考虑两位竞赛参与者的简化设定并不妥当.