常数轮理性秘密分享机制

高先锋，王伊蕾

1.鲁东大学 现代教育技术部，山东 烟台 264025

2.鲁东大学 信息与电气工程学院，山东 烟台 264025

常数轮理性秘密分享机制

高先锋1，王伊蕾2

1.鲁东大学 现代教育技术部，山东 烟台 264025

2.鲁东大学 信息与电气工程学院，山东 烟台 264025

1 引言

秘密分享机制是多方安全计算协议的基础，它是由Blakley和Shamir在1979年分别提出的。经典的(m，n)秘密分享机制的参与者包括一个秘密分发者，记为Dealer和n个参与者，记为(P1，P2，…，Pn)。Dealer试图在n个参与者之间分享秘密s，他首先将秘密分为n个秘密份额，然后将这些秘密份额告诉每个参与者。这n个参与者执行秘密恢复协议，满足一定的条件即可恢复秘密。秘密分享机制满足以下两个条件：（1）参与者获得大于m≤n份（m称为秘密分享的门限值）秘密份额，能够恢复秘密；（2）获得少于m份秘密份额的参与者恢复秘密的任何信息。

Shamir的秘密分享机制是应用比较广泛的一种，其工作原理在于一个m-1阶多项式可以通过m个多项式上的点恢复。假设一个秘密s取自有限域F，其中||F＞n。秘密分发者随机选择一个m-1阶的函数f(x)，使得f(0)=s，(s≠0)，然后把秘密份额f(i)给每一个参与者Pi，其中i=1，2，…，n。参与者接收到他们的份额后，运行一个秘密恢复协议，从而可以恢复秘密值s。

传统的秘密分享机制包括两种参与者：诚实参与者（Honest player）和恶意参与者（Malicious player）。诚实参与者总是遵守协议，而恶意参与者可以采取任意的行为。Halpern和Teague[1]首次提出了理性参与者的概念，所谓理性参与者既不是完全诚实的也不是任意恶意的，而是根据事先设定的收益函数采取行动，他们的目标是如何最大化自己的收益。在文献[1]中，Halpern和Teague假设所有的参与者都是理性的，他们的收益函数需要满足两个条件：（1）参与者希望得到秘密s；（2）在自己得到秘密的基础上，获得秘密的参与者越少越好。

本文将秘密分享看做是一个常数轮重复博弈，在给定收益函数的基础上，为参与者设定了不同的类型，给出了在不完全信息下常数轮RRSSS协议，并证明了其有效性。

2 相关工作

Halpern和Teague的研究表明因为纯策略不是重复弱劣删除策略（Iterated Deletion of Weakly Dominated Strategies，IDOWDS），因此他们提出了一种基于混合策略的理性秘密分享机制。而且，他们认为不存在两个参与者之间的理性秘密分享机制。Gordon和Katz[2]放松了一些条件，使得秘密分发者以概率β在有限域F中选取一个秘密s∈S，以概率1-β选取一个任意元素（假秘密）ˆ，满足，从而可以有效地克服文献[1]中的问题。Shareef[3]提出了一个基于点对点通信信道的理性秘密分享机制，不仅如此，该机制能够抵抗多个任意长参与者（long player）或短参与者（short player）的合谋。但是不能抵制一个长参与者和一个短参与者的合谋。张志芳和刘木兰提出了一个（2，2）理性秘密分享机制，该机制能够实现标准通信模型下的无条件安全[4]。

Maleka和Shareef[5]首先将重复博弈引入理性秘密分享机制中，他们提供了一个异步通信模型下的理性秘密分享机制。基本思想是在重复博弈中引入惩罚策略，使得参与者因为担心未来的惩罚，而在每一轮都采取合作策略。结论包括：（1）对于无限重复博弈或者有限重复博弈（参与者不知道最终轮），存在一个理性秘密分享机制，使得参与者能够恢复秘密；（2）对于有限重复博弈（参与者知道最终轮），不存在理性秘密分享机制，使得参与者可以恢复秘密。然而，有时惩罚策略可能会变成“空洞威胁”，张志芳和刘木兰将（2，2）理性秘密分享机制看做一个不完美信息的扩展博弈，从而可以有效地消除空洞威胁[6]。张恩和蔡永泉提出了一种新型的理性秘密分享机制[7]，其中每一个参与者都不知道当前轮是否为一个测试轮，这与文献[5]中有限重复博弈（参与者不知道最终轮）的情况类似，因此也存在一个有效的理性秘密分享机制。另外，该机制还可以实现公平性和抗合谋的纳什均衡（resilient equilibrium）。在理性秘密分享机制中，除了理性参与者，参与者还可能是恶意的，而且恶意的参与者可能会具有无限的计算能力。另外，在构造理性秘密分享机制时，不仅需要考虑同步通信下的模型，还需要考虑异步通信下的模型。针对这些不同的情况，Gidney[8]提出了四个协议，分别考虑了上述的几种情形，实现了有恶意参与者下的安全性和抗合谋性。

3 基本概念

对于理性参与者，首先要定义他们的效用函数，因为理性参与者所采取的行为完全依赖于能否最大化他们的收益。

3.1 效用和纳什均衡

令μi(ο)代表博弈结果为ο时参与者Pi的效用，δi(ο)=1表示参与者Pi得到秘密，δi(ο)=0表示参与者Pi没有得到秘密。令表示获得秘密的参与者个数。根据文献[2]，效用函数的定义符合以下假设：

（1）对于两个博弈结果ο和ο′，如果满足δi(ο)＞δi(ο′)，则有μi(ο)＞μi(ο′)；

（2）对于两个博弈结果ο和ο′，如果满足δi(ο)=δi(ο′)，且num(ο)＜num(ο′)，则有μi(ο)＞μi(ο′)。

第一个假设说明参与者希望得到秘密，即得到秘密的效用大于没有得到秘密的效用。第二个假设说明，如果两个博弈结果相同，那么参与者希望得到秘密的参与者越少越好。

为简便起见，本文定义了输出结果为ο时，参与者Pi的效用函数（其中i，j=1，2，…，n，且i≠j）：

（1）μi(ο)=U+，如果Pi得到秘密，而Pj没有得到秘密；

（2）μi(ο)=U，如果Pi和Pj都得到秘密；

（3）μi(ο)=U-，如果Pi和Pj都没有得到秘密；

（4）μi(ο)=U--，如果Pj得到秘密，而Pi没有得到秘密。

为了保证参与者有参与理性秘密分享机制的动机，规定：U+＞U＞U-＞U--。

在每一轮博弈，每个参与者都会采取一个策略，所有参与者的策略组合表示为一个策略向量σ=(σ1，…，σi-1，σi，σi+1，…，σn)，其中σi表示参与者Pi的策略（注意σi表示参与者采取的混合策略），σ-i=(σ1，…，σi-1，σi+1，…，σn)表示除Pi以外其他参与者的策略向量表示参与者Pi采取策略，而其他参与者遵守策略组合σ-i。下面给出纳什均衡的概念。

定义1（纳什均衡）一个策略向量σ引入一个纳什均衡，如果对于任何一个参与Pi和任何策略，都有：

纳什均衡能够保证每个参与者没有偏离均衡策略的动机。

3.2 重复博弈

在重复博弈中[9]，参与者多次参加阶段博弈，记为(Γ1，Γ2，…，ΓT)，其中T表示博弈的轮数，它可以是无限值（对应无限重复博弈），也可以是有限值（对应有限重复博弈）。历史H用来记录每一阶段博弈参与者所采取的行动。为了能够记录每一阶段参与者的行动，令表示在第k轮参与者采取的行动，其中表示参与者Pi在第k轮采取的纯策略，a∈A，A表示参与者的所有策略集合。为简便起见，历史从第0轮开始且此时H=Φ，其中Φ表示空集。参与者根据历史hk=(a0，a1，…，ak)决定他当前轮的行动。在每一轮，参与者Pi获得一个效用ui(i=1，2，…，n)。在有限重复博弈中，参与者的总收益是每个阶段收益的和。

4 常数轮RRSSS

在常数轮RRSSS中，参与者知道哪一轮是最后一轮，因此在最后一轮，所有参与者都会采取不合作策略，因为下一轮博弈将结束，即使采取不合作的策略也不会担心将来受到惩罚。根据逆向归纳法，可以推导出在所有轮，参与者都没有合作的动机。然而文献[10]和文献[11]的结论表明，如果放松某些条件，在有限重复博弈中，合作是可以出现的。本文将他们的结论引入到有限重复理性秘密分享机制中，构造了常数轮的RRSSS机制。首先介绍常数轮RRSSS机制中用到的策略。

4.1 常数轮RRSSS的策略

Maleka和Shareef[5]认为在参与者知道最后一轮时，不存在有限RRSSS。他们假设每次分享秘密的参与者都来自于一个相同的集合，如果放松这个条件，允许有不同的参与者执行秘密恢复协议，就可以实现有限RRSSS。参与者根据参加协议的次数，分为长期参与者和短期参与者。如果参与者每次都参与协议，那么就称之为长期参与者，若参与者仅参加一次协议，则称之为短期参与者。一个参与者是长期参与者还是短期参与者取决于他们参加协议的次数。

这里的长期参与者和短期参与者与文献[3]的不同，在文献[3]中，长参与者表示参与者拥有长的秘密份额，而短参与者拥有短的秘密份额。假设在每一轮中只有一个长期参与者，他会一直参与所有轮的RRSSS，而剩余的n-1个参与者是短期参与者，他们只参加一次RRSSS。为了分析方便，将整个参与秘密恢复协议的短期参与者看做一个集合，称之为短期集合。

为了达到相互合作的均衡，短期集合必须在每一轮中先采取行动，否则短期参与者肯定会在每一轮采取不合作策略。这是因为短期参与者只参加一轮秘密恢复协议后就退出，因此不必担心下一轮受到惩罚。如果短期参与者先行，那么为了获得秘密，短期参与者肯定会采取合作的策略。另一方面，长期参与者不能采取纯策略，如果他每次都采取合作策略，那么一旦短期参与者知道了他的策略，那么短期参与者就失去了合作的动机；如果他每次都采取不合作策略，那么一旦短期参与者知道了这一纯策略，短期参与者也不会合作。这是因为，即使短期参与者合作，没有长期参与者的份额，他也无法恢复秘密。因此对于长期参与者来说，他最好采取混合策略。所以在异步通信信道中，每一轮短期参与者先行，长期参与者以概率β采取针锋相对策略（Tit-For-Tat，TFT）。所谓针锋相对策略就是参与者在博弈的第一轮采取合作策略，然后在接下来的每一轮，都将采取对手上一轮的策略。结果表明，在满足一定条件下，长期参与者和短期参与者都可以获得秘密，因为他们在每一轮都采取合作策略。

4.2 常数轮RRSSS机制

当重复博弈是完全信息时，即使参与者有不同的类型，也不存在实际可行的RRSSS，使得参与者获得秘密。这是因为每一个参与者都清楚地知道对手的类型以及他们将采取的策略。然而，在不完全信息下，因为参与者不知道对手的类型，为了能够获得秘密，参与者有互相合作的可能。

为了使参与者在每一轮都采取合作策略，分享他们的秘密份额，最终恢复秘密，本文考虑了不完全信息下的常数轮RRSSS。常数轮RRSSS机制包括两个子协议，秘密分发协议和秘密恢复协议。

秘密分发协议（The dealer’s protocol）：

（1）秘密分发者随机选择一个m-1阶的函数f(x)，使得f(0)=s(s≠0)。

（2）秘密分发者确定一个长期参与者（不失一般性，记为P1）和n-1短期参与者（记为P2，P3，…，Pn）。在不完全信息下，每个参与者知道自己的类型，但是不知道对手的类型。

（3）秘密分发者把秘密份额f(i)给每一个参与者Pi，其中i=1，2，…，n。

秘密恢复协议（The players’protocol）：

（1）每一个参与者在得到秘密份额f(i)后，随机选择一个T-m*-1阶的函数gi(x)，其中gi(0)=f(i)，i=1，2，…，n。T是一个常数，它表示协议执行的轮数，m*表示剩余的轮数，它的值由定理1给出。

（2）在每一轮，包括两个参与者：长期参与者P1和一个短期参与者Pj，j=2，3，…，n。

①短期参与者Pj首先采取合作的策略，将f(j)的子秘密份额gj(1)发送给长期参与者P1。

②长期参与者P1采取混和策略（混合策略以概率β采取TFT策略，以概率1-β采取占优策略。其中TFT策略指的是参与者在第一轮采取合作策略，在以后的每一轮都采取对方上一轮所采取的策略。占优策略指的是，参与者在每一轮都采取不合作的策略）决定是否将f(1)子份额g1(j)发给短期参与者Pj。

（3）协议进行到最后一轮，每个参与者根据自己的子份额，通过朗格朗日插值公式恢复出秘密份额，进一步恢复秘密s。

4.3 机制有效性证明

如果满足一定条件，新机制可以实现RRSSS，并且具有高效性。

引理1存在一个ˉ满足（β表示长期参与者采取针锋相对策略的概率），使得短期参与者在不完全信息下的常数轮RRSSS中，有采取合作策略的动机。

证明短期参与者在每一轮先行，他们不知道长期参与者是否会采取TFT策略。假设长期参与者以概率β采取TFT策略，以概率1-β采取占优策略。

在第k轮，如果短期参与者采取不合作策略，那么长期参与者也采取不合作策略。这是因为如果长期参与者采取TFT策略，那么长期参与者应该选择不合作策略，如果长期参与者选择占优策略，那么长期参与者也应该选择不合作策略，此时短期参与者的收益为U-。

在第k轮，如果短期参与者采取合作策略，那么就有两种情况：

（1）如果长期参与者以概率β采取TFT策略，那么长期参与者应该采取合作策略，此时短期参与者的收益为U。

（2）如果长期参与者以概率1-β采取占优策略，那么长期参与者应该采取不合作策略，此时短期参与者的收益为U--。

在这种情况下，短期参与者的期望收益为βU+(1-β)U--。作为理性参与者，短期参与者必定采取收益大的策略。

为了促进短期参与者采取合作策略，需要使短期参与者采取合作策略的效用大于采取不合作策略的效用。因此，需要满足：

证明证明的主要思路是：对于n个理性参与者，共进行T轮阶段博弈，那么秘密分发者选择门限m时，需要满足m≤T-m*。如果在T-m*轮之前，所有的参与者都采取合作策略，那么每个参与者就可以获得足够的子秘密份额恢复秘密份额，进而恢复秘密。

令m*表示剩余的轮数，根据引理1，已知短期参与者有采取合作策略的动机。不失一般性，假设在第T-m*轮前，短期参与者不分享份额，那么长期参与者也不分享份额（引理1），短期参与者在第T-m*轮采取合作的策略。在接下来的m*轮，短期参与者和长期参与者都采取不合作策略，他们的收益均为U-。本文不考虑这种情形，因为这对双方都不利。

假设短期参与者合作（在不完全信息下，根据引理1，短期参与者肯定会合作），如果长期参与者也采取合作策略，那么他在这一轮得到收益U。在接下来的m*-1轮，新进入协议的短期参与者如果观察到上一轮的结果是双方都合作，那么新加入的短期参与者认为长期参与者在这一轮也有合作的倾向，因此短期参与者和长期参与者会一直合作下去。在这种情况下，长期参与者的总收益是(m*-1)U。在接下来的m*-1轮，一旦有一轮长期参与者采取不合作策略（而短期参与者仍然采取合作策略），那么长期参与者在第T-m*的收益为U+。但是在后续轮中，新加入的短期参与者因为害怕得不到秘密而不采取合作策略。因此新加入的短期参与者在剩余的m*-1轮都会采取不合作策略。因为不管长期参与者是什么类型，不合作策略总是短期参与者的占优策略，因此一旦长期参与者采取不合作策略，在后续的m*-1轮，参与者会进入相互不合作状态。在这种情况下，长期参与者的总收益为：U++(m*-1)U-。为了使长期参与者具有合作的动机，必须使长期参与者合作时的收益大于不合作时的收益，需要满足：

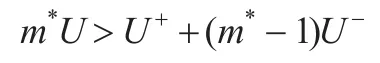
因此有：

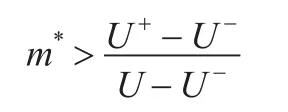
表1对本文方案和其他理性秘密分享方案进行了比较，可以看出，给定满足条件的随机数，本文方案在纳什均衡、期望执行时间和通信信道方面均占有优势。

表1 各种理性秘密分享方案的比较

5 结束语

为了在常数轮RRSSS中能够引入相互合作的策略，为参与者设定了不同的类型，使得参与者在知道最后一轮的常数轮RRSSS中也能都采取合作策略，进而成功恢复秘密。在不完全信息下，构造了一个常数轮RRSSS，可以证明，如果满足一定的条件，参与者可以实现相互的合作，从而达到恢复秘密的目的。

[1]Halpern J，Teague V.Rational secret sharing and multiparty computation：extended abstract[C]//Proceedings of the Thirty Sixth Annual ACM Symposium on Theory of Computing，Chicago，2004：623-632.

[2]Gordon S D，Katz J.Rational secret sharing，revisited[C]//De Prisco R，Yung M.The Fifth Conference on Security and Cryptography for Networks，Maiori，2006：229-241.

[3]Shareef A.Rational secret sharing without broadcast[EB/OL]. [2012-01-05].http：//eprint.iacr.org/2010/249.

[4]Zhang Zhifang，Liu Mulan.Unconditionally secure rational secret sharing in standard communication networks[C]//Information Security and Cryptology，2011，6829：355-369.

[5]Maleka S，Shareef A，Rangan C P.Rational secret sharing with repeated games[C]//ISPEC’08 Proceedings of the 4th International Conference on Information Security Practice and Experience，Heidelberg，2008：334-346.

[6]Zhang Zhifang，Liu Mulan.Rational secret sharing as extensive games[J].Science China Information Sciences，2013，56.

[7]Zhang En，Cai Yongquan.A new rational secret sharing scheme[J]. China Communications，2010，7（4）：18-22.

[8]Gidney.Rational secret sharing with and without synchronous broadcast，conspicuous secrets，malicious players and unbounded opponents[D].MCSc Thesis Defence，2012.

[9]Osborne M，Rubinstein A.A course in game theory[M].Cambridge：MIT Press，2004.

[10]Andreoni J，Miller J H.Rational cooperation in the finitely repeated prisoners’dilemma：experimental evidence[J].The Ecomonic Journal，1993，103（418）：570-585.

[11]Milgrom P，Roberts J.Predation，reputation，and entry deterrence[J].Journal of Economic Theory，1982，27（2）：280-312.

GAO Xianfeng1,WANG Yilei2

1.Department of Modern Education Technology,Ludong University,Yantai,Shandong 264025,China
2.School of Information and Electrical Engineering,Ludong University,Yantai,Shandong 264025,China

Finitely repeated rational secret sharing scheme is first proposed by Maleka and Shareef who conclude that there does not exist a Repeated Rational Secret Sharing Scheme（RRSSS）within constant rounds.However,RRSSS within infinite rounds is lack of efficiency and has no application value.To achieve an efficient RRSSS within constant rounds,players are set different types.An efficient RRSSS within constant rounds is put forward under incomplete information and then its validity is proved. Compared with other rational secret sharing schemes,given proper conditions,the new scheme has advantages in Nash equilibrium, expected running time and communication channel.

game theory;Nash equilibrium;finitely repeated games;rational secret sharing scheme

基于重复博弈的理性秘密分享机制，首先由Maleka和Shareef提出，他们认为不存在常数轮的重复理性秘密分享机制（Repeated Rational Secret Sharing Scheme，RRSSS）。然而，无限轮RRSSS效率低下，不具备应用价值。为了实现高效的常数轮RRSSS，为参与者设置了不同的类型，提出了不完全信息下的常数轮RRSSS机制，并证明了机制的有效性。与其他理性秘密分享方案比较，在给定条件下，新方案在（纳什）均衡、期望执行时间和通信信道方面均具有优势。

博弈论；纳什均衡；重复博弈；理性秘密分享机制

A

TP309.7

10.3778/j.issn.1002-8331.1203-0439

GAO Xianfeng,WANG Yilei.Rational secret sharing scheme with constant rounds.Computer Engineering and Applications,2013,49（18）：65-68.

国家自然科学基金（No.60875039）；山东省自然科学基金（No.ZR2011FM017）。

高先锋（1968—），男，副教授，高级工程师，研究领域为网络安全和秘密分享机制；王伊蕾（1979—），女，博士研究生，讲师，研究领域为多方安全计算和博弈论。E-mail：xianfenggao_ldu@163.com

2012-03-19

2012-06-08

1002-8331（2013）18-0065-04

CNKI出版日期：2012-07-16 http://www.cnki.net/kcms/detail/11.2127.TP.20120716.1500.021.html