基于NGWO 的光伏信息设备的状态预测∗

王靖程 王金明 敖 海 李国庆 姚玲玲 陈 仓

（1.西安热工院研究有限公司 西安 710054）（2.华能金昌光伏发电有限公司 金昌 737199）（3.华能新能源股份有限公司 北京 100036）

1 引言

光伏信息设备的状态预测对光伏系统的正常运转和实时准确监控及管理起到了重要作用。它是指根据信息设备的CPU 使用率、内存使用率、磁盘使用率和温度的历史数据，来推测一段时间后设备的负载状态信息。

目前，对信息设备负载状态的预测方法主要有两大类。一类是基于统计学知识的方法，如时间序列方法［1～3］、回归分析法［4］和灰色模型预测法［5］。但随着许多系统规模的变大，设备状态数据也随之海量增长并且复杂多变，这类方法已经不能保证这种多维非线性不平稳时间序列的预测精度。另一类方法则适用于高维度、非线性时间序列的建模分析，如支持向量机（support vector machine，SVM）［6］、人工神经网络［7］等。SVM 能够找到全局最优解，但操作比较复杂，其参数选取需要一定的先验知识，参数的合适与否决定着预测结果的优劣，致使模型的泛化能力较弱。人工神经网络自适应、自学习能力较强，不需要先验知识，而且由于其实现简单，目前在设备状态预测领域中已得到了广泛的应用。循环神经网络（recurrent neural network，RNN）是一种引入了定向循环的人工神经网络，能够处理那些输入输出之间前后具有关联的问题［8］。

但循环神经网络在处理长时间的时间序列时存在梯度消散的现象［9］，文献［10］提出了长短期记忆（long-term and short-term memory，LSTM）神经网络，该网络是RNN 的一个变种，能够处理循环神经网络梯度消散的问题，在时间序列预测领域取得了很好的成绩［11～14］。但传统的LSTM 是利用随时间反向传播算法（backpropagation through time，BPTT）［15］来确定网络参数的，该算法时间复杂度高且易陷于局部最优。

基于上述分析，本文提出一种用小生境灰狼优化（niche grey wolf optimization，NGWO）算法改进的长短期记忆神经网络预测光伏信息设备状态的方法。实验结果表明，该方法提高了对信息设备状态预测的精度。

2 理论基础

2.1 LSTM神经网络

LSTM作为RNN的一个变种，在RNN模块的基础上引入了记忆单元状态，解决了RNN 存在的问题。LSTM 有三个特殊的门：遗忘门、输入门、以及输出门。LSTM神经网络通过对于这三个门的参数及权重调整，来解决循环神经网络难以处理长时依赖序列的问题。其重复模块的内部结构如图1所示。

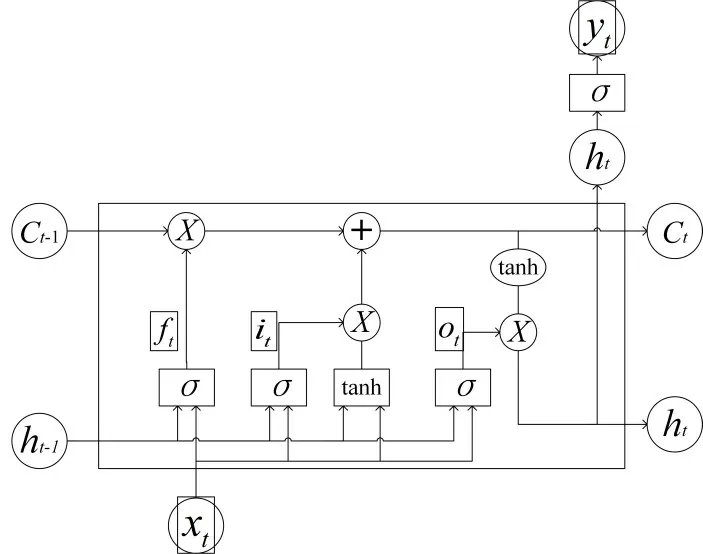
图1 LSTM结构示意图

遗忘门负责选取从单元状态中移除的信息，计算公式为

输入门负责新信息的输入，计算公式为

式（1）～（7）中，t∈{1 ，2，3…l} ，激活函数选取sig⁃mod函数。

根据上述公式计算可求得系统的输出，接着采用随时间反向传播算法，修正网络中的参数并最终确定。LSTM在时间序列预测领域取得了很好的成绩。但其在确定参数的时候采用的是BPTT 算法，该算法时间复杂度较高且容易收敛于局部最优解。

2.2 基本灰狼优化算法

灰狼优化（grey wolf optimization，GWO）算法［16］是一种根据狼群群体智能，基于狼群的社会等级制度和捕食行为而提出的群体智能优化算法。狼群中存在严格的社会等级制度，社会等级层次从上到下依次是α，β，δ和ω共4层，狼群算法建立了一个狼群中的狼和潜在解对应的模型［17］。α狼代表当前位置最好的狼（当前最优解），是捕猎过程中的领导者；其次是β和δ，捕猎过程中他们会协助α狼对狼群进行管理和决策；其他的狼被定义为ω，根据α，β，δ三只狼的位置更新自己的位置。围捕结束后位置最好的狼将对应于我们所寻找的最优解。

相比于粒子群优化算法［18］、蚁群优化算法［19］、遗传算法［20］，灰狼优化算法在函数优化方面有着结构简单、易于操作等优点，但在搜索最优的过程中，因为群体多样性较差，所以会较易进入局部最优的状态。基于上述分析，在灰狼优化算法的基础上，引入小生境技术，提出利用小生境灰狼优化（NG⁃WO）算法来优化LSTM的设备状态预测方法。

3 NGWO-LSTM预测模型

小生境（Niche）是指特定环境下的一种生存环境，在进化过程中，生物总是倾向与自己习性相像的个体一起生活，进而产生后代［21］。在每一代进化前，小生境技术依据个体间的距离将群体分成多个小生境群体，再在不同小群体之间配对产生下一代。利用小生境技术对灰狼优化算法进行优化，首先通过传统GWO 算法算出每个个体的适应度值，给定一个小生境半径，当个体间的距离小于该值时，比较这些个体的适应度值，接着对适应度值较低的个体施加惩罚，以提高搜索全局最优的能力。

小生境灰狼群优化算法具有计算较为简单、能够收敛到全局最优的优点。所以本文利用基于小生境灰狼优化算法的LSTM 模型（NGWO-LSTM）来对光伏系统信息设备的状态参数进行预测，通过NGWO 算法来优化LSTM 的网络参数，将LSTM 对时序数据的强大处理能力与NGWO 算法的高效优化能力相结合，使得能够高效、精确地对设备的状态进行预测。

NGWO-LSTM 模型的网络结构和传统LSTM的网络结构相同，如图2。从LSTM 的相关计算公式可以得到我们需要确定的参数（矩阵）有13 个，分 别 是wfx∈Rhidden×lookback，wfh∈Rhidden×hidden，bf∈Rhidden×1，wix∈Rhidden×lookback，wih∈Rhidden×hidden，bi∈Rhidden×1，wcx∈Rhidden×lookback，wch∈Rhidden×hidden，bc∈Rhidden×1，wox∈Rhidden×lookback，woh∈Rhidden×hidden，bo∈Rhidden×1，wyh∈Rpredstep×hidden。

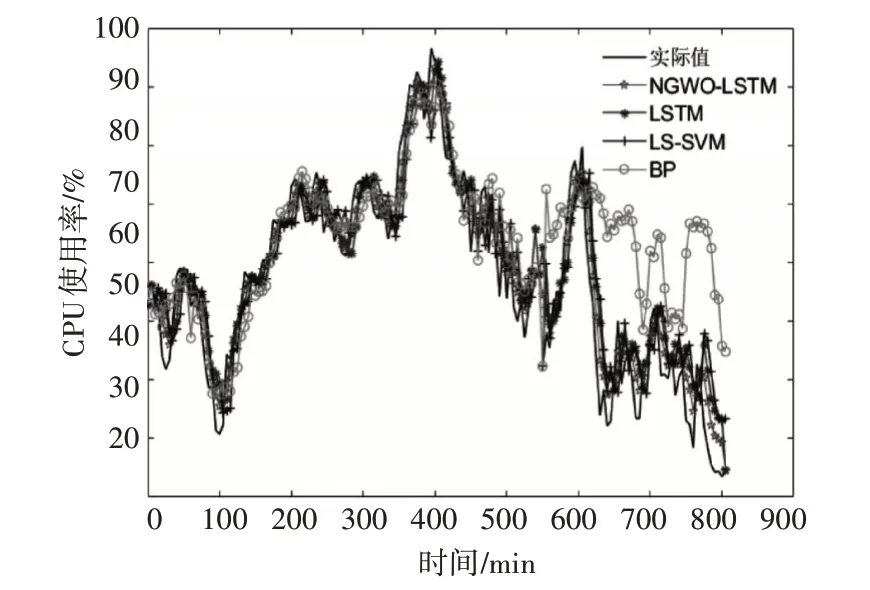
图2 CPU使用率预测的实验结果对比图

其中，hidden为隐藏层单元的个数；lookback为时间步，表示当前的输入与前陆续多少步的输入有直接联系；predstep表示预测未来多少步的输出。

因为NGWO 算法中的每只狼都是一个潜在解，所以每只狼的位置要能表示出这13 个参数（矩阵），故狼的位置的长度为

假设搜索空间是M维的，也即狼的位置的长度为M，那么灰狼i的位置可以用一个矢量来表示Xi=(Xi1，Xi2，…，XiM)T。假设狼群中有N只狼，则整个狼群可表示为X=(X1，X2，…，XN)。

个体间的距离选用欧式距离来衡量，对于M维搜索空间，灰狼i的位置为Xi=(Xi1，Xi2，…XiM)T，灰狼j的位置为Xj=(Xj1，Xj2，…XjM)T，于是灰狼i和灰狼j的距离为

若该距离小于给出的指定参数小生境半径σshare，即dij＜σshare，则将它们纳入到小生境群体。

适应度函数值是评价种群中灰狼个体好坏程度的一个标准，它是基于目标函数构造的，灰狼的适应度值越大，则更有机会作为α狼。

我们的目标是使模型给出的预测值与实际值相比偏差尽可能地小，所以可选取最小化为目标函数。其中为实际值，yt为模型的输出值，T为所预测的时间序列的长度。故NGWO算法的适应度函数可设置为

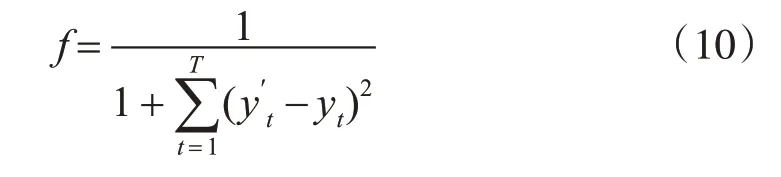
NGWO 算法改进的LSTM 时间序列预测模型步骤如下：

步骤一：确定LSTM 神经网络中hidden、look⁃back 和predstep 的值，并将输入（X）重构为LSTM 预期的3D格式，即［Samples，Timesteps，Features］。

步骤二：确定小生境灰狼优化算法的维度M，群体中的灰狼个体数N、最大迭代次数tmax、小生境半径σshare和惩罚函数penalty。

步骤三：初始化灰狼群体，通过随机方法产生每只灰狼的位置Xi，j～U(lj，uj)(1 ≤i≤N，1 ≤j≤M)，其中U是随机分布函数，lj、uj表示搜索区间的搜索上界和下界。

步骤四：对每个灰狼个体进行下列操作：

1）将每个灰狼个体Xi分解成LSTM的参数；

2）代入样本数据，根据上述参数计算LSTM 神经网络的输出值y；

3）根据式（10）计算灰狼Xi的适应度值fi。

步骤五：比较每个灰狼的适应度值，将适应度值前三的灰狼个体的位置分别记为Xα、Xβ、Xδ，并将适应度值最好的Xα作为LSTM 网络参数的最优解。

步骤六：更新剩余个体ω的位置。在更新灰狼i的位置时，先分别计算出灰狼i和狼α，β，δ之间的距离，距离计算公式如下：

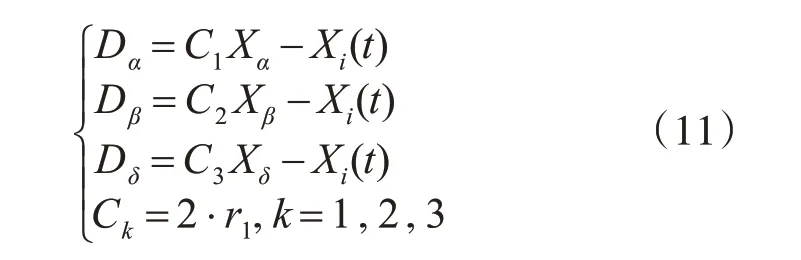
式中，Dα、Dβ、Dδ分别代表灰狼i距狼α，β，δ的距离；Xα、Xβ、Xδ分别表示狼α，β，δ的位置；Xi(t)表示狼i在第t 代的位置；r1为0～1 之间的随机数。

在得到灰狼i距位置最好的三只狼的距离后，狼i就需要向这三只狼移动，以更新自己位置，计算公式如下：

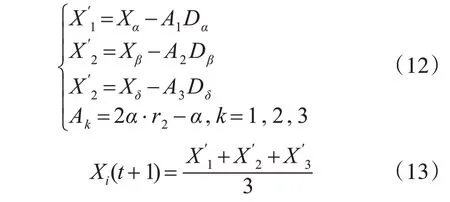
式中，分别是狼i朝α，β，δ狼移动的矢量；Xi(t+1)是更新后的最终位置；r2是［0，1］间的随机数；α是收敛因子，其计算公式为α=2-，t是当前迭代次数，tmax是最大的迭代次数。可以发现，迭代因子α随着迭代次数的增加从2 线性递减到0，所以Ak的绝对值有两种可能：1 ＜ |Ak|≤2 或 |Ak|≤1。若1 ＜ |Ak|≤2，则该狼会远离当前位置较好的狼；若≤1，则会向位置较好的狼靠拢。

步骤七：按照式（9）计算灰狼个体间的距离，当dij＜σshare时，比较灰狼i和灰狼j适应度值的大小，对适应度度值较小的灰狼施加惩罚函数。即若dij＜σshare，min(fi，fj)=penalty（penalty函数的惩罚力度根据所求函数解的大小来决定）。

步骤八：若t大于tmax，则终止算法并输出最优解Xα；否则返回步骤四。

最后获得的Xα即为LSTM 网络参数对应的最优解，之后，便可以将训练好的模型运用于测试。

4 实验及结果分析

为了验证基于小生境灰狼优化（NGWO）算法的长短期记忆（LSTM）神经网络在光伏信息设备状态预测中的精度和泛化能力，本文使用LS-SVM、BP神经网络和原始LSTM 作为参比方法，与本文的NGWO-LSTM预测模型进行比较。

实验采用的数据来自甘肃某光伏电站的信息设备的历史状态数据，其数据记录间隔为5min。在使用各个预测方法进行预测之前，需对数据进行预处理，剔除掉明显的异常点，然后对数据进行归一化处理，并将数据集划分为训练集和测试集。本文选取2017 年10 月1 日至2 日的一共560 组有效采样数据，将前400组数据划分为训练集，将后160组数据划分为测试集。在数据集中，每组数据包括CPU使用率、内存使用率、磁盘使用率和主板温度4个值。

4.1 实验参数设置

NGWO-LSTM 的种群规模N=30，最大迭代次数tmax=400，小生境半径σshare=0.5，LSTM 神经网络的隐藏层层数为1，隐藏层节点数为8，激活函数均使用sigmood 函数。传统LSTM 的网络结构和改进的LSTM 的相同，迭代50次。最小二乘支持向量机LS-SVM 的正则参数γ=3000，平方带宽δ2=1000。BP神经网络的隐藏层数为1，隐藏层节点数为8，最大迭代次数为500，学习率为0.02。采用Matlab 对本文提出的预测方法及对比方法进行仿真实验，衡量预测精度的指标采用绝对平均百分比误差（MAPE）、绝对平均误差（MAE）和均方根误差（RMSE），计算公式如式（14）～（16）所示。

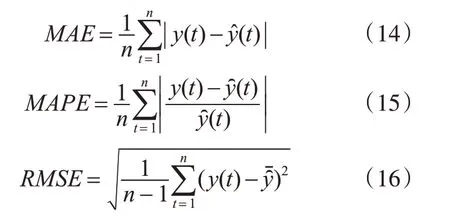
其中，y(t)表示预测的序列值，y̑(t)表示实际序列值。

4.2 实验结果分析

利用Matlab实现各种预测方法，实验结果如表1～4和图3（以CPU使用率为例）所示。

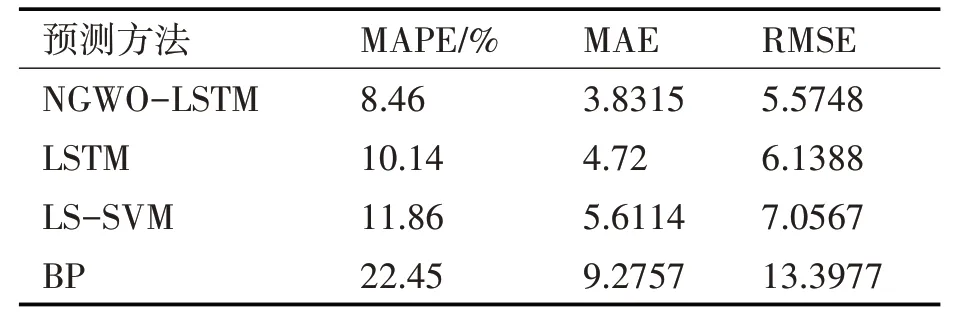
表1 CPU使用率预测实验结果对比

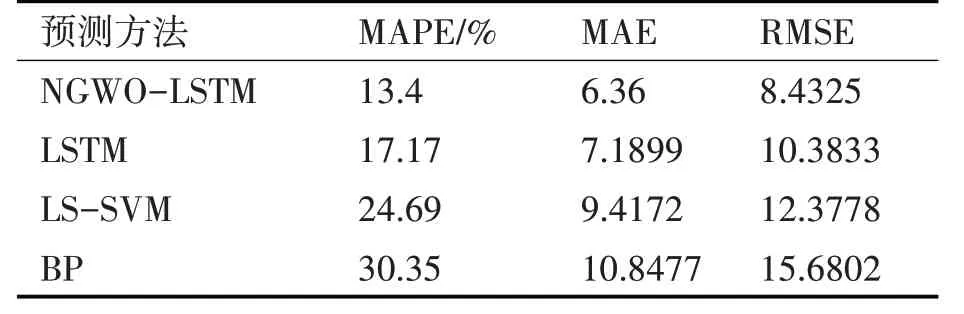
表2 内存使用率预测实验结果对比

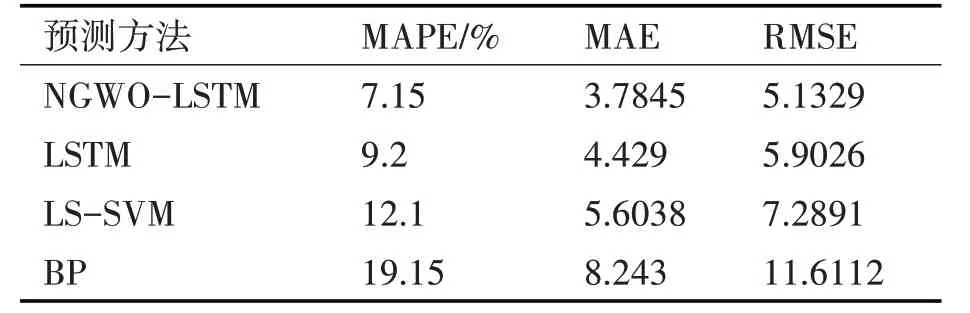
表3 磁盘使用率预测实验结果对比

表4 主板温度实验结果对比

从表1～4 和图3 可以看到，NGWO-LSTM 的预测效果要明显优于其他几种预测方法，其预测值更接近实际值，设备状态的各个属性值预测结果如图4 所示。体现了小生境灰狼算法和长短期记忆神经网络结合的优势，长短期记忆神经网络因其自身结构本身十分适合对前后有关联的时序数据进行处理，小生境灰狼算法则对其网络参数的确定过程进行优化，使其能够快速收敛和寻找全局最优。以CPU 为例进行具体说明，NGWO-LSTM 预测的结果的MAE 相比于传统LSTM、LS-SVM 和BP 神经网络分别降低了0.8885、1.7799 和5.4442，体现出NG⁃WO 算法在优化参数上的优势，减小了算法陷入局部最优的概率，能更好地自适应调整优化LSTM 神经网络的连接权值和阈值。此外，NGWO-LSTM 预测结果的RMSE 也都比其他预测方法的要低，说明该方法泛化能力较强，具有很好的稳定性，波动较小。

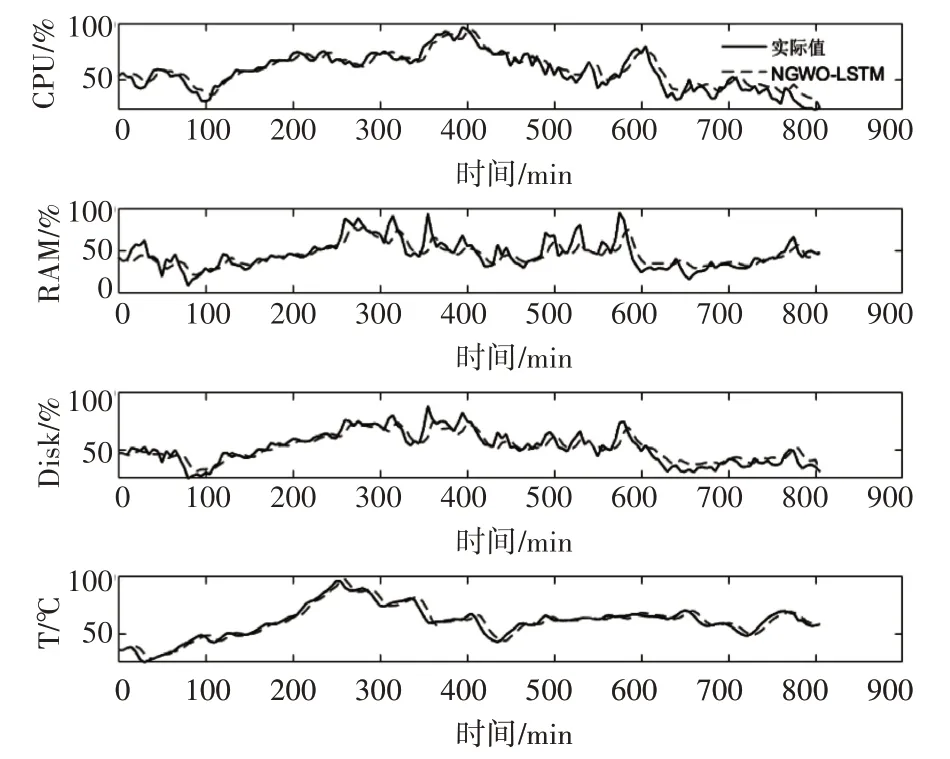
图3 NGWO-LSTM 设备状态预测图

5 结语

本文利用小生境灰狼优化（NGWO）算法优化长短期记忆（LSTM）神经网络来对光伏信息设备状态进行预测。该方法利用小生境灰狼优化算法对LSTM 的网络参数进行优化，将NGWO 算法的快速收敛、全局搜索寻优能力和LSTM 对时间序列数据强大的处理能力相结合，提高了LSTM 对时间序列数据的预测精度。 实验结果表明，该方法能够很好地把握光伏信息设备状态的变化规律，具有较好的预测精度和泛化能力，对设备的状态监控、评估及异常告警具有重要作用。