一种改进的不平衡数据过采样算法BN-SMOTE∗

杨赛华 周从华 蒋跃明 张付全 张 婷

（1.江苏大学计算机科学与通信工程学院 镇江 212013）（2.无锡市第五人民医院 无锡 214073）（3.无锡市妇幼保健院 无锡 214002）（4.无锡市精神卫生中心 无锡 214151）

1 引言

不平衡学习问题包含不同类别之间数据样本的不均衡分布，其中大多数样本属于某种类别，而剩余的样本属于其它类别。许多实际的应用领域中都存在不均衡数据集的分类问题，例如医疗诊断［1］、信息检索系统［2］、欺诈性电话的检测［3］、直升机故障检测［4］等。传统的分类方法倾向于对多数类有较高的识别率，对于少数类的识别率却很低。因此不均衡数据集的分类问题的研究需要寻求新的分类方法和判别准则。

目前最流行的处理不平衡学习问题的方法多是基于过采样方法来延伸的。在本文中，首先介绍了SMOTE 算法以及它的一种改进方案Border⁃line—SMOTE 算法，同时指出在某些情况下，Bor⁃derline—SMOTE 算法无法正确识别出所有的边界样本。基于这一问题，我们提出一种新的过采样方法Borderline Neighbor Synthetic Minority Oversam⁃pling Technical（BN-SMOTE），其目标是构建出一个难以学习的边界少数类样本集，再从中选择少数类样本参与到样本合成中。基本思想是：1）对原始少数类样本进行过滤操作去除噪声；2）构建难以学习的边界少数类样本集；3）合成新的少数类样本。

2 相关工作

2.1 相关算法研究

近些年关于不平衡数据分类的研究已经引起了广泛的关注。He 和Garcia［5］将这些不同的不平衡数据研究方法主要分成了以下四类：采样方法；代价敏感学习方法；基于核的方法与主动学习方法以及如单分类算法、新奇检测等方法。本文将对目前已经提出的一些经典过采样方法作简单介绍。

最简单的方法是随机过采样算法，其中合成的少数类样本都是随机重复的，但是这样容易产生模型过拟合的问题［6］。过采样中另一种主要的方法是根据数据合成样本，其中最著名的算法就是SMOTE［7］。SMOTE 的基本思想是对少数类样本进行分析，并根据少数类样本人工合成新的样本添加到数据集中。

为了提高SMOTE 算法的性能，目前已经提出了很多对于SMOTE 的延伸算法。Han［8］等提出一种命名为Borderline-SMOTE 的过采样算法。Bor⁃derline-SMOTE算法最主要的目的是寻找在边界区域类的少数类样本，在这个方法中只使用这些边界区域内的少数类样本来合成新样本，因为这些少数类样本是最容易被误分类的样本。

Sáez等［9］提出了一种名为SMOTE-IPF的框架，在这个框架中，首先利用SMOTE 算法对少数类样本进行过采样处理，之后通过迭代分割滤波器［IPF］方法对存在的噪声数据进行滤波操作，通过一系列的数值实验，结果表明这个框架具有很好的效率。过采样方法可能会对分类器产生额外的偏差，这会降低分类器在大多数类样本上的性能。为了防止这种劣化，S. Chen 等［10］将过采样和bost⁃ing 相结合，提出一种RAMOBoost 算法来有效地学习不平衡数据。H.Guo［11］等也提出DataBoost IM 方法，通过bosting和数据生成来学习不平衡数据。

2.2 Borderline—SMOTE算法

原始的SMOTE 算法对所有的少数类样本都是一视同仁的，但在实际建模过程中，我们发现那些处于边界位置的样本更容易被错分，因此利用边界位置的样本信息产生新样本可以给模型带来更大的提升。Borderline-SMOTE 便是在SMOTE 方法的基础上进行了改进，只对少数类的边界样本进行过采样，从而改善样本的类别分布。具体步骤描述如下。

假设原始样本集为T，其少数类样本集P，多数类为N。P={p1，p2，…pi，…，ppnum}，N={n1，n2，…ni，…，nnnum}，其中ppnum，nnnum分别表示少数类样本个数和多数类样本个数。

1）计算少数类样本中的每个样本点pi与所有训练样本的欧氏距离，获得该样本点的m近邻（m值为用户设定）。

2）对少数类样本进行划分。设在m近邻中有m'个多数类样本点，显然0 ≪m'≪m。若m'=m，即m近邻均为多数类样本，pi则被认为是噪声；若0 ≪m'≪m2 ，则pi被 划 分 为 安 全 样 本；m2 ≪m'＜m，则pi被划分为边界样本。将边界样本 记 为 {，…，} ， 其 中 0≪dnum≪pnum，其中dnum为少数类样本中边界样本的个数。

3）计算边界样本点pi' 与少数类样本P的k近邻，根据采样倍率N，选择s个k近邻点与进行线性插值，合成少数类样本：

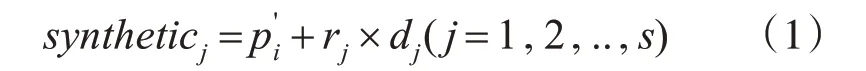
其中rj是介于0 与1 之间的随机数；dj表示样本点与其s个近邻的距离。

4）将新合成的少数类样本与原始训练样本T合并，构成新的训练样本T'。

与SMOTE 方法相比，Borderline-SMOTE 方法只针对边界样本进行近邻线性插值，使得合成后的少数类样本分布更为合理。 但是Border⁃line-SMOTE 算法仍存在许多缺陷，其中一个问题就是无法有效地分辨出噪声样本。在这个算法中，只有当最近邻所有样本都为多数类时，少数类才会被判断为噪声。然而当只有两个少数类样本被大多数类包围时，依然会认为这两个少数类样本处于边界区域，但是显然它们是属于噪声的。

另一个主要问题则是在某些情况下，上述判定方法并不能找到边界位置的少数类样本点［12］。如图1 所示，其中五角星代表多数类样本，圆圈代表少数类样本。从图中我们可以看出，A、B点为离决策边界最近的少数类样本点，用这两个点进行样本生成能够得到好的新样本。假设m=5，可以发现少数类样本点A与B的最近m近邻样本中，均为少数类样本点而没有多数类样本，即m'=0。而根据上述判定方式，此时0 ≪m'≪m2，则A、B 点均被划分为安全样本，这种错分方式将会导致之后的新样本生成过程中，不会使用到A、B两点进行样本生成。由此造成的决策边界附近的少数类样本信息减少，会大大影响模型的性能。

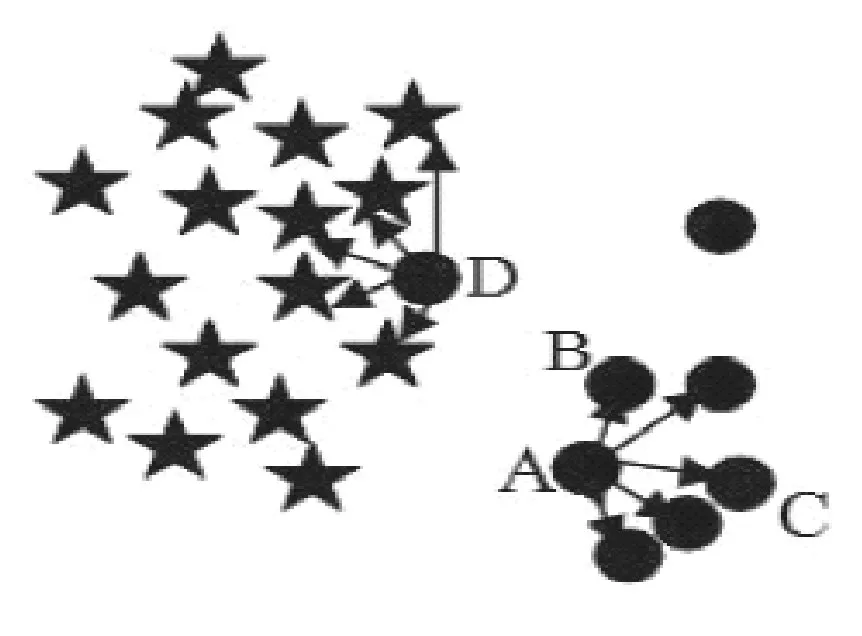
图1 被错分的边界样本少数类样本

3 一种新的算法BN-SMOTE

在新样本的合成过程中，并不是所有的少数类样本都是重要的，因为其中有一部分可能很容易被学习，对于新样本的合成提供的信息少。因此，我们有必要确定一组难以学习的少数类样本，并通过它们合成新的样本。这些样本通常位于决策边界附近，大多数现有的过采样方法［7～8］没有明确地识别难以学习的样本。虽然Borderline-SMOTE 算法试图找到一组边界少数类（难以学习）样本，但我们在上节已经说明了它无法正确识别出所有的边界样本。基于该算法的思想，我们采用一种新方法BN-SMOTE来识别难以学习的少数类样本，并构建成一个少数类样本集。该方法分为两个阶段：在第一阶段，BN-SMOTE从原始少数类样本集Smin中识别出最难学习的少数类样本，并通过所识别出的样本构建一组Simin样本集；第二阶段，BN-SMOTE 从Simin样本集中选择少数类样本来进行新样本的合成，并将合成出的新样本添加到Smin中来生成输出集Somin。主要步骤描述如下：

算法BN-SMOTE（Smax，Smin，N，k1，k2，k3）

输入：

1）Smax：多数类样本集；

2）Smin：少数类样本集；

3）N ：需要生成的新样本数量；

4）k1：用来去除噪声的k近邻值；

5）k2：用来生成少数类集合的多数类集合的数量；

6）k3：用来生成少数类集合的少数类邻居的数量。

程序开始：

1）对于每个少数类样本xi∈Smin，计算其最近邻集合NN(xi)，其中NN(xi)包含了与xi欧式距离相距最近的k1个样本。

2）去除掉那些在其k1 近邻中没有其他少数类存在的少数类样本，组成一个过滤后的少数类样本集Sminf：

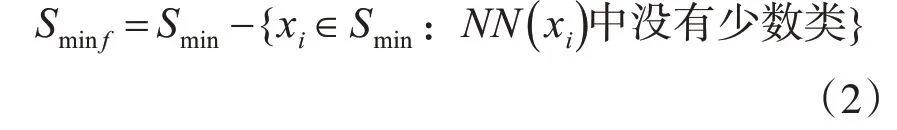
3）对于每个少数类样本xi∈Sminf，计算其最近邻的多数类样本集合Nmaj(xi)，其中Nmaj(xi)包含了与xi欧氏距离最近的k2 个多数类样本。

4）对所有的Nmaj(xi)集合作合并操作得到处于边界区域的多数类样本集合：

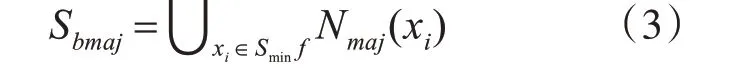
5）对于每个多数类样本yi∈Sbmaj，计算其最近邻的少数类样本集合Nmin(yi)。其中Nmin(yi)包含了与yi欧式距离相距最近的k3 个少数类样本。

6）对所有得到的Nmin(yi)少数类样本

作并集，得到处于边界区域最难学习的少数类样本集Simin：

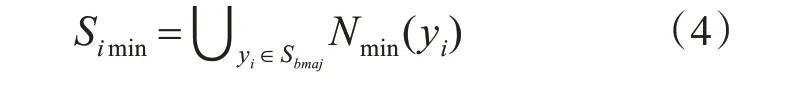
7）初始化集合Somin，使得Somin=Smin。

8）Do forj=1…N。

（1）从少数类样本集合Simin中选择一个样本x，再随机选择另一个样本y；

（2）生成一个新样本s：s=x+α×(y-x)，其中α是处于［0，1］的随机数；

（3）将s放入集合Somin中：Somin=Somin∪{s} 。

9）结束循环。

输出：过采样处理的少数类样本集合Somin。

4 实验

4.1 数据集描述

本文实验数据来自于UCI 机器学习数据库中的3组真实数据集［13］。其中Abalone和Pima数据集是二分类不平衡数据集，Phoneme 是多分类数据集，我们将Phoneme 数据集中的Class’1’作为少数类，其他类共同作为多数类。具体描述如表1所示。

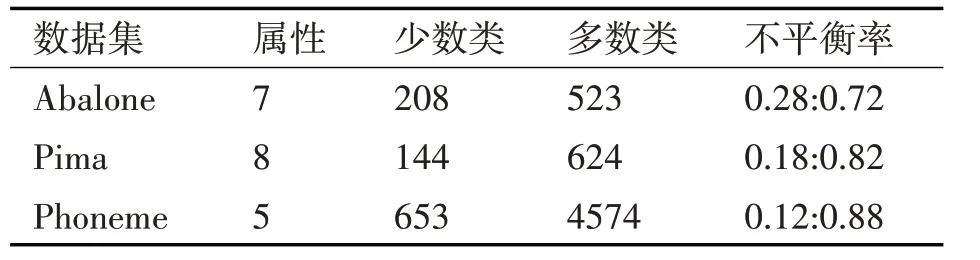
表1 数据集描述

4.2 评价指标

对一个二分问题来说，会出现四种情况，如表2所示。

表2 二分类的混淆矩阵

通过表2 的混淆矩阵，我们就可以计算出一些评价指标。其中最常见的就是正确率，通常来说，正确率越高，分类器的性能越好。但是由于分类器对少数类的不敏感，当对不平衡数据进行分类时，少数类在很大程度上被判为多数类，导致少数类样本的识别率较低，因此正确率不适用于评价不平衡问题［14］。本文选用其它目前常用于评价不平衡问题的指标G-mean和F-measure 。

G-mean表示只有当分类器对样本中少数类和多数类的分类效果都很好的情况下，此时G-mean的值最大［14～15］。定义如下：

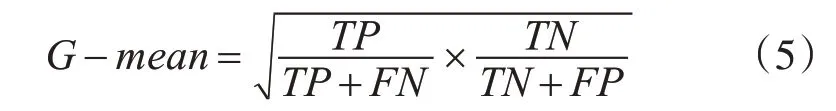
F-measure 同时结合了精确度和召回率，是它们的加权调和平均，用于最大限度地提高对单个类性能的评价程度，因此可用于测量分类器在少数类样本上的分类性能。定义如下：

4.3 实验结果分析

本文的对比实验主要包括三个算法的对比，分别是SMOTE、Borderline-SMOTE 和本文提出的BN-SMOTE 算法。为了测试这些算法在不同分类器下的效果，在通过算法对三组数据集过采样处理结束后，分别利用SVM 和C4.5 决策树对合成后的数据集进行分类，最终得到G-mean 和F-measure值对结果进行评价。

4.3.1 实验环境和相关参数设置

本文实验环境为操作系统Windows 8 64 bit，CPU/Intel（R）Core（TM）i5-3210M 双核处理器，主频2.5GHz，内存8G，硬盘容量1T，编译工具Python 3.6.0。其中SVM 算法核函数使用RBF 核函数，系数σ＝0.5，惩罚因子cost=2。对于BN-SMOTE 算法，设置k1=5，k2=3，k3=|Smin|/2，所有的这些值都是在一些初步运行后的选择。对于SMOTE 和Borderline-SMOTE算法，近邻个数k值都设置为5，同时评价指标F-measure 中的β取值为1，即F-Value。为避免数据重复计算，客观评价算法的性能，实验均采用10 次10 折交叉验证的平均值作为数值结果［16］。

4.3.2 实验结果对比

表3 为各算法（SMOTE、Borderline-SMOTE、BN-SMOTE）分 别 在SVM 和C4.5 决 策 树 下 的F-Value、G-mean 结果对比。从三组不平衡数据集（Abalone、Pima、Phoneme）的实验中可以看出，在SVM 分类器下，三个算法的F-Value 值相差不大，各有优劣，但BN-SMOTE 的G-mean 值要大于其它两个算法，而在C4.5 决策树分类器下，三个算法中BN-SMOTE 算 法 的F-Value 和G-mean 都 明 显 更高，由此可知无论在SVM 和C4.5 决策树中，BN-SMOTE 算法的表现都不差甚至更好。同时在对同一数据集的实验中，我们发现BN-SMOTE 算法在C4.5 决策树下的表现要更优于在SVM 分类器下的表现。

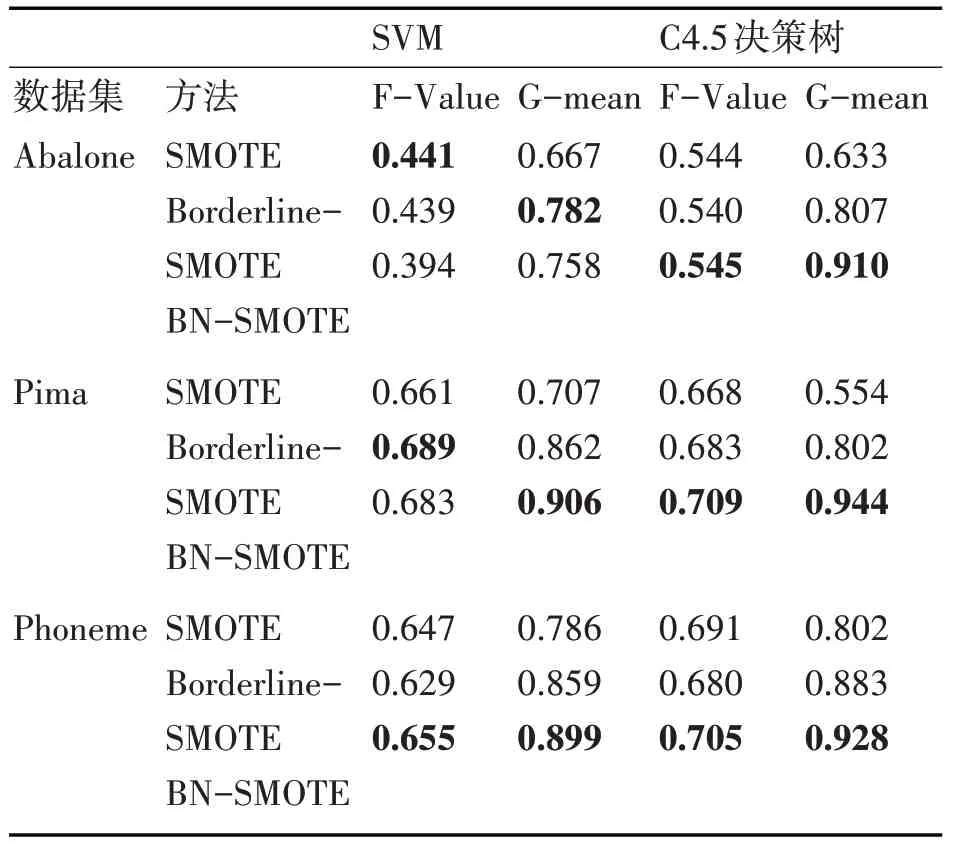
表3 SVM分类器下不同算法的F-Value和G-mean对比

4.3.3 实验结果与过采样率N的关系

图2～4 分 别 表 示 的 是 在Abalone、Pima、Pho⁃neme 数据集的实验中，G-mean 关于采样率N 的变化情况。对于Abalone 数据集，当采样率N=3 时，BN-SMOTE 算法在SVM 和C4.5 决策树中达到最大值，此时数据集内部达到类别平衡的状态，而随着采样率N 的增大，分类精度逐渐减少，原因是少数类样本的不断增多而产生了新的不平衡。同时从图2（a）和图2（b）对比中可以看出，BN-SMOTE 算法在C4.5 决策树中表现明显更好于SVM。同理在Pima 数 据 集 中N=4，Phoneme 数 据 集N=8 时，BN-SMOTE算法达到最大值，且整体表现优于其它两个算法。因此从以上分析中可以得出结论：1）当采样率N接近于数据集的不平衡率，此时数据集趋于平衡，分类效果最好；2）BN-SMOTE 算法在分类器C4.5决策树中的表现更好。

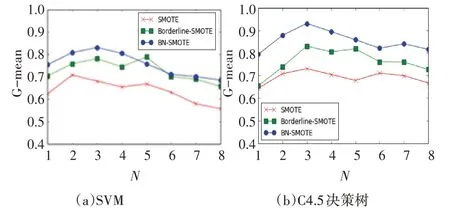
图2 Abalone的G-mean关于采样率N的变化曲线

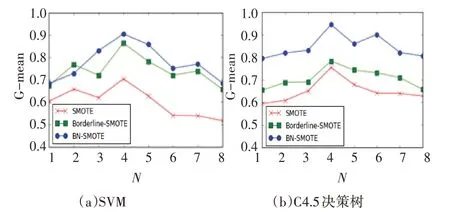
图3 Pima的G-mean关于采样率N的变化曲线

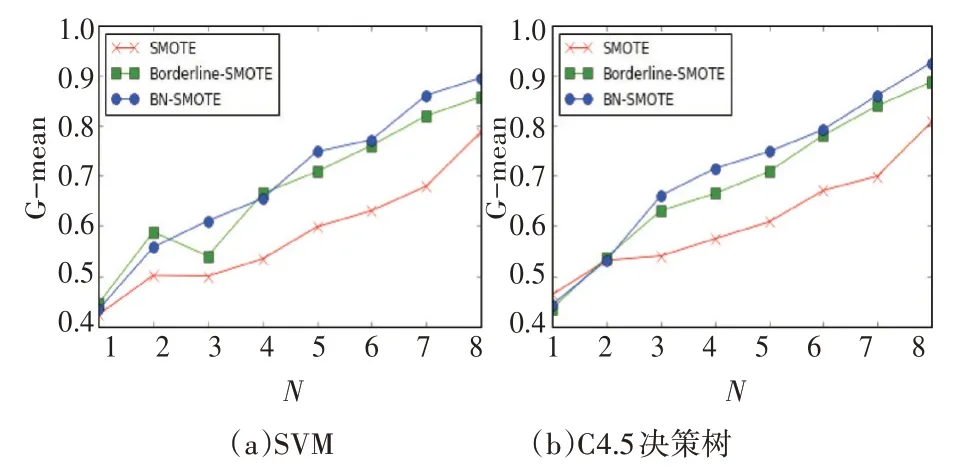
图4 Phoneme的G-mean关于采样率N的变化曲线

5 结语

本文进行了广泛的实验对BN-SMOTE 在不同数据集上的表现进行评估，并与其他方法比较，实验表明无论在SVM 和C4.5 决策树中，该算法都具有很好的表现。本文的后续工作主要有两点：一是考虑使用名义特征的数据集，在本文中，我们只选用了具有连续的特征的数据集，因此可以使BN-SMOTE 通用化来处理任何类型的特征；二是BN-SMOTE 可以与其他一些欠采样和边界估计方法集成，以研究它们是否能够比单个BN-SMOTE过采样提供更好的结果。