基于改进蚁群算法的信息SNP 选择算法研究∗
顾 鑫 陈伟鹤 张付全 张 婷 蒋跃明
(1.江苏大学计算机科学与通信工程学院 镇江 212013)(2.无锡市精神卫生中心 无锡 214151)(3.无锡市妇幼保健院 无锡 214002)(4.无锡市第五人民医院 无锡 214073)
1 引言
遗传疾病是指由于遗传物质发生改变而引发的疾病,目前遗传疾病主要分为复杂疾病和单基因疾病两种,复杂疾病主要包括精神分裂症和哮喘病等,主要是因为基因中的多个单核胆酸多态性之间的相互作用而形成的,而单基因疾病则是遵循孟德尔遗传定律。
近年来,随着DNA 微阵列技术的不断进步,作为检测人类常见疾病的遗传变异的工具,基因组范围的关联研究也受到了很大的关注。单核苷酸多态性(Single Nucleotide Polymorphism,SNP)是指基因组水平上由于单核苷酸变异所引起的序列多态性。SNP 拥有数量多、分布范围广和稳定度高等特点,常被用于复杂性状的疾病、群体的基因识别和遗传解剖等方面的研究,因此,SNP 已经成为第三代遗传标记。对SNP的广泛研究,使得像类风湿关节病和精神分裂症等疾病的研究取得了良好的进展[1]。然而,大量研究发现两个无关个体的99.9%的基因组序列是相似的。而剩余的0.1%的差异是导致人体产生疾病的关键所在[2~3],因此对冗余的SNP 进行筛选,即从大量的SNP 中选择具有代表性的信息SNP成为一个重要的课题。
不同遗传标记之间存在非随机组合的现象,例如多代遗传中的SNP,即标记不是完全独立的。这种现象通常存在于各种物种中,我们将这种现象称为连锁不平衡(LD)。在对SNP 进行筛选时,考虑到SNP维度较高以及SNP之间存在连锁不平衡性的特点,使得传统的机器学习方法在解决它时难免会遗漏掉许多内在的遗传信息。针对上述场景,结合上述SNP 的特点,本文提出一种基于改进蚁群算法的SNP选择方法,设计合理的路径选择函数和信息素更新机制,同时将连锁不平衡性引入蚁群算法。
2 相关工作
目前,国内外的相关研究主要是通过生物实验的方法从样本中获取SNP的原始数据,如果单纯采用生物学的方法进行基因分型,将会面临消耗时间长,代价昂贵以及难以满足生物分析数据的要求[4~5]。当前的SNP 选择方法有很多,比较成熟的有两类:基于单块的方法和基于单体型重构的信息SNP方法。
2.1 基于单体型块的方法
考虑到理论数量远大于人类单体型数量的基本事实,通过设定一个评价指标来衡量每个SNP,将基因组序列数据分成多个离散的单元型块,然后根据相应的规则在每个块中选择相应的信息SNP。Patil 首先提出了使用贪心算法来划分奇异块的想法[6]。Chang 等提出了混合贪婪-划分树的方法,该方法引入了分支算法定界的思想,一个原始信息SNP选择问题被划分为多个独立的子问题,最后构建出贪婪划分树[7]。Liao 提出一种多次蚁群算法选择SNP集合,通过计算复杂度和噪声影响同时提高划分准确率,试验结果表明该方法有一定改进[8]。Prathibh 提出了一种基于遗传算法的特征选择算法,该算法减少了特征数量,提高了基因/SNP组的特异性[9]。
2.2 基于单体型重构的方法
Bafna[10]及Halldorsson[11]首先提出了一种基于单倍型重构的SNP位点选择方法。Halperin[12]等描述了一种用于SNP 预测和选择的新方法STAMPA,该方法可以不必提前执行区块划分,因此使得方法的应用范围更加广阔。Lee[13]提出了基于SNP 之间的条件独立性来标记SNP选择的方法,通过构建贝叶斯网络,选择独立和预测性高的SNP的一个子集。Ilhan[14]提出采用克隆选择算法选择SNP 子集,其中SNPs 之间的相似性关联被用作其余SNP的预测方法,能够更快的识别SNP。Alzubi[15]提出了基于条件互信息最大化和支持向量机特征递归消除融合的混合特征选择方法,取得了较高的重构准确度。
3 基于蚁群算法的SNP选择方法
根据SNP 数据分布特点和信息SNP 选择的难点,本文提出基于改进蚁群算法的信息SNP 选择方法,设计合理的路径选择函数和信息素更新机制。为了避免信息素的过分累积,从而引发局部最优,提出对信息素进行挥发,同时将连锁不平衡性引入蚁群算法的启发式函数,从而对SNP选择方法进行改进。
3.1 基于改进蚁群算法的SNP子集构造
3.1.1 连锁不平衡
目前已有多种连锁不平衡性的测量指标,包括两位点和多位点。以下为二等位基因位点的连锁不平衡度量方法,假定两个SNP位点的四种数据频率分别为f11,f12,f21,f22,它们满足式(1):
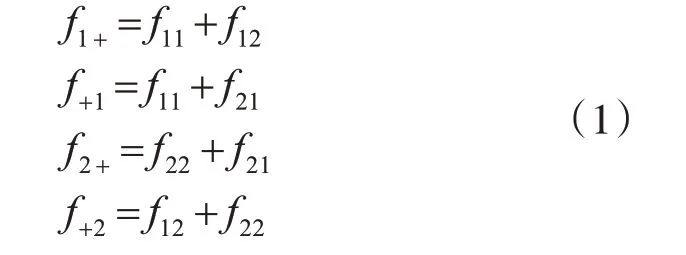
其中,f1+标识第一个等位基因为1 的单体型的频率之和,那么连锁不平衡度量方法如式(2)所示:

两点连锁度量D 值范围太大[16],具有相似连锁分布的位点组合之间的D 值将会变得更大。改进的策略是对该值作归一化后再进行度量,如式(3)所示:
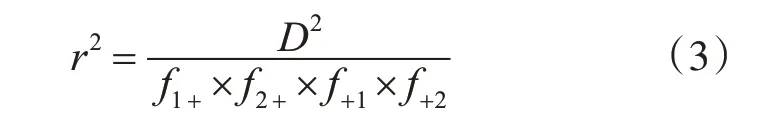
此时r2的取值位于0~1 之间。研究发现,r2能直接反应关联研究效能,因此当前大多方法采用它作为选择代表性SNP的依据。
3.1.2 蚁群算法基本原理
蚁群算法最初由意大利学者Dorigo M。于1991 年首次提出,它本质上是一个由仿生学计算构建的群优化系统。蚁群算法具有天然的分布式计算机制、较强的鲁棒性和易与其他优化算法结合的特点。
在觅食的过程中,蚂蚁将会根据信息素的浓度来决定移动的方向。因此,当环境中没有信息素时,蚂蚁的行为将是完全随机的。而在接下来的过程中,一条路径上经过的蚂蚁越多,那么这条路径上积累的信息素也就越多,之后的其他蚂蚁因此更有可能选择这条路径,该过程逐渐由随机行为转变为智能行为。
3.1.3 路径选择函数
信息SNP 选择问题中候选子集的质量取决于两个因素:信息SNP 数量和信息SNP 对非信息SNP 重新构造的准确度。本文将这两种因素放在路径选择及信息素更新过程中。蚂蚁的路径选择采用概率机制,当前人工蚂蚁选择下一节点的概率如式(4)所示:
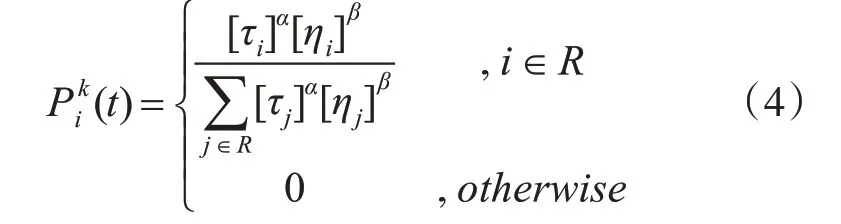
其中τi和ηi分别表示节点信息素浓度和节点当前的启发信息,而α和β分别为信息素和启发因子的权重参数,R 表示本次迭代过程中没有被选中的SNP 位点。可以通过调整权重的方式更新选择机制,如当α>β时,表示蚁群选择路径更侧重于参考SNP位点上的信息素浓度。
3.1.4 信息素更新机制
信息SNP 选择问题中信息SNP 数量大小可以类比于传统蚂蚁在觅食过程中走过的路程,路程的长度越短则表明SNP 该条路径越优秀。在相同的重新构造准确度下,信息SNP 的数量越小,SNP 子集越好,位点上的信息素类似于自然界中蚂蚁留下的化学物质。信息素累积函数如式(5)所示:
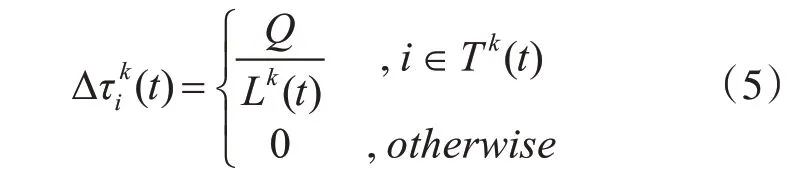
其中,Tk(t)表示第k只蚂蚁在第t 次迭代过程中所构造的候选信息SNP 子集,Q为原始数据集中的所有SNP 数量。Lk(t)表示路径的长度,即子集中包含的SNP数量。
信息SNP 选择问题也与天然蚂蚁觅食过程不同,信息SNP选择过程是跳跃的,相反,蚂蚁可以从当前节点跳转到任何其他节点,并且构造的候选子集具有无序性,即选择SNP的顺序不影响子集的质量。
为了防止信息素在某些位置叠加并引起局部最优,必须适当削弱位点的信息素。本文模拟自然环境中的空气流动,引入了信息素挥发机制,通过式(6)实施蚂蚁和信息素蒸发添加新信息素:

∆τi( )
t表示迭代后式(2)中在所具有的信息素,并且被设置为路径上的总信息素的初始值。
信息素挥发系数ρ是蚂蚁留在路径上的信息素的持久权重,挥发系数越小表示信息素每次迭代过程中损失越小,信息素越不容易消失,留下的信息素越多。通过调整挥发系数,可以在一定程度上降低信息素的过度累积,从而尽量避免蚁群算法在后期陷入局部最优。考虑到该算法在初始阶段较差的寻优能力,在得到更好的解后引起局部最优,因此提出一种新的信息素挥发因子。具体调整如式(7)所示:
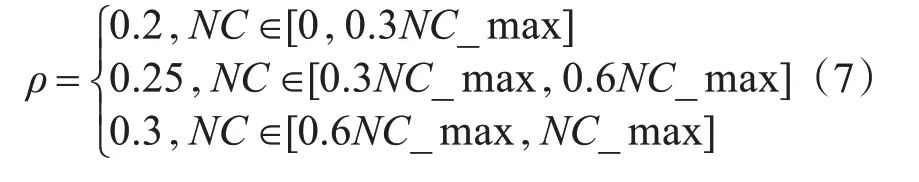
式(7)中,NC_MAX 表示蚁群算法的最大迭代次数,为固定值。NC 表示蚁群算法在本轮的迭代次数。在迭代初期,通过设定较小的信息素挥发系数可以加快收敛速度,而在算法的中期和末期,适当增加信息素挥发系数的值避免局部最优。
3.1.5 启发式函数
信息SNP 子集的优劣可以由重构准确度来测量,其中Ci为两位点连锁不平衡度量,如式(8)所示:

本文中两位点连锁测量使用式(3)的r2。其中表示两个位点i 和j 之间的连锁值,而n表示已经选中位点的数目,Ci为位点i和已经选中位点的连锁值的平均值,介于0~1 之间。值越大,该位点具有更强的连锁性,则更有利于成为信息SNP。
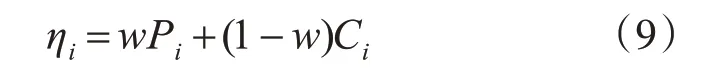
Pi表示信息位点i 对其它所有非信息SNP 位点重构准确度的平均值。将Pi和Ci的加权组合作为启发式信息,修改w的值可以调整Pi和Ci权重。
3.1.6 蚁群算法构造信息SNP子集的伪代码
以下使用伪代码来描述用于选SNP 子集的蚁群算法的总体框架。当方法达到最大迭代次数或达到重构准确度时退出。
基于蚁群算法的信息SNP 子集构造
输入:个体基因型数据或单倍型数据
输出:信息SNP 集合
Begin:
初始化信息素和参数;
Nc=0;
While(Nc<=Nc_max)
For i=1 to n_ants //n_ants为蚂蚁数量
//每只蚂蚁分别逐个添加SNP到候选信息SNP
While(prediction accuracy is not enough)
计算ηi;
按式(4)在候选SNP选择新的SNP位点;
End while
保存本次迭代过程中的最优解;
End For
2.1 两组血浆NT-proBNP水平比较 病例组患儿的NT-proBNP水平在治疗3 d、治疗7d 、治疗14 d时均显著低于组内治疗前(F=176.405,P<0.05),病例组患儿的NT-proBNP水平在治疗前、治疗3 d、治疗7 d、治疗14 d时均显著高于对照组(F=286.557,P<0.05)。见表1。
//每只蚂蚁结束寻找路径后,根据已经经过的节点数目
计算这些节点上每只蚂蚁留下的信息素
按式(6)计算新的信息素;
Nc++;
End while
返回候选SNP;
End
3.2 基于KNN的SNP预测
本文采用K-最近邻(KNN)方法来预测未选择的SNP。给定测试集d(其类别未知),该方法是在训练集中查找k 个最近邻居,并且使用k 个最近邻居的类别来对候选者进行预测。在本文中,两个SNP 基因序列之间的距离为汉明距离,必须确定基因型之间k 个最近的邻居。本文设定为5-NN(k=5),即确定投票过程的基因型样本的5 个邻居,并通过对这五个邻居进行投票获得预测样本结果。整体过程如图1所示。
4 实验
4.1 实验数据和环境
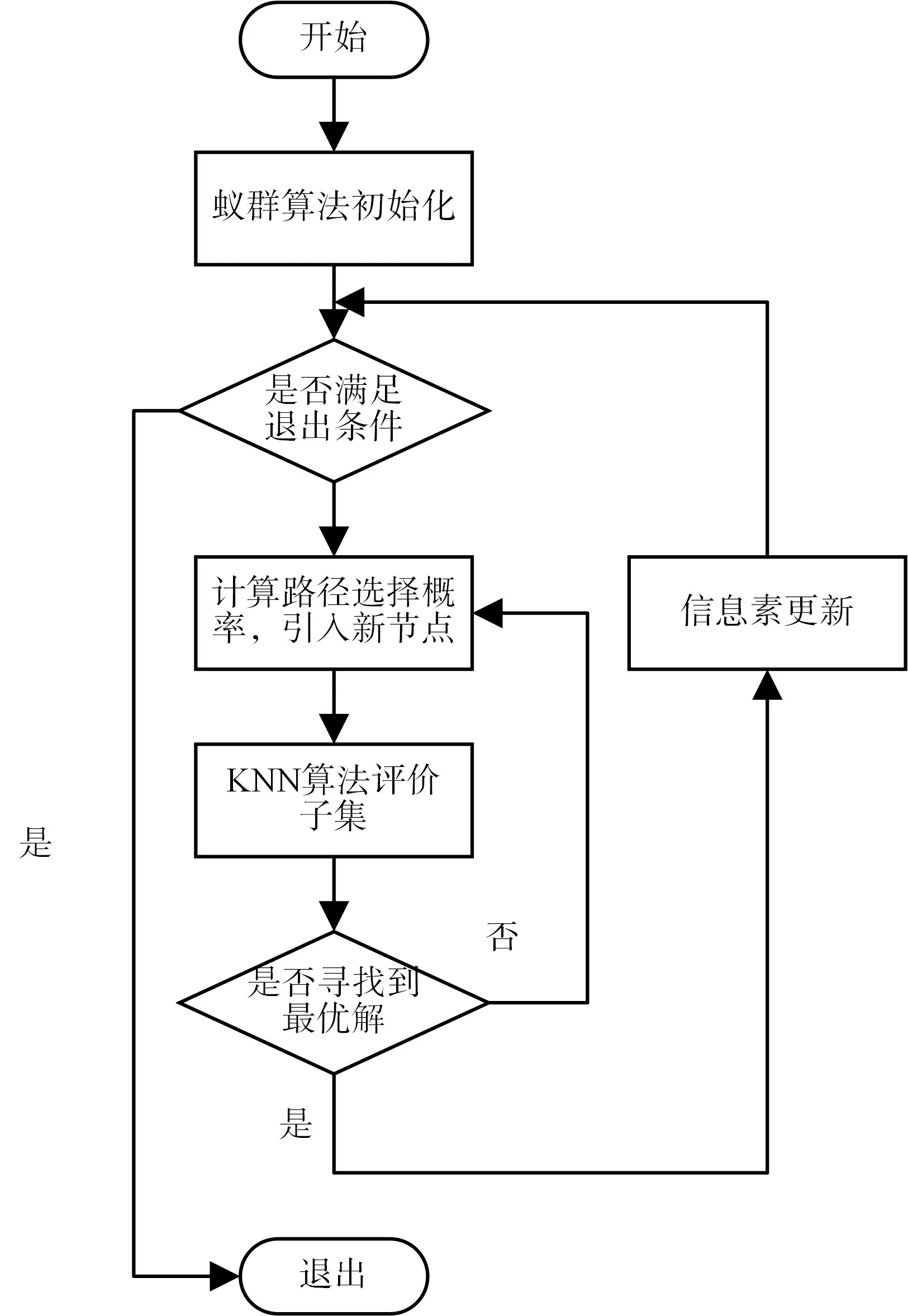
图1 SNP选择流程图
实验数据本实验中所使用的数据由无锡市精神卫生中心提供。数据格式为遗传病的SNP 基因型格式,并且每个样本都带有标记信息,标记样本是否患病。数据集的概况描述如表1所示。

表1 数据集描述
4.2 实验评价指标
本文使用信息SNP 子集对非信息SNP 子集的重构准确度(ACC(I))作为信息SNP子集的评价指标,其定义如式(10)所示:

其中gi为位点上的实际值,为预测出的值,两者差的绝对值即为预测误差。N 是样本的数量,是非信息SNP 的数量,两者积为总重构次数。重构度越高,信息SNP子集对非信息SNP的预测效果越好。
4.3 SNP数据编码
由于实验的原始数据是SNP的基因型表示,本次实验采用的编码方式是“0-1-2”编码,分别表示AA、Aa以及aa。编码完成后,对缺失值需要进一步进行填充。考虑到SNP局部可能存在关联性,所以使用K近邻的方式对其进行填充。
4.4 实验结果与分析
Halperin 等设计了一种最大投票法STAMPA,将此方法用于对结果的重构,每个位点根据其最相似的信息SNP 位点预测[18]。粒子群算法BPSO[19]类似于本文中候选子集构造的蚁群算法,BPSO 和STAMPA 组合为BPSO/STAMPA,与MLR 的组合是BPSO/MLR,本文方法蚁群算法与最近邻分类组合标记为ACO/KNN,蚁群算法参数设置为α=1、β=3,蚂蚁数量设置为10,迭代次数为10。
4.4.1 重构准确度
三种方法在两个数据集上的实验结果如图2和图3 所示。在图中,横坐标是信息SNP 的数量,纵坐标是重构准确率。可以看出,在该数据集E144 中,所提出的方法和BPSO/MLR 的准确度明显优于BPSO/ STAMPA,ACO/KNN 与BPSO/MLR的重构准确度效果相似。在数据集G1000中,该方法具有比BPSO/STAMPA 和BPSO/MLR 的更高的重构准确度,并且重构准确度平均高出2%~5%。BP⁃SO/MLR 略高于BPSO/STAMPA,ACO/KNN 引入了连锁度,使得位点间的连锁不平衡性较高。可以得出本文方法更能获取有利于样本重构的特征。

图2 数据集E144上重构准确度
4.4.2 运行时间
分别使用ACO/KNN、BPSO/STAMPA 和BPSO/MLR 三种算法在两个数据集上进行实验,并比较每种算法的运行时间,其结果如图4和图5所示(每组实验重复三次并对结果取均值)。在图中,横坐标是信息SNP 的数量,纵坐标是运行时间(单位:s)。由于E144 数据集规模大于G1000 数据集,因此运行时间也大于G1000 数据集。从图中可以看出,随着SNP 数量的增加,该方法的优势也逐渐明显。
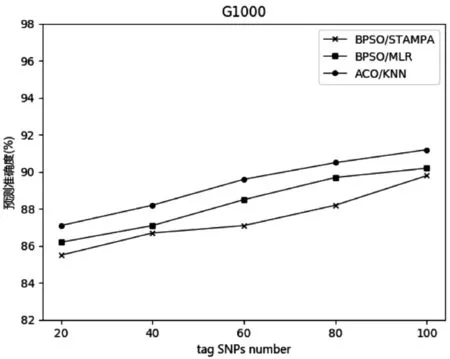
图3 数据集G1000上重构准确度
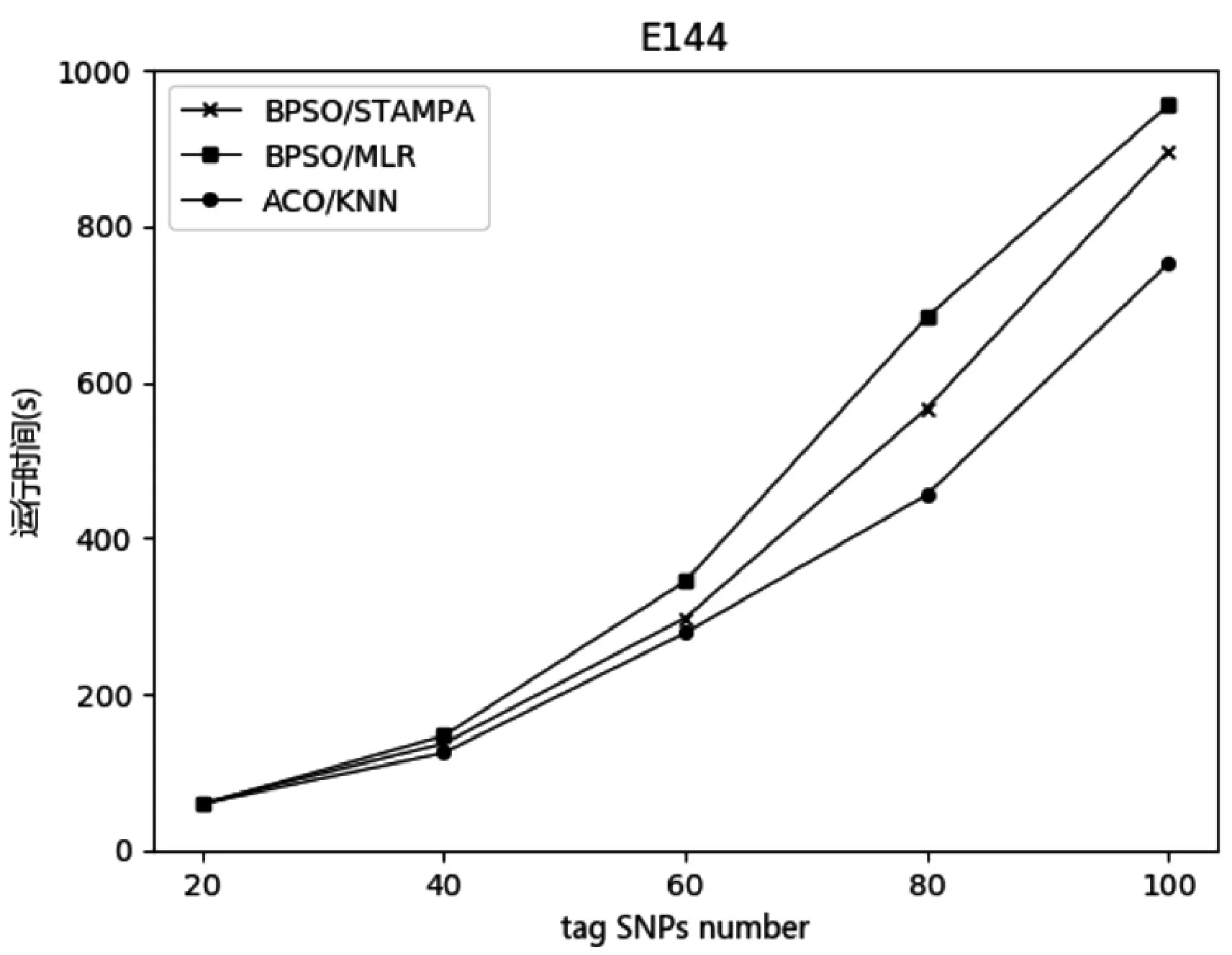
图4 数据集E144上运行时间
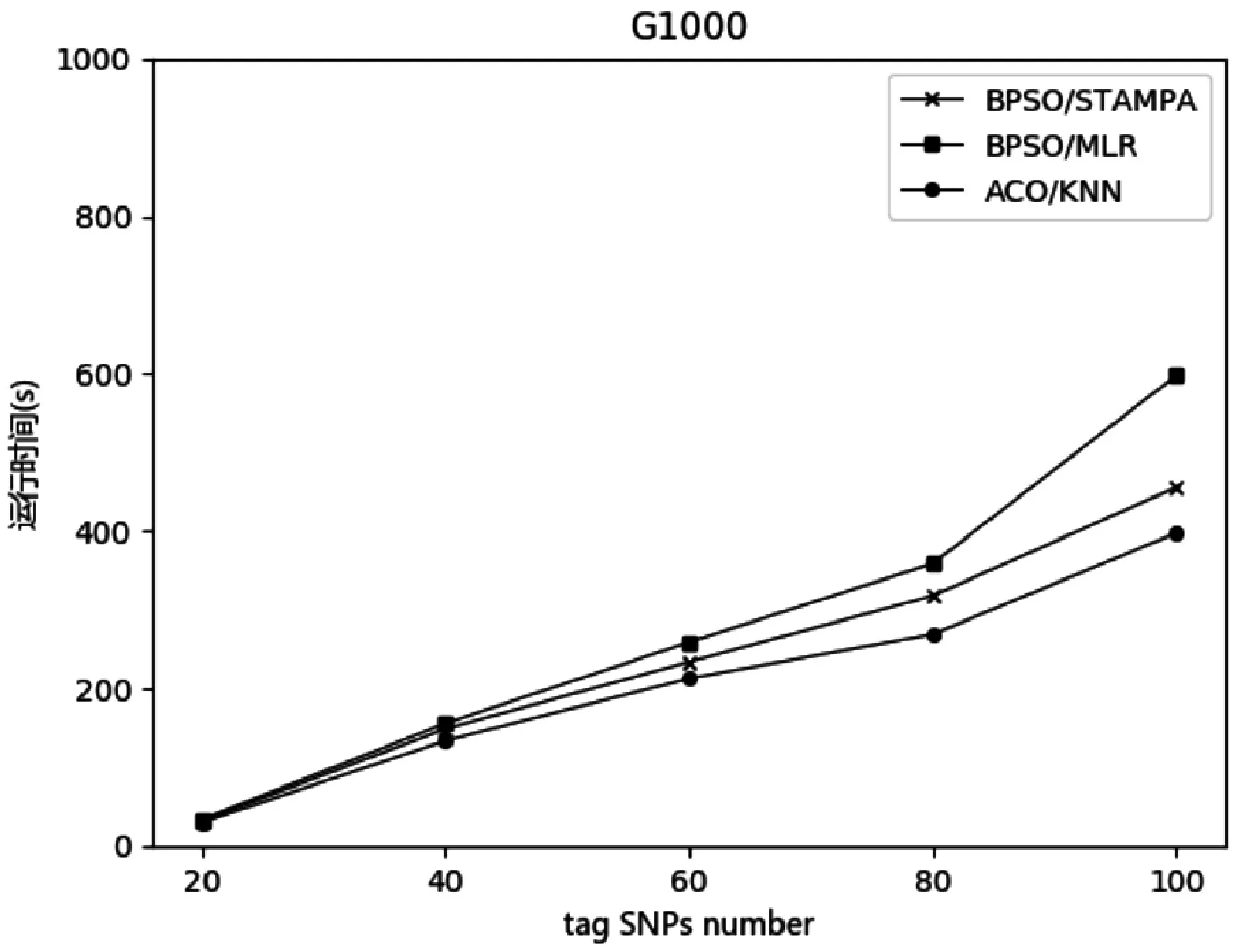
图5 数据集G1000上运行时间
5 结语
在本文中,针对SNP 数据普遍存在的少样本、高维度的问题,和不同SNP位点之间存在连锁不平衡导致的位点之间具有强相关性的特点,将连锁不平衡性应用到蚁群算法中,提出一种基于蚁群算法(ACO)信息SNP 选择方法。本文使用的实验数据来自无锡市精神卫生中心,并与文献中的SNP选择方法作了比较。本文的后续工作是对KNN 进行改进,使筛选出的信息SNP子集具有更高的重构度。

