基于多元线性回归的学生成绩分析∗

张 晓 李晓戈

（西安邮电大学计算机学院 西安 710121）

1 引言

在互联网+时代，我国高校的办学规模不断扩大［1］，高校的信息化建设也在逐步完善。与此同时随着数据挖掘技术的深层次应用，数据挖掘技术也逐渐应用到高校教学管理中［2］。高校招生规模日益扩大，传统教学管理模式面临巨大的挑战，在转型高校中的体现愈发明显。高校的教学管理系统在高校的教学管理中发挥着越来越重要的作用［3］。但是目前的教务管理系统只是实现了数据的存储、查询、统计等功能［4］，没有进一步挖掘数据中有价值的信息。以我校的学生成绩管理系统为例，该系统只实现了对学生成绩的简单查询和数理统计，利用这种方法得到的数据只是计算机技术的简单应用，无法发现影响学生成绩的具体因素［5］，以及各种因素之间的关系。如何有效地分析以往的学生成绩数据，从中挖掘潜在的学生成绩的影响因素［6］，不断提高高校的教学质量，成为所有高校教学管理的核心内容。

本文首先利用数据挖掘软件Weka［7］对榆林学院信息工程学院2003～2015 学年计算机科学与技术专业的722 名学生成绩进行关联规则分析，猜想课程之间是否存在关联性，企图能找出学生所学习的课程之间存在的一些关联规则；然后利用数据挖掘软件Wake 对榆林学院信息工程学院2003～2015学年计算机科学与技术专业的722 名学生成绩进行多元线性回归分析，猜想基础课程对与之相关的专业课是否会产生影响，企图能找出学生所学习的基础课程对与之相关的专业课会产生怎样的影响。

2 数据与方法

2.1 数据

本文的研究数据来源于榆林学院教务管理系统，并与学校管理者签订了保密协议，原始数据是榆林学院信息工程学院2003～2015 学年的学生成绩，本次数据的预处理是通过Microsoft Excel2010除去科目中的公共选修课和某些公共必修课，本次数据中未发现空值。

利用数据挖掘软件Wake对学生成绩进行关联规则挖掘和多元线性回归分析，从原始数据中选出计算机科学与技术专业2003～2015 学年所学习的五门基础课和七门专业课共十二门课程：五门基础课分别是C 语言程序设计、大学英语、高等数学、大学物理和线性代数，并分别用A、B、C、D 和E 表示；七门专业课分别是操作系统、汇编语言程序设计、计算机网络、计算机组成原理、离散数学、数据结构和数据库原理，并分别用F、G、H、I、J、K 和L 表示，在表1中列出。

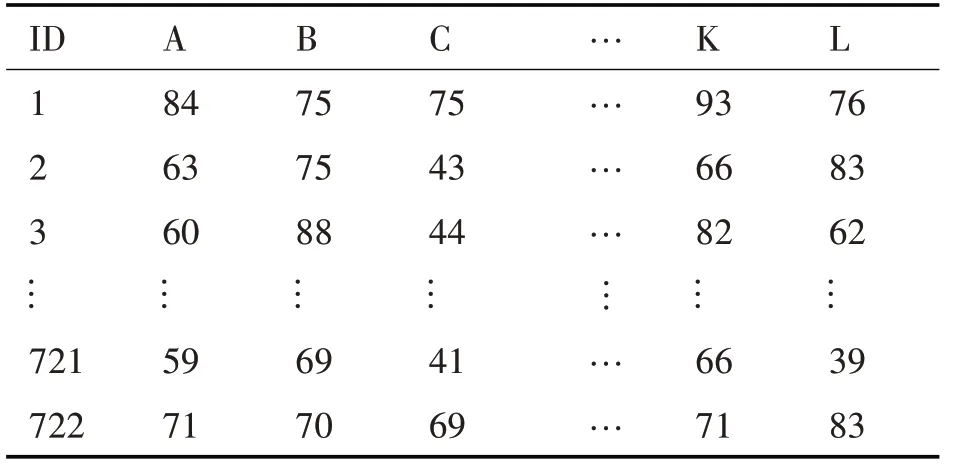
表1 十二门课程的学生成绩

关联规则挖掘必须要将被研究的数据进行离散化［8］处理，对研究数据进行手动离散化和概念分层［9］。首先，将十二门课程的学生成绩分成三段，分别是0～60 分，60～80 分，80～100 分，并进行分段标记。以C 语言程序设计为例，C 语言程序设计0～60 分，60～80 分，80～100 分分别标记为A3，A2，A1。在进行手动离散化和概念分层之后的数据，在表2中列出。

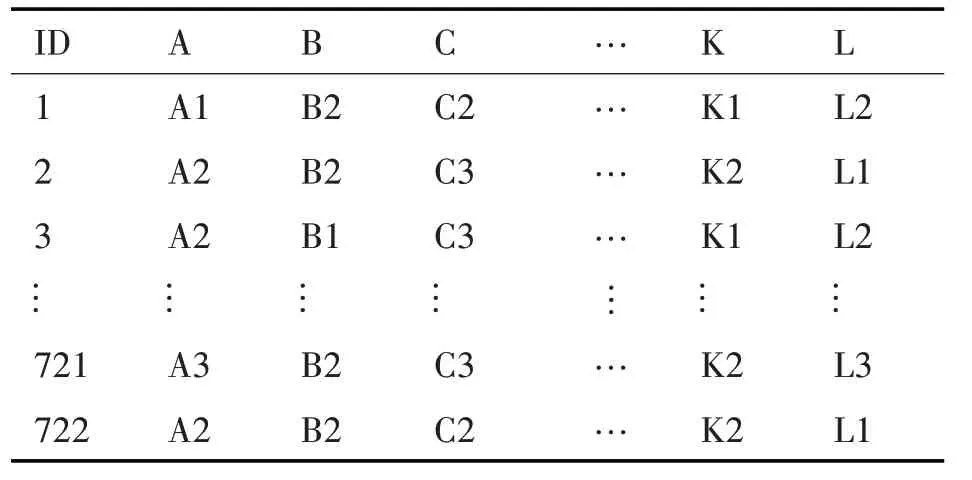
表2 对十二门课程进行离散化和概念分层

利用多元线性回归分析，挖掘基础课程对专业课程是否会产生影响。将五门基础课与其中一门专业课的数据多元线性回归分析，以汇编语言程序设计为例，即筛选出C 语言程序设计、大学英语、高等数学、大学物理、线性代数和汇编语言程序设计，在表3中列出。

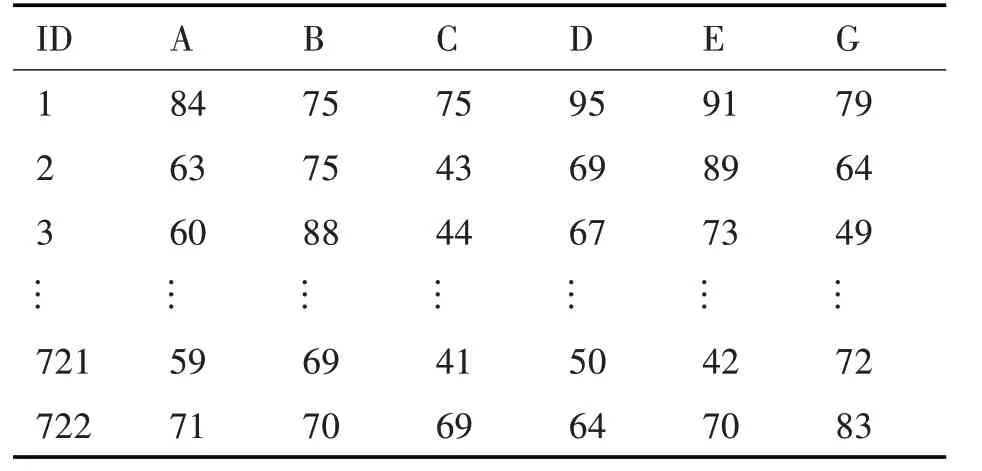
表3 基础课和汇编语言程序的成绩

2.2 方法

2.2.1 关联规则介绍

关联规则挖掘是发现大量数据中项集之间有趣关联或相关联系［10］。实现关联的技术主要是统计学中的支持度和置信度分析［11］，支持度主要用于测量连接分析中的统计在数据集中的重要性，置信度用于测量连接分析中的可信度［12］。支持度即在事物集U中不仅出现项集A又出现项集B的事务为a%，则关联规则A==＞B 的支持度为a%，即表示A和B在事务U中出现的频率，式（1）列出

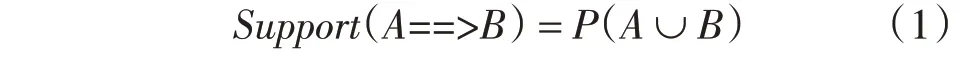
置信度即在事务U中出现项集A的同时项集B也出现的概率，表示关联规则的强度，式（2），式（3）列出

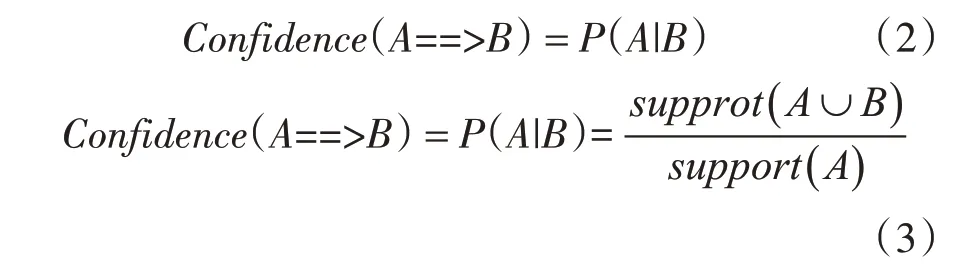
关联规则的算法有很多，本文主要采用的是关联规则的经典算法Apriori算法［13］，该算法使用一种逐层搜索的迭代方法：N 项集用于搜索（N+1）项集。首先，找到频繁1 项集的集合，记作M1，M1 用于找到频繁2 项集的M2，而M2 用于找到M3，如此下去，直到不能找到频繁N 项集，每一次搜索都需要扫描一次数据库，为提高频繁项集逐层产生的效率，一般作法是利用Apriori 算法的性质压缩收缩空间［13］。Apriori 算法的性质是频繁项集的所有非空子集必须也是频繁的。

2.2.2 多元线性回归介绍

回归分析是从一组数据出发通过一个或一些变量的变化解释另一个变量的变化［14］。首先根据对实际问题的分析判断，将变量分为解释变量和非解释变量；其次，根据函数拟合方式，确定合适的数学模型来描述变量间的关系，再在统计拟合的准则下确定模型的参数，建立回归方程。由于涉及到的变量是不确定的，回归方程是在样本数据的基础上得出，必须进行回归模型的统计检验，经统计检验后，再根据回归模型，进行因变量的预测。

回归分析的类型分为一元线性回归和多元线性回归，本文主要采用的是多元线性回归。多元线性回归的基本模型

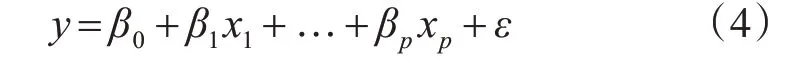
其中x1，x2，…，xp是自变量，β0，β1，…，βp是未知参数，ε是零均值随机变量。

如果对式（4）两边求期望，则有多元线性回归方程

估计未知参数β0，β1，…，βp是多元线性回归分析的核心任务之一。由于参数估计的工作是基于样本数据的，由此得到的参数只是参数真值的估计值，记为，，…，。最终解得模型（4）的多元经验回归方程

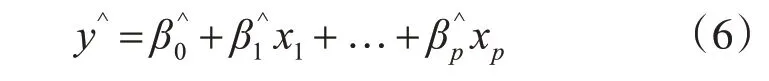
多元回归模型中的检验有两种，一种是回归系数的显著性检验，即是检验某个变量xi的系数是否为零；另一种检验就是回归方程的显著性检验［15］，即是检验改组数据是否使用于线性方程做回归。

3 基于数据挖掘技术的学生成绩分析

3.1 利用关联规则挖掘对学生成绩的挖掘结果

将已经过离散化和概念分层的数据在挖掘软件Wake 使用Apriori 算法进行训练，在训练中不断调整参数设置，其中classIndex 是类属性索引，delta是迭代递减单位，LowerMinSup 指的是最小支持度下界，MinMetric 指的是度量的最小值，SigLevel 指的是重要程度，进行重要性测试，upperMinSup指的是最小支持度上界，最终参数修改结果在表4 中列出。

表4 关联规则挖掘参数设置

最终得到榆林学院信息工程学院计算机科学与技术专业所学课程中的十二门课程之间的关联规则，在表5中列出。

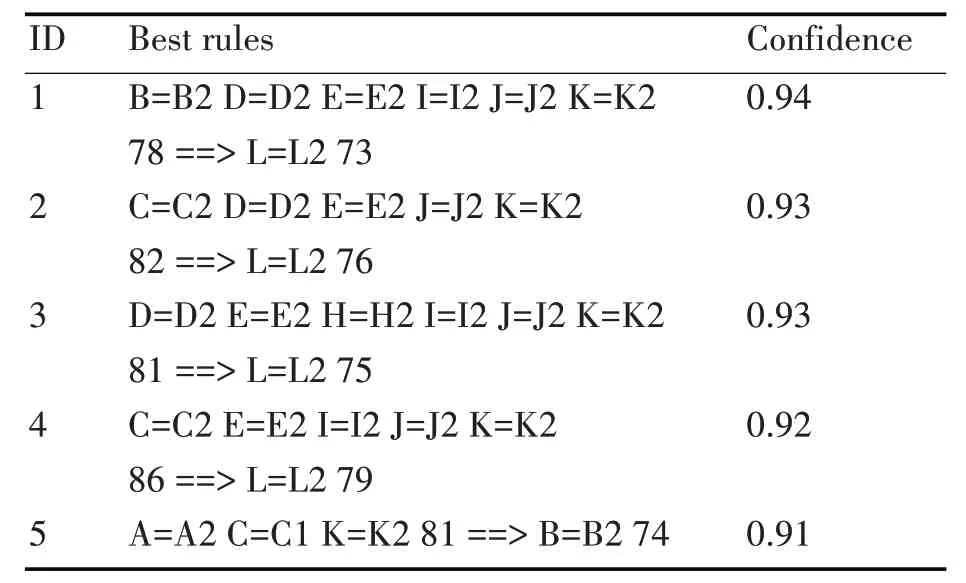
表5 关联规则挖掘结果

通过对十二门课程进行关联规则挖掘得到的规则分析有：1）如果大学英语、大学物理、线性代数、计算机组成原理、离散数学、数据结构的成绩均在60～80 分之间，那么数据库原理的成绩在60～80分之间有94%的可能性；2）如果高等数学、大学物理、线性代数、离散数学、数据结构的成绩均在60-80 分之间，那么数据库原理的成绩在60～80 分之间有93%的可能性；3）如果大学物理、线性代数、计算机网络、计算机组成原理、离散数学、离散数学数据结构的成绩均在60～80 分之间，那么数据库原理的成绩在60～80 分之间有93%的可能性；4）如果高等数学、线性代数、计算机组成原理、离散数学、数据结构的成绩均在60～80 分之间，那么数据库原理的成绩在60～80 分之间有92%的可能性；5）如果C 语言程序设计、高等数学、数据结构的成绩均在60～80 分之间，那么大学英语的成绩在60～80 分之间有91%的可能性。

综上所述，数据库原理的成绩与大学英语、高等数学、大学物理、线性代数、计算机网络、计算机组成原理、离散数学和数据结构的成绩有关系；大学英语的成绩与C 语言程序设计、大学英语、高等数学、计算机网络、计算机组成原理和数据结构的成绩有关系。

3.2 利用多元线性回归分析对学生成绩的挖掘结果

将研究数据在Wake 中选择Linear Regression算法，使用默认参数，选择Cross-validation，设置Folds 为20，即使用其中的20 条数据进行交叉验证。并分别对F列、G列、H列、I列、J列、K列和L列的数据进行预测。

根据上述对多元线性回归建立回归模型的分析，可对本次研究的数据建立模型：

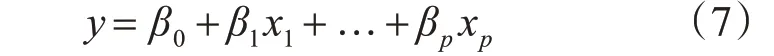
其中自变量x1、x2、x3、x4和x5分别代表C 语言程序设计、大学英语、高等数学、大学物理和线性代数，因变量y1、y2、y3、y4、y5、y6和y7分别代表操作系统、汇编语言程序设计、计算机网络、计算机组成原理、离散数学、数据结构和数据库原理。预测的多元线性回归模型在表6中列出。

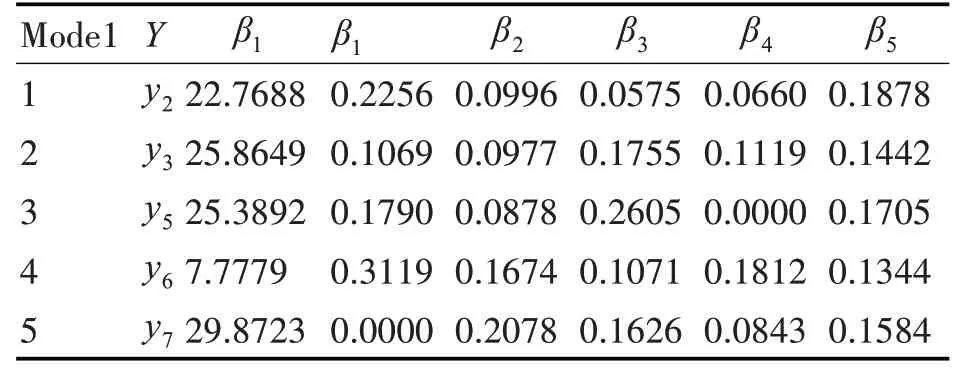
表6 多元线性回归模型

回归模型的好坏由模型评价参数来说明，R、MAE、RMSE、RAE 和RRSE 分别代表的是相关系数、平均绝对误差、均方根误差、相对误差绝对值和根相对误差，模型评价参数在表7中列出。

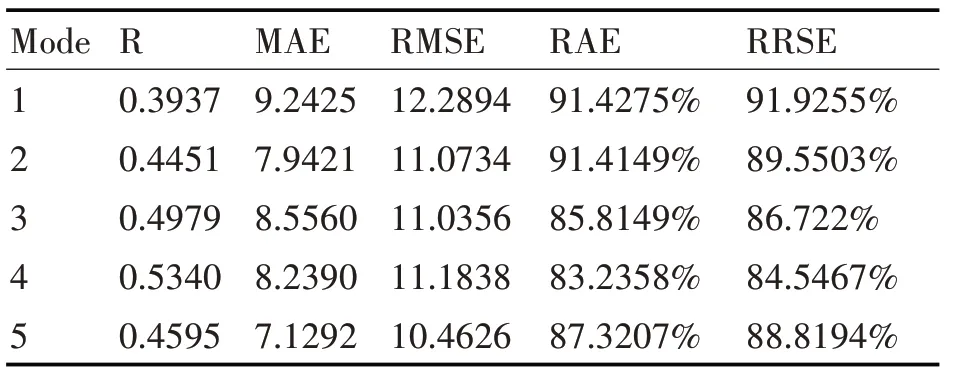
表7 回归模型评价参数

针对线性回归模型与回归模型性能指标，可得到结果有：1）汇编语言程序设计会受到基础课程C语言程序设计、线性代数、大学英语、大学物理和高等数学的影响，其中对其影响较大的基础课程是C语言程序设计和线性代数；2）计算机网络会受到基础课程高等数学、线性代数、大学物理、C 语言程序设计、和大学英语的影响，其中影响较大的基础课程是高等数学和线性代数；3）离散数学会受到基础高等数学、C 语言程序设计、线性代数和大学英语的影响，其中影响较大的基础课程是高等数学和C语言程序设计；4）数据结构会受到基础课程C 语言程序设计、大学物理、大学英语、线性代数和高等数学的影响，其中影响较大的基础课程是C 语言程序设计和大学物理；5）数据库原理会受到基础课程大学英语、高等数学、线性代数和大学物理，其中影响较大的基础课程是大学英语和高等数学。

综上所述，数学类专业课受数学类基础课的影响较大，比如高等数学对离散数学的影响就很大；计算机类专业课受计算机类基础课的影响较大，比如C 语言程序设计对汇编语言程序设计的影响就很大；计算机类和数学类相结合的课程会同时受计算机类和数学类基础课的影响，比如C 语言程序设计和线性代数对操作系统的影响就很大。

4 结语

本文主要通过数据挖掘软件Wake对学生成绩进行了关联规则挖掘和多元线性回归建模，并给出了参数设置和模型评价参数，分别得到了课程与课程之间的关联和基础课程对专业课程的影响。基于数据挖掘技术的学生成绩分析是一个比较广泛的课题，在利用关联规则挖掘学生成绩时，只是对课程之间的相关性进行了分析，没有加入一些附加因素，比如，学生的性别、年龄、年级和英语等级考试成绩等学生基本信息。在利用多元线性回归对学生成绩建立回归模型时，只是分析了基础课程对专业课程的影响，没有建立学生平时成绩对考研成绩的回归模型。以上这些不足之处将会在下一步的研究工作中得到完善与优化。