含负项top-k高效用项集挖掘算法
孙 蕊,韩 萌,张春砚,申明尧,杜诗语
(北方民族大学计算机科学与工程学院,银川 750021)
0 引言
近年来,数据挖掘技术引起了信息产业的极大关注。其中,频繁项集挖掘是数据挖掘的重要组成部分之一。频繁项集[1]的目标是发现满足最小支持度阈值的所有项集。但是,在实际应用中,频繁项集挖掘算法具有一定的局限性。它假定所有项具有相等的价值,并且每个项在每次事务中出现的次数不超过一次。但是,这两个假设在现实生活中不是普遍存在的。例如,客户购买6袋面包和1台电脑,客户购买多个相同的商品非常普遍,而出售面包和电脑的利润却有所不同。为了解决这一问题,研究人员提出了高效用项集挖掘算法。高效用项集(High Utility Iteme,HUI)[2]挖掘算法的主要目标是通过考虑用户的偏好(例如利润、数量和成本)来挖掘效用值高的项集。高效用项集挖掘算法克服了频繁项集挖掘算法带来的限制,在挖掘过程中,项的数量可能出现多次,并且每个项都有不同的价值。由于高效用项集挖掘算法缺乏向下闭合属性,因此搜索空间很难缩小。随后,Liu等[2]提出了一种Two-Phase算法,该算法使用向下闭合属性来减小搜索空间,并有效地找到高效用项集。随后,研究人员提出了IHUP(Incremental High Utility Pattern)[3]、TWU(Transaction Weighted Utility)-Mining[4]、IIDS(Isolated Items Discarding Strategy)[5]、UP-Growth(Utility Pattern Growth)[6]、UP-Growth+[7]算法。但是,以上提出的算法在挖掘过程中会生成大量的候选项集,这导致了算法执行时间长和内存消耗大的问题。Liu等[8]提出了一阶段HUI-Miner(High Utility Itemset Miner)算法,该算法依赖效用列表结构,可以有效地修剪大部分搜索空间。
对于高效用项集挖掘算法,研究人员进行了许多研究。但是,绝大多数算法都是挖掘含有正效用的项集。在现实生活中,负效用项集也起着重要作用。例如,当客户去超市购买计算机时,客户可以免费获得键盘和鼠标。假设超市从每台计算机上获利50美元,键盘和鼠标损失2美元,那么超市最终营利48美元。因此,负效用在现实生活中也具有重要意义。但是,大多数高效用项集挖掘算法都只挖掘正效用项集,如果用该类算法挖掘负效用项集,则会出现结果集遗漏问题。
针对传统的高效用项集挖掘算法只能挖掘正效用项集的局限性,研究人员提出了挖掘单位利润为负效用项集的算法。但是,在挖掘高效用项集时,最小效用阈值的设置问题始终是一个挑战。如果最小效用阈值设置得太低,将产生大量的高效用项集,这将降低用户使用效率;如果最小效用阈值设置得太高,将生成很少的高效用项集,这将无法满足用户的需求;反复调整最小效用阈值将花费大量的时间。
为了克服这些局限,本文提出了含负项top-k高效用项集(Top-kHigh utility itemsets with Negative items,THN)挖掘算法。该算法不需要设置最小效用阈值,只需要设置k值,就能得到用户需求效用值最高的项集结果集合。本文的主要工作如下:
1)提出含负项top-k高效用项集挖掘算法——THN,该算法可以解决在挖掘同时含有正项和负项项集时需要设置最小效用阈值的问题;
2)该算法采用模式增长方法,使用重新定义的子树效用和重新定义的本地效用修剪大量没有希望的候选项集;该算法利用事务合并和数据集投影技术,提高了算法的时空性能;为了加快效用计数过程,该算法利用效用数组计数技术计算项集效用;
3)该算法提出了自动提升最小效用阈值的策略,实验结果表明,该策略可以明显减少算法的执行时间。
1 相关工作
目前,国内外研究者对含负项高效用项集挖掘算法和top-k高效用项集挖掘算法进行了研究。
1.1 含负项高效用项集
针对传统的高效用项集挖掘算法只能挖掘含正项集的局限性,2009年Chu等[9]提出含负项的高效用项集挖掘算法HUINIV(High Utility Itemsets with Negative Item Values)-Mine。HUINIV-Mine算法是Two-Phase算法的扩展,它需要在内存中维护大量的项集,因此这严重影响了算法的效率。2011年,Li等[10]提出了MHUI-BIT(Mining High-Utility Itemsets based on BITvector)、MHUI-TID(Mining High-Utility Itemsets based on TIDlist)算法来挖掘含负项的高效用项集。但是,该算法还是存在产生候选项集过多的问题。Lin等[11]随后提出了FHN(Faster High utility itemset miner with Negative unit profits)算法,该算法使用深度优先的搜索策略,并使用基于效用列表的EUCS(Estimated Utility Co-occurrence Structure)来有效地修剪搜索空间。实验结果表明,FHN算法的执行时间是HUINIVMine算法的1/500,内存消耗是它的1/250。2014年,Lan等[12]提出了TS-HOUN(Three-Scan mining approach to efficiently find High On-shelf Utility itemset with Negative profit values)算法,该算法提出挖掘同时考虑货架时间和含负项集的高效用项集。TS-HOUN算法采用三阶段挖掘方法,在每个时间段挖掘项集,然后使用合并操作合并每个时间段的项集。由于多次扫描数据集,因此TS-HOUN效率很低。
为了解决多次扫描数据集的问题,FOSHU(Faster On-Shelf High Utility itemset miner)[13]算法使用了基于效用列表的结构,该结构同时挖掘所有时间段的项集。实验结果表明,FOSHU算法的执行时间是TS-HOUN算法的千分之一,FOSHU算法的内存消耗是TS-HOUN算法的十分之一。2017年,Dam等[14]提出了FOSHU的扩展算法KOSHU(top-KOn-Shelf High Utility itemset miner)。2015年,Subramanian等[15]提出 了UP-GNIV(Utility Pattern-Growth approach for Negative Item Values)算法来挖掘含负项的高效用项集。2017年,Xu等[16]提出了HUSP-NIV(High Utility Sequential Patterns with Negative Item Values)算法,该算法用于挖掘含负项的高效用序列项集。2017年,Krishnamoorthy等[17]提出挖掘含负项的高效用项集挖掘算法——GHUM(Generalized High Utility Mining),GHUM比FHN快一个数量级。2017年,Gan等[18]提出 了HUPNU(High Utility patterns with both Positive and Negative unit profits from Uncertain data)算法,用于从不确定数据集中挖掘含负项的高效用项集。2018年,Singh等[19]提出了EHIN(Efficient High-utility Itemsets mining with Negative utility)算法来挖掘含负项的高效用项集,EHIN算法提出了多种有效的数据结构和修剪策略。同年,Singh等[20]提出了CHN(Closed High utility itemsets mining with Negative utility)算法来挖掘含负项闭合高效用项集。2019年,Singh等[21]提出了EHNL(Efficient High utility itemsets mining with Negative utility and Length constraints)算法来挖掘含负项和长度约束的高效用项集。
尽管上述所有的算法都可以挖掘含负项的高效用项集,但是难以解决挖掘出满足用户需求的高效用项集数量的问题。
1.2 top-k高效用项集
top-k高效用项集挖掘算法不需要设置最小效用阈值,直接根据用户设置的高效用项集数量k进行挖掘。最早的top-k高效用项集挖掘算法是TKU(Top-KUtility itemsets mining)[22],它是UP-Growth算法的扩展。TKU算法采用Two-Phase模型:在第一阶段,该算法使用多种策略来提高内部的最小效用阈值,并对搜索空间进行修剪,生成潜在的top-k高效用项集;在第二阶段,从潜在的top-k高效用项集集合中识别真正的top-k高效用项集。TKU算法使用SE(Sorting candidates and raising threshold by the Exact utility of candidates)策略对候选项集进行排序并提高内部最小效用阈值。为了提高TKU的性能,Ryang等[23]提出了一种名为REPT(Raising threshold with Exact and Pre-calculated utilities for Top-khigh utility pattern mining)的算法,REPT算法依赖于UP(Utility Pattern)-Tree结构,通过使用额外的策略来快速提高边界最小效用阈值,从而提高TKU的性能。由于TKU和REPT算法遵循Two-Phase模型,所以它们仍然产生了大量的候选项集。Zihayat等[24]提出了T-HUDS(Top-kHigh Utility patterns over sliding windows of a Data Stream)算法,用于在数据流上挖掘top-k高效用项集,THUDS提出了一种新的前缀效用模型,该模型采用HUDS(High Utility patterns over sliding windows of a Data Stream)-tree的压缩数据结构。陈明福[25]提出了缩小候选项集TKDC(Top-Kpattern mining with Decreased Candidate)算法,该算法节省了大量的运行时间。
为了克服两阶段算法的局限性,研究者提出了一阶段高效用项集挖掘算法。Lu等[26]提出了在数据流中挖掘top-k高效用项集的TOPK-SW(Sliding Window based TOP-K)算法,该算法将每批数据存储在当前窗口中,并将项的效用信息存储在HUI-Tree中,而无需再次扫描数据集。王乐等[27]提出了一种TOPKHUP(TOP-kHigh Utility Pattern)算法,该算法有效地将项集和项集效用信息保存到HUP-Tree中,从而确保可以直接挖掘top-k高效用项集。Tseng等[28]提出了TKO(Top-Kutility itemsets in One phase)算法来挖掘top-k高效用项集,TKO利用了HUI-Miner的效用列表结构,还提出了新的剪枝策略RUC(Raising the threshold by the Utilities of Candidates)、RUZ(Reducing estimated Utility values by using Z-elements)和EPB(Exploring the most Promising Branches first)来提高算法的性能。实验结果表明,该算法的性能优于TKU和REPT算法。Duong等[29]提出一阶段算法kHMC(top-kHigh utility itemset Mining using Co-occurrence pruning),它依赖于效用列表结构,采用多种策略提升最小效用阈值。Singh等[30]提出了TKEH(Efficient algorithm for mining Top-KHigh utility itemsets)算法,该算法使用事务合并和数据集投影技术来降低数据集扫描的成本。Kumari等[31]提出了TKRHU(Top-KRegular High Utility itemset)算法,该算法使用RUL(Regular Utility-Lists)效用列表结构来存储每个规则表的规则信息和效用信息。Krishnamoorthy等[32]提出THUI(top-kHigh Utility Itemset)高效用项集挖掘算法,该算法使用LIU(Leaf Itemset Utility)结构来提高挖掘效率。实验结果表明,在大型、密集和事务平均长度较长的数据集上具有更好的性能。
top-k高效用项集挖掘算法虽然可以不需要设置最小效用阈值就可以挖掘出用户需求的高效用项集的数量,但是目前还没有出现top-k高效用项集挖掘算法挖掘含负项的项集。
2 基本概念
事务数据集D由众多事务组成,每条事务包含一些项,每条事务都由唯一的事务标识符Tid表示。I={i1,i2,…,in}指的是出现在事务数据集D中的不同项的集合。如表1所示,事务数据集D包含7条事务D={T1,T2,…,T7}和5个项I={A,B,C,D,E}。事务Tj∈D中项x的内部效用指的是事务Tj中x的数量,表示为IU(x,Tj)。事务Tj∈D中项x的外部效用指的是事务Tj中x的利润,表示为EU(x)。如表1所示,事务T1中项A的内部效用为2;表2显示了项的外部效用值,其中项A的外部效用值为2。

表1 事务数据集Tab.1 Transaction dataset

表2 外部效用值Tab.2 External utility values
定义1 项在事务中的效用[2]。项x在事务Tj中的效用定义为U(x,Tj)=IU(x,Tj)×EU(x)。
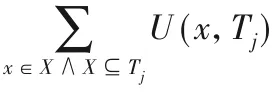



例如,TWU(D)=TU(D,T1)+TU(D,T3)+TU(D,T4)+TU(D,T6)=5+9+9+14=37。
定义6 高效用项集[2]。假定min_util是用户设置的最小效用阈值。如果项集X的效用值不小于min_util,则项集X是高效用项集;否则,它是一个低效用项集。
定义7 top-k高效用项集[22]。按照项集效用值从高到低的顺序排序,令min_util为第k个项集的效用值。对于项集X,如果条件项集X的效用值不小于min_util,则项集X称为top-k高效用项集。
2.1 负项的属性和定义
在传统的高效用项集挖掘算法中,大多数都是挖掘含有正项的项集。但是,挖掘含有负项的高效用项集时,研究者提出了几种处理负项集的属性和定义。
属性1 项集中的正效用和负效用之间的关系[9]。对于任何项集X,假定putil(X)表示事务或数据集中项集X的正效用之和,并假定nutil(X)表示事务或数据集中项集X的负效用之和。U(X)=putil(X)+nutil(X)。从以上属性可以得到,putil(X)≥U(X)≥nutil(X)。
基本原理 项集X中效用值为正的项只能提高项集X的效用,而效用值为负的项只能降低项集X的效用。因此,属性putil(X)≥U(X)≥nutil(X)成立。
属性2 使用正效用对项集的效用上限[9]。项集X的效用上限为putil(X)。
基本原理 因为U(X)=putil(X)+nutil(X),而nutil(X)是要减小U(X),所以上述推理成立。
传统的高效用项集挖掘算法使用TWU属性来修剪搜索空间。但是,TWU属性不能修剪含有负项的项集,因为TWU属性假定修剪时不存在含有负项。为了解决这一挑战,HUINIV-Mine[9]重新定义了相关概念。
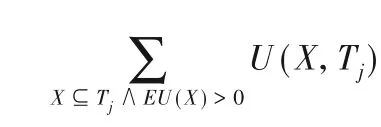
例如,事务T2的重新定义的事务效用为RTU(T2)=U(C,T2)+U(E,T2)=5+1=6。通过添加仅计算重新定义的事务效用的项来增加了正项效果。表4显示了每条事务的事务效用和重新定义的事务效用。

表4 事务效用和重新定义的事务效用Tab.4 Transaction utility and redefined transaction utility

例如,RTWU(A)=RTU(A,T1)+RTU(A,T5)+RTU(A,T6)=11+4+17=32。
使用重新定义的事务加权效用修剪搜索空间,可以找到含负项高效用项集的完整高效用项集。事务中的项按总顺序排序,因为RTWU按升序排序。
定义10 项集的扩展[19]。如果Y=α∪{X}(其中X∈2E(α),X不能为空),则项集α可以扩展为项集Y(Y出现在集合枚举树的重新定义的子树中)。另外,项集α扩展了单个项集Y(Y是集合枚举树中α的子代)。其中X∈E(α),Y=α∪{X}。在运行的示例中,α={B},集合E(α)为{C,D},词典α的单项展开为{B,C}和{B,D},α的其他扩展是{B,C,D}。
定义11 负项的扩展项集[19]。项集α可以扩展到项集Y,其中Y=α∪{X},并且X是含负项的一组项。
基本原理α∪{X}仅以少于或等于包含项集α的事务数量发生。项集X包含正项项集,并且其扩展可能大于或等于或小于项集X的效用。项集X包含负项项集,并且其扩展必须小于项集X的效用。从上面的描述,可以得出结论,如果项集X的效用值不小于min_util,则将负项集添加到项集X。如果扩展项集X的效用值仍大于或等于min_util,则该项集为高效用项集。
2.2 剪枝策略
THN算法采用重新定义的本地效用和重新定义的子树效用对搜索空间进行了有效的修剪,基于这两种方法该算法的效率得到了有效地提升。

属性3 基于重新定义本地效用的高估[19]。对于项集α和项x,其中x∈E(α)。令x可以是α的扩展,即x∈X。因此,RLU(α,x)≥U(X)始终成立。详细证明见文献[14]。
这是使用重新定义的本地效用修剪搜索空间的方法。对于项集α和项x,其中x∈E(α)。如果RLU(α,x) 属性4 基于重新定义子树效用的高估[19]。令项集α和项x,其中x∈E(α)。RSU(α,x)的效用值大于等于U(α∪{x}),则相应的取值。其中,RSU(α,x)≥U(x)保持α∪{x}的扩展X。 使用RSU修剪空间。设项集α和项x,其中x∈E(α)。如果RSU(α,x)小于min_util,则将项集扩展为单项(α∪{x}),并扩展低子树效用值。此外,在集合枚举树中修剪α∪{x}的子树,可以修剪项集α的子树。 目前,高效用项集挖掘算法在挖掘高效用项集时通常使用剩余效用进行剪枝。在利用剩余效用进行剪枝的过程中,如果项集α带有项x的效用小于min_util,则只删除子节点。在利用重新定义的子树效用进行剪枝的过程中,如果项集α带有项x的效用小于min_util,则删除子项集。因此,使用重新定义的子树效用进行修剪时,将极大地提高算法的性能。 定义14 主要项和次要项[19]。对于项集α,项集α的主要项表示为Primary(α)={x|x∈E(α)∧RSU(α,x)≥min_util}。项 集α的 次 要 项 表 示 为Secondary(α)={x|x∈E(α)∧RLU(α,x)≥min_util}。其 中RLU(α,x)≥RSU(α,x),因此Primary(α)⊆Secondary(α)。 本章详细介绍了THN算法,包括使用的事务合并和投影数据集技术、使用效用数组计算效用上界的方法、提出的阈值提升策略和THN算法的伪代码。 该算法利用事务合并和数据集投影技术减小数据集的大小,从而降低了数据集的扫描成本。投影数据集只被扫描一次,以合并相同的事务。 表5 事务合并后的数据集Tab.5 Dataset after transaction merging 定义16 投影数据集[19]。对于项集α,投影数据集D表示为α-D,定义为α⁃D={α⁃T|T∈D∧α⁃T≠0}。 为了进一步压缩数据集,本文算法需要合并投影数据集中的事务。投影事务合并比原始事务合并产生更高的数据集缩减量,因为投影事务比原始事务小,因此,投影事务更有可能是相同的。 表6 项C投影数据集Tab.6 Projected dataset of item C 表7 事务合并投影后的数据集Tab.7 Dataset after transaction merging projection 为了减小数据集的大小,需要使用事务合并技术。实现此技术的主要问题是识别相同的事务。为了实现这一点,本文算法需要相互比较所有的事务。将所有事务与每个事务进行比较的技术并不是一种有效的技术。为了解决这个问题,本文算法可以采用文献[33]中提出的相同事务排序技术≻T。这种排序技术在计算上并不昂贵。 定义18 事务的总顺序[33]。在事务数据集D中,当向后读取事务时,总顺序≻T被定义为字典顺序。有关≻T的更多阐述可以参考文献[33]。 为了降低数据集扫描的成本,THN算法使用了事务合并和数据集投影技术。当数据集包含相同的事务时,事务合并技术识别这些相同的事务,并将其替换为单条事务。事务合并技术是减小数据集大小的理想方法。数据集投影技术使较长的事务变得较短,当搜索较长的项集时,投影数据集的大小也会减小,从而降低了数据集扫描成本。目前,FHN算法使用垂直数据集且没有使用事务合并技术。 定义19 效用数组[19]。I是数据集D中出现的一组项,UA是一个长度为||I的数组,其中每个项x∈I都有一个表示为UA[x]的条目。每个条目称为UA,用于存储效用值。 1)用UA计算RLU(α)。 首先,UA初始化为0。其次,对于数据集D的每个事务Tj,所有项x∈Tj∩E(α)的UA[x]计算为UA[x]=UA[x]+U(α,T)+RU(α,T)。扫 描 数 据 集 后,UA[x]包 含RLU(α,k),∀k∈E(α)。 2)用UA计算RSU(α)。 top-k高效用项集挖掘算法的主要问题局限是,没有预先提供min_util,运行时的min_util从0或1开始,这严重降低了算法的效率。因此,这为如何自动提升min_util而不丢失任何高效用项集带来了巨大的挑战。为了解决这个问题,本文提出了有效的RTWU_strategy阈值提升策略。 RTWU_strategy阈值提升策略的详细过程如下所述。首先,在第一次扫描事务数据集时,计算此过程中所有项的RTWU(x)。例如,项A同时出现在事务T1、T5和T6中。项A在事务T1、T5和T6中的RTWU为RTWU(A)=RTU(T1)+RTU(T5)+RTU(T6)=32。根据此方法,计算所有项的RTWU(x)。然后,令RTWU={RTWU1,RTWU2,…,RTWUn}为I中项的效用列表。接下来根据定义18中的排序规则,对RTWU效用列表进行排序。然后,RTWU_strategy将已排序的RTWU效用列表中的min_util提升到第k个最大值。现在,使用这个新值作为min_util。例如,假设用户将k值设置为5,然后扫描数据集并计算项的RTWU(x)。假设效用列表中RTWU的第5个值是88,那么,min_util提高到88。然后,该算法使用这个新的min_util。最后,直至找到用户需求的效用值最高的前k个项集,RTWU_strategy阈值提升策略的伪代码如算法1所示。 算法1 RTWU_strategy。 输入:所有项的RTWU集合,k:所需的高效用项集的数量; 输出:提升min_util。 1)SortRTWUvalues; 2)Setmin_utilto thekthlargestRTWUvalue; 3)returnmin_util. 本文提出的THN算法利用了前面介绍的几种策略。算法2为主算法,将事务数据集D和用户定义的高效用项集的数量k作为输入,输出是top-k高效用项集。 第1)至4)行分别表示初始化α为空项集,ρ表示一组正项集,η表示一组负项集,将min_util初始化为1。第5)行创建创建一个k大小的优先队列(名为k_Patterns)。第6)行扫描事务数据集D,同时使用UA技术计算所有项的RLU。第7)行通过比较每个项的RLU和min_util,可以获得项集的次要项,次要项作为项集的扩展项。第8)行计算每个项的RTWU,并将结果存储在hashMap中。第9)行调用RTWU_strategy,主要功能是自动提升min_util。第10)行根据RTWU的升序对项集进行排序。注意,当按≻T顺序排序时,该算法首先考虑正效用项,然后考虑负效用项。第11)行扫描数据集D,并删除事务中不是次要项的所有项集和空事务。根据重新定义的本地效用的剪枝策略,删除的项不是高效用项集。第12)行根据字典排序对剩余事务进行排序,且正项集在负项集之前。此时,根 据EFIM(efficient algorithm for high-utility itemset mining)[33]的建议,此处执行事务合并技术。第13)行扫描数据集D,并使用UA技术计算所有项的RSU。第14)行通过比较每个项的RSU和min_util,可以获得项集的主要项。第15)行通过调用算法3从项集α开始递归执行深度优先搜索。THN算法的伪代码算法2所示。 算法2 THN算法。 输入:事务数据集D,潜在高效用项集的数量k; 输出:top-k高效用项集。 1)α←∅; 2)ρ←set of positiveutility items inD; 3)η←set of negativeutility items inD; 4)min_util←1; 5)Createa priority queuek_Patternsof sizek; 6)Scan datasetD,computeRLU(α,X)for all itemsX∈ρ,usingUA[X]; 7)Secondary(α)={X|X∈ρ∧RLU(α,X)≥min_util}; 8)ComputeRTWU(X)for all itemsk∈Iand store theseRTWUvalues them in a hashMap; 9)RTWU_strategy(hashMapRTWU,k); 10)Let≻Tbe the total order ofRTWUincreasing values onSecondary(α); 11)ScanD,remove itemx∉Secondary(α)from the transactionsTjand delete empty transactions; 12)Sort all the remaining transactions in the datasetDaccording to≻Twith positive utility items followed by negative utility items; 13)ScanD,compute theRSU(α,X)of each itemx∈Secondary(α),usingUA[x]; 14)Primary(α)={X|X∈Secondary(α)∧RSU(α,X)≥min_util}; 15)Search_P(η,α,D,Primary(α),Secondary(α),min_util,k_Patterns); 16)return top-kHUIs. 算法3的输入如下:η表示一组负项集,α为项集,α-D代表投影数据集,Primary(α)代表项集α的主要项,Secondary(α)代表项集α的次要项,min_util表示最小效用阈值,k_Patterns表示为k个项的优先级队列;输出为前k个α项集扩展的含正项高效用项集集合。 算法3第1)~2)行只能找到具有正项的扩展,每次都递归地调用自己用主要项来扩展每个次要项α。单项集的扩展技术遵循定义11。第3)行扫描数据集α-D,计算每个扩展项集β的效用,然后构造新的投影数据集β-D。在这个过程中,执行事务合并与投影数据集技术。第4)行项集β的效用值不小于min_util,然后把它添加到优先级队列k模式中。同时,将该min_util提升到优先级队列元素min_util的顶部。第6)行当项集β的效用值大于min_util,则调用算法4用负项来扩展该项集;否则,第8)行扫描投影数据集β-D,并使用UA技术计算每个项的RSU和RLU。第9~10)行找到项集β的主要和次要项。第11)~12)行算法3利用深度优先搜索的方法反复执行用主项对项集β的扩展,一直执行到满足条件为止,Search_P算法的伪代码如算法3所示。 算法3 Search_P算法。 输入:一组负项η,项集α,投影数据集α-D,α的主要项Primary(α),α的次要项Secondary(α),最小效用阈值min_util,k个项的优先级队列k_Patterns; 输出:前k个α项集扩展的含正项高效用项集集合。 1)for each itemx∈Primary(α)do; 2)β=α∪{x}; 3)Scanα-D,computeU(β),and createβ-D; 4)ifU(β)≥min_utilthen addβink_Patterns.And raise themin_utilto the top of priority queueelement’sutility; 5)end if 6)ifU(β)>min_utilthen search_N(η,β,β-D,min_util,k_Patterns); 7)end if 8)Scanβ-D,computeRSU(β,x)andRLU(β,x)where itemx∈Secondary(α),using twoUAs; 9)Primary(β)={x∈Secondary(α)|RSU(β,x)≥min_util}; 10)Secondary(β)={x∈Secondary(α)|RLU(β,x)≥min_util}; 11)search_P(η,β,β-D,Primary(β),Secondary(β),min_util,kPattens); 12)end for. 算法4的输入如下:η表示一组负项集,α为项集,α-D是投影数据集,min_util表示最小效用阈值,k_Patterns:表示k个项的优先级队列;输出为前k个α项集扩展的含负项高效用项集集合。 当项集β的效用值大于min_util时,算法4的调用条件才存在。第2)行该算法是使用负项进行扩展的。它使用定义11对所需项集负扩展的搜索空间进行修剪。第3)行扫描数据集α-D,计算每个扩展项集β的效用,然后构造新的投影数据集β-D。在这个过程中,执行事务合并与投影数据集技术。第4)行项集β的效用值不小于min_util,然后把它添加到优先级队列k模式中。同时,将该min_util提升到优先级队列元素min_util的顶部。第6)行扫描投影数据集β-D,并使用含负项UA技术计算每个项的RSU。第7)行找到项集β的主要项。第8)~9)行该算法将递归调用自身,用负项对项集β进行扩展,一直执行到满足条件为止,Search_N算法的伪代码如算法4所示。 算法4 Search_N算法。 输入:一组负项η,项集α,投影数据集α-D,最小效用阈值min_util,k个项的优先级队列k_Patterns; 输出:前k个α项集扩展的含负项高效用项集集合。 1)for each itemx∈ηdo; 2)β=α∪{x}; 3)Scanα-D,computeU(β),and createβ-D; 4)ifU(β)≥min_utilthen addβink_Patterns.And raise themin_utilto the top of priority queue element’s utility; 5)end if 6)CalculateRSU(β,x)for all itemx∈ηby scanningβ-Donce,using thenegativeUA; 7)Primary(β)={x∈η|RSU(β,x)≥min_util}; 8)search_N(β,β-D,Primary(β),min_util,k_Patterns); 9)end for. 在本节中,给出一个简单的说明性示例,以展示THN算法如何从事务数据集中找到含负项top-k高效用项集。假设如表1所示的7条事务,并且有5个项的内部效用。同时,表2显示每个项的外部效用。此外,最终挖掘出的效用值最高项集的数量k被设置为20。THN算法从事务性数据集中挖掘高效用项集,THN算法首先计算事务中每一项的效用,并找到该事务的事务效用。例如,事务T2中有3个项B、C和E,它们的内部效用值分别是1、5和1。表2中的B、C和E的外部效用分别为-3、1和1。那么T2中B、C和E的效用值可以分别计算为1*(-3)=(-3),5*1=5和1*1=1。经过上述过程,可以计算出T2的TU为(-3)+5+1=3。所有事务的TU值结果如表3所示。为了过高估计效用,THN算法使用RTU。为了找到RTU,THN算法只计算正效用值为5+1,即在T2中为6。同样,所有RTU都可以计算出来。所有事务的RTU如表4所示。RLU是使用深度优先搜索计算的。运行示例中项A的RTWU值出现在三个事务T1、T5和T6中,它们的RTU值分别为11、4和17。因此,项A的RTWU可计算为11+4+17=32。根据项的RLU不小于min_util,然后找到次要项集。Secondary={A,B,C,D,E}。在这之后,所有的项都按照RTWU升序排序,负项总是在正的项集之后。 然后,不属于次要项集的项被删除。因此,没有从示例数据集中删除任何项。同时,如果从事务中删除了所有项,则删除那些空事务。然后对剩余的事务按总顺序≻T进行排序。之后,本文提出的THN算法再次扫描数据集,计算所有项集的RSU。RSU不小于min_util的项位于主要项中。因此,Primary={A,C,D,E},只使用主要项集的项进行深度优先搜索。所有次要项集{A,C,D,E,B}的项作为每个子树的子代节点。为此,使用深度优先搜索来查找子树中的下行节点。使用算法2和算法3对节点进行挖掘,然后递归地调用算法2来扩展所有具有正项,然后调用算法3扩展具有负项。在运行的示例中,假设k值为20,最终的top-k高效用项集如表8所示。运行示例的高效用项集是{{A}:12,{C}:14,{A,C,D}:16,{C,D}:31,{A,C,D,B}:13,{C,D,B}:16,{A,C,D,E}:17,{C,D,E}:37,{A,C,D,E,B}:14,{C,D,E,B}:19,{A,D}:20,{C,E}:23,{A,D,B}:11,{D}:28,{A,D,E}:24,{D,E}:37,{A,D,E,B}:15,{D,E,B}:15,{A,E}:12,{E}:12},其中每个项集旁边的数字表示其效用值。 表8 top-k高效用项集Tab.8 top-k high utility itemsets 为了测试THN算法的性能,本文做了大量的实验。通过扩展spm f[34]上的开源Java库,可以实现该实验。该实验运行环境的CPU为3.00 GHz,内存为256 GB,操作平台是Windows 10企业版。该实验使用了六个真实的数据集mushroom、chess、accidents、pumsb、retail和kosarak,所有数据集都是从spm f上下载的。表9显示了数据集的基本特征,每一列从左到右分别表示数据集名称、事务数量、项的个数和数据集密度。 表9 数据集的基本特征Tab.9 Basic characteristicsof datasets 对于所有的数据集,项的内部效用值在1~5的范围内随机生成,项的外部效用值使用对数正态分布在-1 000~10 000生成。为确保结果的稳健性,本文所有的实验都进行了10次,并统计了平均结果。 本文为了评估所提出的技术在THN中的影响,因此检验了THN(RSU-Prune)和THN(TM)的性能。THN算法同时利用了数据集合并技术TM和剪枝策略RSU。THN(RSU-Prune)仅在TM被禁用的情况下使用修剪策略RSU。类似地,THN(TM)仅使用数据集合并技术TM,其中剪枝策略RSU是禁用这种变化。本文提出的THN算法是第一个挖掘含负项top-k高效用项集挖掘算法。因此,找不到具有相同性能的另一算法进行比较。 传统上,测试新正项的top-k高效用项集挖掘算法是将其与挖掘相同结果集并设置最佳最小效用阈值的非top-k高效用项集挖掘算法进行比较。对于新提出的THN算法,本文通过查找相关文献得出,FHN算法[11]是挖掘含负项最先进的高效用项集挖掘方法。HUINIV-Mine[9]算法也是产生负效用的高效用项集挖掘算法,但是HUINIV-Mine的执行时间在有的数据集中无法在图中画出来,因为它需要更多的执行时间和内存。因此,对比非top-k算法是HUINIV-Mine和FHN算法,这两种算法均被用于挖掘含负项高效用项集。 为了确保挖掘出相同的结果集,本文为HUINIV-Mine和FHN算法选择了最佳min_util。这样,可以以相同数量相同结果集的模式进行性能比较。为了评估性能,本文通过提高k值来执行所有数据集上的所有变化,直到所有的变化花费太多的时间或内存不足。 本节评估了THN算法和对比算法在所有数据集中的运行时间性能。图1显示了THN算法和对比算法在所有数据集的运行时间情况。从图1中可以清楚地看到,在mushroom、chess、accidents和pumsb密集数据集中,THN算法的运行时间远少于HUINIV-Mine、FHN算法。因为HUINIV-Mine在chess和accidents数据集中,即使k值设置为1,也需要耗费长达数小时的执行时间,因此在图1中没有画出。在mushroom和pumsb数据集中,当k的值设置得较大时,THN算法与HUINIV-Mine、FHN算法之间的运行时间间隔变大。在mushroom、chess、accidents和pumsb数据集中k的值小于100时,THN算法和FHN算法的运行时间没有太大差异。当k值超过500时,mushroom、chess、accidents和pumsb数据集在FHN算法中的运行时间会激增,而THN算法的运行时间则相对稳定。从图5中可以看出,数据集扫描技术和基于重新定义子树效用的剪枝技术相结合在密集数据集中得到了很好的使用。但是在mushroom、chess、accidents数据集中THN(TM)和THN(RSUPrune)总是比THN算法执行时间长,但是在pumsb数据集中THN(TM)比THN算法执行更少的时间。这种现象表明,事务合并对于具有大量不同项和项的平均长度较大的数据集执行得很好。从密集数据集中可以看出,当k值设置较高时,本文算法与FHN之间的差距较大,说明本文算法比FHN运行的k值更高。FHN的性能不好的主要原因是,它加入了较小项集的效用列表,以生成较大的项集。FHN考虑没有出现在数据集中的项集,因为它们通过合并较小的项集来探索项集的搜索空间,而不扫描数据集。由于密集的数据集包含大量的长项和事务,因此提出的THN算法性能更好。 从图1中可以清楚地看到,在retail和kosarak稀疏数据集中,FHN算法的运行时间少于HUINIV-Mine和THN算法。在retail数据集中,随着k值的增加,FHN算法的运行时间几乎不变。在retail数据集中当k的值小于500时,在kosarak数据集中当k的值小于50时,THN算法的运行时间和FHN算法的运行时间几乎持平。在retail数据集中,THN(RSU-Prune)算法的执行时间小于THN算法。这一结果表明,retail数据集不支持TM技术。Retail数据集有大量不同的项,并且比所有其他数据集有更宽的最大长度,因此它不支持TM技术。实验结果表明,在数据集高度稀疏的情况下,THN算法可以放弃TM技术,有效地挖掘高效用项集。因此,在retail和kosarak稀疏数据集中,THN(TM)算法的性能远低于FHN算法。因为稀疏数据集,它们具有大量不同的项,几乎没有相同事务。由于在稀疏数据集中,事务数据库中具有相同项的事务的概率显著降低,所以事务合并策略变得开销很大。THN算法提出的事务合并技术在高度稀疏的数据集中表现不佳,事务合并需要大量时间来合并事务,稀疏数据集中的相同事务较少,因此浪费大量时间,效率很低。 图1 不同算法的运行时间对比Fig.1 Comparison of runtimeof different algorithms 本节评估了THN算法与对比算法在所有数据集中的内存消耗的性能。图2显示了THN算法和对比算法在所有数据集的运行时间情况。 从图2中可以清楚地看到,在所有密集数据集mushroom、chess、accidents和pumsb中,THN算法的内存消耗值远低于HUINIV-Mine和FHN算法。在chess、accidents和pumsb密集数据集中,THN(TM)和THN(RSU-Prune)的内存消耗远比HUINIV-Mine和FHN算法小。随着k值的增加,FHN的内存消耗迅速增加。对于mushroom密集数据集,THN算法的内存消耗远小于HUINIV-Mine和FHN算法。但是,THN(TM)和THN(RSU-Prune)算法的内存消耗大于FHN算法。在chess和accidents数据集中,随着k值的增加,THN算法消耗的内存几乎保持不变,而FHN算法消耗的内存是THN算法消耗的内存的三倍。对于所有密集数据集,在THN算法中,TM技术和RSU技术可以更好地结合在一起。因此,THN算法比其他算法使用更少的内存。HUINIV-Mine和THN算法在大多数情况下都需要高内存,其中,因为FHN算法将所有的效用列表保存在内存中以进行连接,因此需要消耗大量的内存空间。 从图2可以清楚地看到,在稀疏数据集kosarsk中,THN算法的内存消耗远远小于HUINIV-Mine和THN算法。THN(RSU-Prune)算法的内存消耗也小于HUINIV-Mine和THN算法,可以看出RSU的剪枝策略在THN算法中得到很好的使用。但是,THN(TM)算法的内存消耗大于THN算法,可以得出在稀疏数据集kosarsk中,TM技术并不能提高内存消耗的性能。在retail数据集中,THN的内存消耗远小于HUINIV-Mine算法。但是,在k值小于500时,THN算法及其THN(TM)和THN(RSU-Prune)算法的内存消耗比FHN多。因为,retail数据集是高度稀疏的,所提出的算法对高度稀疏数据集不是有效的。THN采用的TM技术不适用于retail等高度稀疏的数据集。 图2 不同算法的内存消耗对比Fig.2 Comparison of memory usageof different algorithms 本节从算法的可扩展性角度对所有算法进行了实验。该实验选取了密集数据集accidents和稀疏数据集retail,实验数据大小20%~100%不等,k值设置为100。通过以上设置,可以更好地展示所有算法的可伸缩性。图3显示了THN算法的运行时间随着数据集大小的增加而线性增加。图4显示了THN算法随着数据集大小的增加内存消耗也线性增加,但在FHN算法中,内存消耗则急剧增加。以上实验结果表明,THN算法在不同数据集和参数下都具有可扩展性。 图3 不同算法运行时间的可扩展性Fig.3 Scalability of runtimeof different algorithms 图4 不同算法内存消耗的可扩展性Fig.4 Scalability of memory usageof different algorithms THN算法是挖掘含负项top-k高效用项集挖掘算法,使用基于RSU搜索空间的剪枝策略,为了减少数据集的扫描次数,使用了事务合并和数据投影相结合的技术。该算法在四个密集数据集和两个稀疏数据集上进行了实验。对比算法使用了本身的变形算法THN(TM)和THN(RSU-Prune),还有挖掘含有负项高效用项集挖掘算法HUINIV-Mine[9]和FHN[11]。 由于在实验中为HUINIV-Mine和FHN算法设置min_util,这对于THN算法是不公平的,因为top-k高效用项集挖掘问题总是比相应的非top-k高效用项集问题更困难。主要原因是非top-k高效用项集挖掘算法直接设置了最佳min_util,top-k高效用项集挖掘算法min_util开始为0,然后逐渐增加min_util直到找到k个项集。非top-k高效用项集挖掘算法将在此过程中减少很大一部分搜索空间。在本实验中,本文直接为HUINIV-Mine和FHN算法设置了最佳min_util,这使得该算法具有很大的优势。对于每个不同的数据集,在运行THN算法时会设置不同的k值。在不同的数据集上运行HUINIV-Mine和FHN算法之前,将min_util设置为HUINIVMine和FHN算法以挖掘k个项集中的最小效用值。 从实验结果可以看出,THN算法在mushroom、chess、accidents、pumsb和kosarak数据集的运行时间效率上有了显著提高,在retail数据集上的执行时间是可比较的。HUINIVMine算法在accidents、chess、pumsb和kosarak数据集中,因为需要太长的执行时间和内存消耗而崩溃。因此,运行时间和内存消耗没有显示。此外,THN在所有数据集上的内存改进是相当显著的。与HUINIV-Mine和FHN算法相比,THN在除retail外的所有数据集上的运行时间效率和内存消耗性能都有显著提高。 本文提出含负项top-k高效用项集挖掘算法——THN。当用户挖掘含负项高效用项集时,可以直接设置所需的项集数k,而无需反复调整min_util挖掘用户需求高效用项集的个数。THN算法是一阶段高效用项集挖掘方法,该算法使用深度优先进行搜索。为了减少数据集的扫描次数,该算法使用事务合并技术和数据集投影技术。为了更好地修剪搜索空间,该算法使用了基于重新定义的子树修剪策略。为了提高算法的性能,该算法提出了自我提升最小效用阈值的策略。实验结果表明,THN算法的性能明显优于对比算法,并且该算法在密集数据集中的表现尤其出色。但是,该算法在稀疏数据集的运行时间上效果较差。尽管THN算法在稀疏数据集上运行需要更长的时间,但其仍然是第一个挖掘含负项top-k高效用项集挖掘算法。最后,本文还对THN算法进行了可扩展性测试,结果表明该算法具有良好的可扩展性。 由于该算法在稀疏数据集上的表现不佳,未来的工作可以研究如何降低该算法在稀疏数据集上运行的时间。目前,含负项高效用项集挖掘算法较少,在下一步的工作中,我们可以研究在增量数据集和大数据中挖掘含负项高效用项集和挖掘精简的含负项高效用项集。
3 THN算法
3.1 数据集扫描技术





3.2 效用数组结构
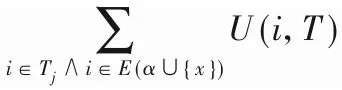
3.3 阈值提升策略
3.4 THN算法描述
3.5 THN算法示例

4 实验与结果分析

4.1 实验设计
4.2 执行时间性能
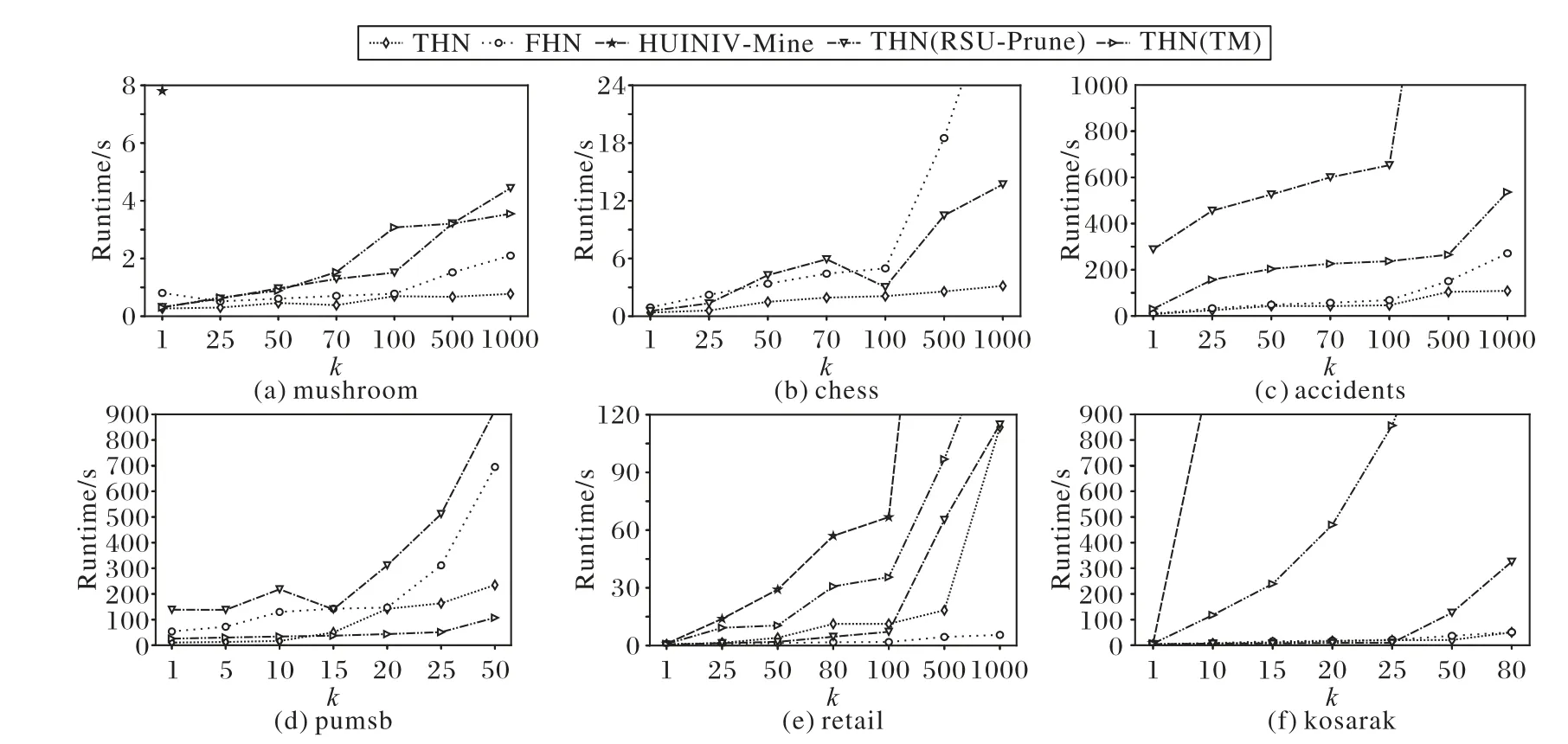
4.3 内存消耗性能

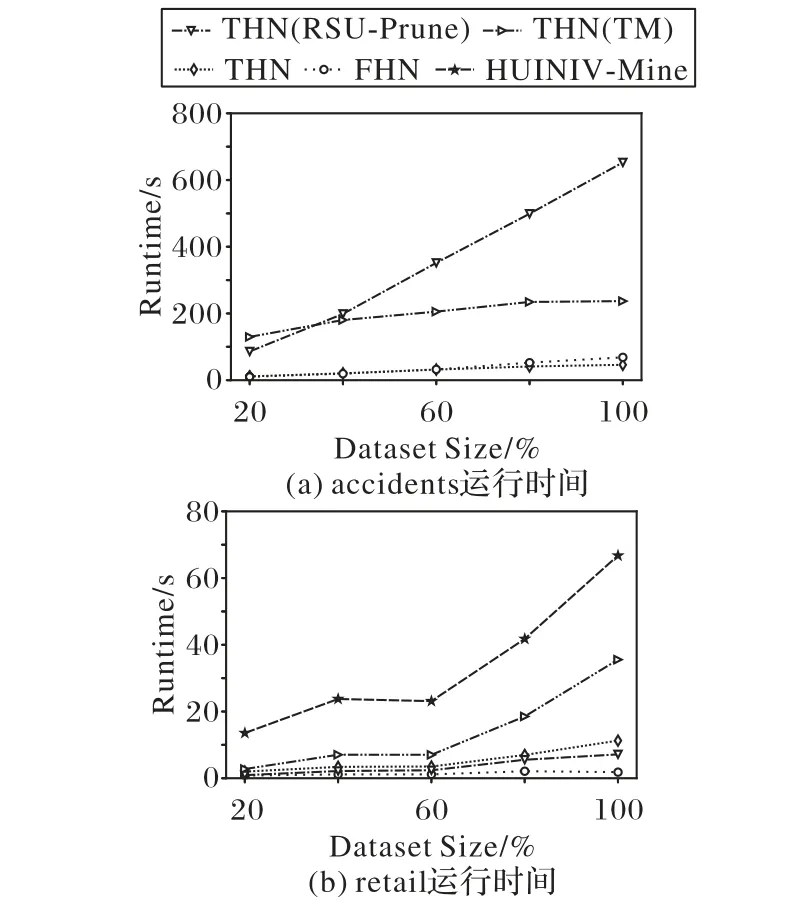
4.4 可扩展性

4.5 实验结论
5 结语

