基于人工蜂群与模糊C均值的自适应小波变换的噪声图像分割
石雪松,李宪华*,孙 青,宋 韬
(1.安徽理工大学机械工程学院,安徽淮南 232001;2.上海大学机电工程与自动化学院,上海 200444)
0 引言
图像分割是处理后续实际问题的基本预处理步骤,为初期图像处理和后期识别架起了桥梁。图像分割是将图片分割成目标和背景,目标如图像的突出区域、对象或对象的自然部分,其中分割过程是像素的分组过程,发生在邻域内具有相似属性的像素之间,如强度、颜色或纹理[1]。
噪声是计算机视觉处理中不可避免的一部分,如何避免噪声的影响是当前一个很有意义的研究方向。模糊C均值(Fuzzy C-means,FCM)算法是当前比较流行的图像分割方法,大量的研究人员对基于FCM算法的噪声图像分割方法展开了研究[2-6],相比于硬分割方法,FCM算法能保留更多的图像纹理细节信息。鉴于传统FCM算法的抗噪性能弱,相关学者提出将FCM算法与其他算法相结合的方法来去除噪声。文献[7]提出了一种基于模糊C均值与人工蜂群(Artificial Bee Colony,ABC)优化的灰度图像分割方法。文献[8-9]提出了粒子群优化(Particle Swarm Optimization,PSO)算法[10]与FCM结合的图像分割方法。PSO算法、遗传算法[10]、灰狼算法的引入在一定程度上提高了图像分割的鲁棒性。其中,PSO算法在搜索过程中容易陷入局部极值,且在进化后期阶段收敛精度较低、速度较慢[11]。目前也有研究人员通过改进FCM算法来增强算法的抗噪性能,文献[12]中提出一种边缘细分的动态参数模糊C均值图像分割算法,文献[13]中在目标函数中引入了局部和非局部信息,通过信息熵调整像素信息和非局部空间信息之间的权重,增强了算法的抗噪性能。以上分割方法较少地保留图像边缘纹理信息,仅在抗噪性能和分割性能上有所改进。
本文在基于传统的FCM图像分割的基础上提出一种基于小波变换的噪声图像FCM分割方法。首先,将噪声图像进行二维小波分解;其次,采用ABC算法对图像细节系数进行阈值处理,并对近似系数进行边缘增强;然后,使用FCM算法来进行图像分割,使其在分割时能更多地保留图像边缘纹理信息。
1 相关基础理论
1.1 小波变换
Mallat算法提出了多分辨分析的概念[14]。由于数字图像通常以二维数组f(x,y)来表示,假设二维信号为f(x,y),采用二维Mallat算法来进行小波变化,二维小波变换的定义为:

其中:a是引入的归一因子,保证了小波收缩前后能量不变;Ψ为傅里叶变换。
其逆变换为:

其中:

数字图像在经过二维小波分解后会得到4个分量,分别为对角系数D、水平系数H、垂直系数V和近似系数A,其中D、H和V又称之为细节系数。
1.2 小波阈值函数
本文采用软阈值函数[15-16]来对小波系数进行阈值处理,去除或衰减容易被噪声破坏的系数,保留有用的系数,从而抑制噪声,阈值函数为:

ABC算法以蜜源的形式来提供阈值,然后通过式(4)来对图像进行阈值处理。其中系数A并不进行阈值处理,因为A系数中包含很多对图像有用的细节信息。
1.3 自适应评估
每次迭代都要对蜜源性能进行评估,这样可以保证最终得到最优解。利用当前迭代的阈值系数进行阈值处理,处理后的细节系数和近似系数通过逆小波变换重建图像,然后根据重建图像计算FCM目标函数,如式(5)所示,其中数据点是每个像素点的灰度值。这种适应度评价直接针对分割结果,从而间接针对图像噪声。

虽然这个目标函数需要在ABC算法的每次迭代中进行计算,但是由于使用了基于直方图的FCM,总体计算成本在能够接受的范围内。
1.4 人工蜂群算法
ABC算法是模拟蜜蜂的觅食(采蜜)过程,组成要素有食物源、引领蜂、跟随蜂和侦察蜂[17]。


其中fi为解的函数值。
1)首先,初始化蜜源i的位置,按照式(7)在搜索空间中随机产生。
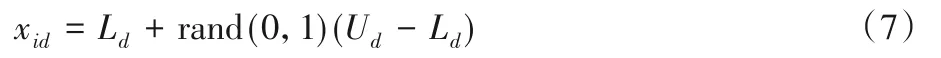
其中Ud和Ld分别为搜索空间的上边界和下边界。
2)更新蜜源位置。
在搜索之后,引领蜂根据式(8)在蜜源i周围搜索一个新的蜜源。

其中:j≠i,ϕ是在区间[-1,1]均匀分布的随机扰动系数。
3)跟随蜂按概率跟随引领蜂。
根据所获得的蜜源信息,并按式(9)来计算概率,按照概率来选择引领蜂跟随。

4)侦察蜂的产生。
设置迭代次数t,若蜜源i经过t次迭代后达到阈值界限threshold,但是并没有找到更好的蜜源,这种情况下蜜源i会被放弃,这时对应的采蜜蜂转变为侦查蜂,侦查蜂将继续在搜索空间继续搜索新的蜜源代替蜜源i。
1.5 边缘增强
图片在经过小波分解后,图片噪声存在于细节系数之中,为了保留图像边缘纹理特征,本文使用Canny边缘检测算法作用于近似系数之中来检测图像边缘信息,利用式(10)来实现图像增强,将这两个系数进行小波重构,保留了图像的边缘纹理特征,有效地提高图片的分割质量。

其中:k为[0,1]的常数,Ae为经过Canny边缘检测算法处理后的系数。
1.6 FCM
FCM算法是一种基于目标函数的模糊聚类算法,为了使得FCM分割速度更快,本文采用FCM对灰度级进行聚类,而不是对像素点进行聚类,这是因为一般情况下灰度级的数量要比像素点的数量小得多。利用聚类方式进行图像分割的实质是将灰度级集合分为C类的问题,每个类属中均含有唯一的聚类中心,在不断的迭代中实现聚类中心的更新,通过最小化目标函数优化聚类结果,使用隶属度矩阵来描述各个像素点的类属性质,通过单个像素点与聚类中心的相似程度来判断其在不同类别中的隶属程度。
图片中灰度级集合为X={x1,x2,…,xc},将这些数据划分为C类,那么聚类中心就有C个,xi是在一维向量空间中的一个与像素有关的特征向量,目标函数可改为:

其中:sj为灰度级为j的像素点数量;L为灰度级数量;m是隶属度因子,m∈(1,+∞);使用拉格朗日乘数得到聚类中心更新方程和使目标函数最小的隶属度方程。

2 基于小波变换的ABC算法的噪声图像分割
FCM算法直接对噪声图像进行分割,分割效果受到图像噪声严重影响,故本文先采用小波变换与ABC算法融合,降低图像噪声并增强图像边缘纹理信息,然后对重构后的图像进行FCM分割,使得分割后的图像鲁棒性更高。本文方法流程如图1所示。
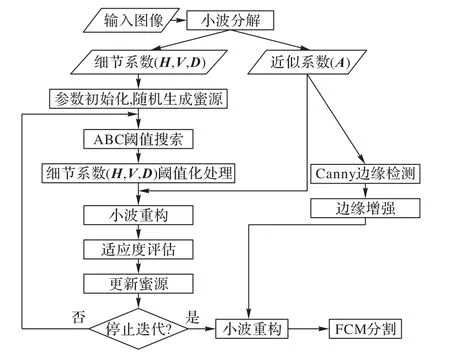
图1 本文方法流程Fig.1 Flow chart of proposed method
本文方法总体可分为四大步骤,如下所示:
步骤1 输入图像,将图像进行小波分解得到4个系数:

其中W表示小波分解。
步骤2 利用ABC算法对细节系数D、H和V分别进行阈值搜索,当适应度值不超过给定的阈值时,则在20次迭代后停止迭代,每次迭代后按当前阈值处理模糊系数,然后对模糊系数和未处理的细节系数进行小波重构,按照式(5)对重构后的图像进行评估,这样保证了获得最优阈值。

其中:ABC表示ABC算法搜索最优阈值;δ表示阈值;Th表示进行阈值处理。
步骤3 对模糊系数A进行边缘增强,具体表达式如式(10)所示。
步骤4 将处理后的系数进行小波重构,对重构后的图像进行FCM分割处理。

其中:W-1是小波逆变换,用来重构图像;FCM表示对图像进行FCM分割。
3 实验与结果分析
3.1 实验设计
为了验证本文方法的分割性能和噪声抑制能力,如图2所示,选取五张典型的灰度图像,分别命名为img1,img2,…,img5。并对这五张图像分别添加高斯噪声与椒盐噪声。首先对图像边缘增强中的系数k分别取0.5、0.7、0.9,然后对img1进行重构和分割,通过直接观察重构后和分割后的图像进行分析,从而选取合适的k值。然后聚类数C分别取3、5和6对img4进行分割实验,分析分类效果和目标函数收敛速度,选择合适的C值。最后分别采用本文的方法、传统的FCM方法和粒子群优化算法分割方法进行分割,得到三种不同的结果,然后采用峰值信噪比和误分率来定量地评价本文方法的抗噪性能和分割性能,采用算法运行时间来评价算法的时间复杂度。

图2 原图及添加噪声图像Fig.2 Original and noise added images
实验在Windows10系统下进行,CPU为AMD Ryzen 5 2600,主频3.40 GHz,运行内存为16 GB,实验环境是Matlab a2017版本下运行。
3.2 参数设计
在实验研究基础之上,ABC、FCM、小波变换、边缘增强相关参数如表1所示。

表1 关键参数设置Tab.1 Key parameter settings
3.3 结果与分析
图3是在不同k值下的图像重构与分割效果,直接观察可以发现在k取0.9时重构后的图像纹理最清晰,且分割后的效果最好。

图3 不同k值时图像重构效果和分割效果对比Fig.3 Comparison of image reconstruction effect and segmentation effect with different k values
图4是C值分别取3、5、6时FCM对img4含高斯噪声和椒盐噪声图像灰度值分类结果,发现当C取3时,图像灰度值所分类别区分度明显,C取5时,图像灰度值分类层次分明,在分割时能有利于保留一些纹理细节。

图4 C值取3、5、6时灰度值分类结果Fig.4 Classification results of grayscale valuewhen C value is3,5 and 6
图5是使用本文方法、FCM算法、PSO算法对这五张图片在添加不同噪声情况下进行分割后的结果,通过直接观察分割结果可以看出,本文算法分割后的图片受到噪声影响较小,特别是对含椒盐噪声图像分割上效果比其他两种方法有显著的提升,而本文算法在这两种噪声下保持一定的稳定性。

图5 分割后图像Fig.5 Segmented images
为了进一步验证本文方法的抗噪性能,本文采用峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)来定量地评价,PSNR越大,则表明本文方法抗噪性能越好,定义为:

其中,MAX为图像像素的最大值;MSE为图像像素均方差,定义为:

其中:m×n为图像的大小,K和I分别为原始含噪图像和分割后的图像。
为了进一步验证本文方法的分割性能,本文采用误分率(Misclassification Error,ME)作为指标来评价本文方法的分割性能,ME值越小,就表明本文方法分割性能越好,定义为:
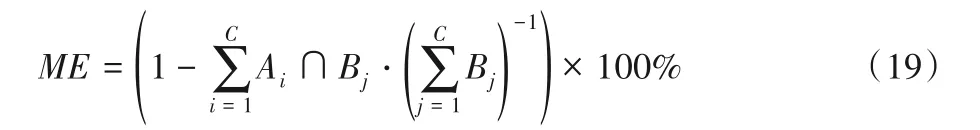
其中:Ai表示分割算法中分成第i类的像素点;Bj表示在没有噪声的理想图像中分成第j类的像素点;C为类别数。
为了客观地评价本文分割方法的抗噪性能与分割性能,表2给出了使用三种方法分割得到图像的PSNR值和ME值。

表2 三种方法对噪声图像分割后的PSNR,ME和所用时间Tab.2 PSNR,ME and time consumption of noisy image segmentation by three methods
对比分析这三种方法分割后图像的PSNR值和ME值,本文方法分割后图像PSNR值相较于传统FCM分割方法和PSO算法分割方法平均分别提升160%和20%,最多分别提升281%和54%;ME值平均分别降低28%和13%,最多分别降低55%和41%。本文方法对噪声图像的分割性能更好,并且具有更好的抗噪性能。但是对比算法运行时间,本文算法运行时间比传统FCM方法要长,与粒子群优化算法分割方法相比稍有优势。
4 结语
将噪声图像进行二维小波分解,然后采用ABC算法对图像细节系数进行阈值处理,并对近似系数进行边缘增强,最后使用FCM算法来进行图像分割。本文对五张不同的图像分别添加高斯噪声和椒盐噪声,然后对这些添加了噪声的图像分别使用本文方法、传统的FCM方法和PSO算法分割方法进行分割,将分割后图像的峰值信噪比和误分率作为性能指标,实验结果表明,本文方法能有效地保留图像的边缘特征,有较好的抗噪性能与分割性能。

