求解导数压轴题的零点效应与策略*
蒋满林
(福建省古田县第一中学, 352200)
新课标强调指出:高中数学以学生发展为本,培育科学精神和创新意识,提升数学学科核心素养,树立敢于质疑、善于思考、严谨求实态度,注重信息技术与数学课程的深度整合等[1].本文以2020全国卷I高考导数压轴题的解法为例,对如何引导学生进行自主解题与探索,在疑难中独立思考,在创新思维中应对问题,并在“端点效应”不适的基础上,提出了“零点效应”解题思路,以求于同行.
一、题目回顾
试题已知函数f(x)=ex+ax2-x.
(1)当a=1时,讨论f(x)的单调性;
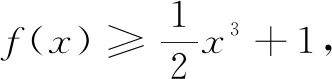
二、解法探析
第(1)问较易,这里只讨论第(2)问.
视角1字母讨论
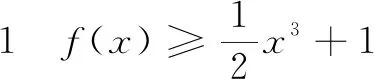
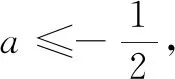
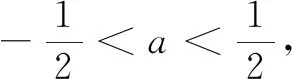
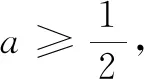
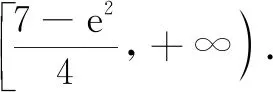
评注高考导数压轴题长期有“无讨论不压轴”的传统.求解含参的导数问题的通性通法是讨论,因此在标准解答中首选“讨论”解题策略,对落实四基、强化四能,培养数学核素养起到奠基的作用.
视角2分离参数
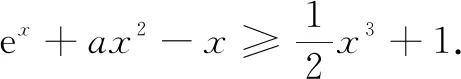
当x=0时,不等式显然成立.
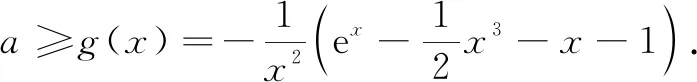
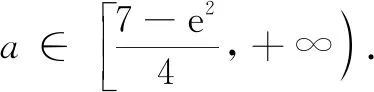
评注由于对字母讨论是学生的弱点,通常难以讨论完整,因此分离参数是师生处理此类问题的另一重要策略,使用此法常多于讨论法,在解题实践中能提升创新意识,找到更符合学生的“自然”解题思维.
视角3端点效应解题
再看网上盛传的“端点效应”的解答.
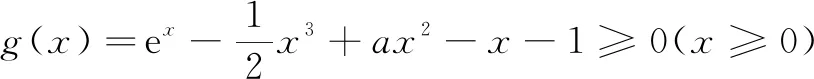
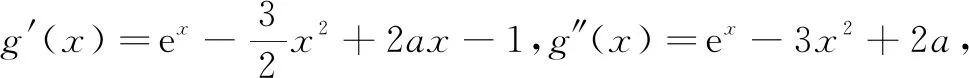
反思在导数含参数恒成立问题中屡建奇功的“端点效应”失灵了?难道是“端点效应”应用不对,还是 “端点效应”对这道函数题“水土不服”?
下面利用几何画板画出a取不同数值时的函数g(x)的图象如图1-3.


可见g(x)在(0,2)内随着a的取值不同,图象会出现凹凸反转,也就是函数在区间(0,+∞)有可能出现两个零点!而不是只有一个零点(限于中学内容,只研究函数有1个或2个零点的情形,以下同).鉴于往常使用端点效应的函数都只有一个零点,且端点就是零点,同时函数是恒单调的,因此由端点效应求出的必要性也就顺理成章成为充分性,导致解题时能屡试屡爽而不失灵,其实是图象的特殊性掩盖了“端点效应”解题的不严谨性.
对于有两个零点的函数,如何寻找第二个零点呢,或者说如何判断所求函数是一个零点还是两个零点呢?这是解决此类问题的关键.经过对函数图象的分析,我们可以判断函数的零点(区间端点除外)也往往是极值点,由此可用以下方法求得.
设g(x)的零点为x0.由
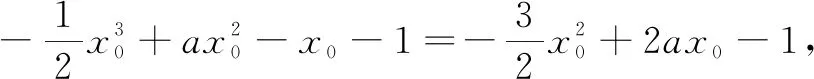
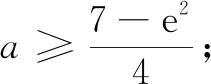
我们将上面的解题方法称为“零点效应”.可见端点效应是零点效应特殊情形,零点效应是端点效应的拓展;零点效应能够解决双零点问题,以及零点不在区间端点的含参导数恒成立问题.因此,在应用“零点效应”解题时,应该先找全函数的零点,再利用函数在零点处的函数与导数值非负(正),从而求出参数的取值范围.
评注从“端点效应”的不适进行探究,在信息技术的支持下探究新方法,寻找新思路,认识新技能,培养理性精神,创新思维活化思路,从而找到“零点效应”解题策略,并修正了“端点效应”的局限性,开拓了新的思维.
三、零点效应
现提出“零点效应”的解题模型与使用.
已知含参函数g(x),在区间[a,+∞)上g(x)≥0恒成立,求参数范围.
1. “零点效应”解题模型
第一步:求出函数的零点,即由g(x0)=0,g′(x0)=0解出x0(可能不只一个);
第二步:求出参数的取值范围,即由g(x0)=0,g′(x0)≥0或g(x0)=0,g′(x0)=0,g″(x0)≥0,或g(x0)≥0,g′(x0)≥0等求出参数的取值范围.
2.“零点效应”适用条件
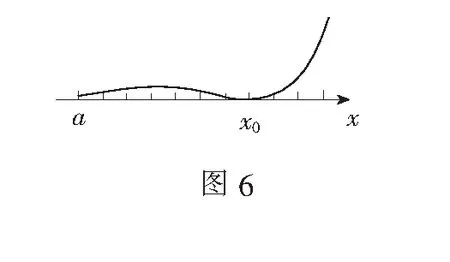
对于含参导数恒成立问题,所求函数只有一个零点或者有两个零点,并且函数值非负,如图4-6所示情形.

3.“零点效应”解题举例
例题(2020年山东高考题)已知函数f(x)=aex-1-lnx+lna.
(1)略;
(2)若f(x)≥1,求a的取值范围.
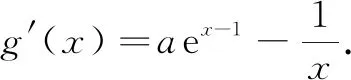
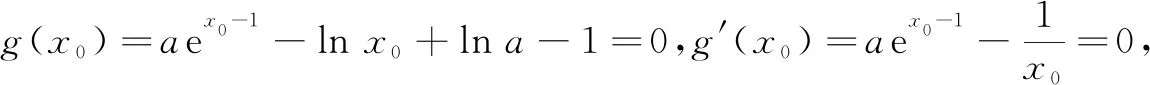
再由g(1)=a+lna-1≥0,g′(1)=a-1≥0,解得a≥1.

