动态管理模式下路侧停车泊位占有率预测方法

赵 聪，朱逸凡，李兴华，杜豫川

(同济大学道路与交通工程教育部重点实验室，上海201804)

0 引 言

我国城市规划对快速机动化背景下的停车供给和管理策略考虑不足，大中城市中心区均出现不同程度停车供需失衡现象，产生大量的停车巡游交通，进一步恶化城市交通拥堵状况.欧洲、美国等也曾面临同样的机动化和停车难问题，其通过改革停车管理政策实现需求管理，如时空差异定价、停车时长限制等；使用先进的技术手段盘活存量停车资源，如“互联网+停车”把碎片化的停车资源连接起来，打破信息孤岛.旧金山SFpark 项目，被ITDP(国际交通规划与发展政策研究所)称为“当前美国最具创新与最令人激动的拥堵管理工具”，是城市级停车管理的典型案例[1].通过路侧停车泊位咪表推断车位占用状态，根据局部区域占有率信息实现时空差异收费，并将车位占有信息、定价信息通过网站和APP 分享给用户.Pierce等[2]从需求角度分析旧金山停车定价模式，结果表明，停车用户的价格需求弹性平均值为-0.4，且价格需求弹性随时间、地点及其他因素大幅变化.

智能化停车管理手段提供了丰富的数据，通过数据驱动实现停车占有率有效预测，对提升动态管理政策的前瞻性和停车诱导系统的可靠性至关重要.单点停车场泊位占有率预测主要基于统计学和机器学习模型.季彦婕等[3]提出一种小波变换和粒子群小波神经网络组合的停车场占有率预测方法，与单独使用小波神经网络模型相比，预测精度提高了5～7 倍.陈海鹏等[4]采用小波变换与极限学习机(ELM)相结合的方法对短时空余停车泊位进行预测.向荣等[5]利用中心极限定理和大数定理对车位进行统计分析的基础上，结合长短期记忆网络(Long Short Term Memory,LSTM)对未来时段的停车位占有率进行有效预测.

现有研究主要有以下不足：①主要集中在单点区域的停车需求时间序列预测，缺少对空间关联的考虑，如一个停车场出现停车紧张现象，其周边一定范围内的停车设施都会受到相应影响；②现有智能技术可以有效实现动态化、精细化的停车管理模式，如果不考虑管理端的时空差异管理政策，仅从需求端的历史数据出发进行预测，难免造成较大误差.因此，本文将停车费率和车位时长约束两种动态管理模式信息作为输入，结合车位级的历史交易数据，形成大范围区域路侧停车泊位占有率和动态管理模式网格化图像，利用改进的卷积长短时记忆神经网络(Convolutional LSTM Network,ConvLSTM)[6]，综合卷积神经网络的空间特征提取能力和长短时记忆神经网络的时序特征提取能力，以美国旧金山为实例进行有效性验证.

1 数 据

1.1 旧金山路侧泊位交易数据

美国旧金山共有26 750个路侧停车泊位部署了智能咪表系统，按需实行浮动价格制.咪表费率调整幅度为0.25～7.75 美元/h，有些车位部分时间段免费，以街区为单位(约250 个街区)进行调整，目的是维持任何一个街区不超过80%的车位占有率.基于车位空置状况评估，调整停车时限，分为30，60，120 min 等不同的情况.收集2018年9～11月总计492万条交易数据，包括：车位编号，车位所在的街区，车位的经纬度坐标，订单起始时间，订单终止时间，订单支付费用等.整理每个车位的动态管理信息，包括日期，街区位置，车位编号，起始时间，终止时间，费率(美元/h)和时限(min)，数据格式如表1所示.

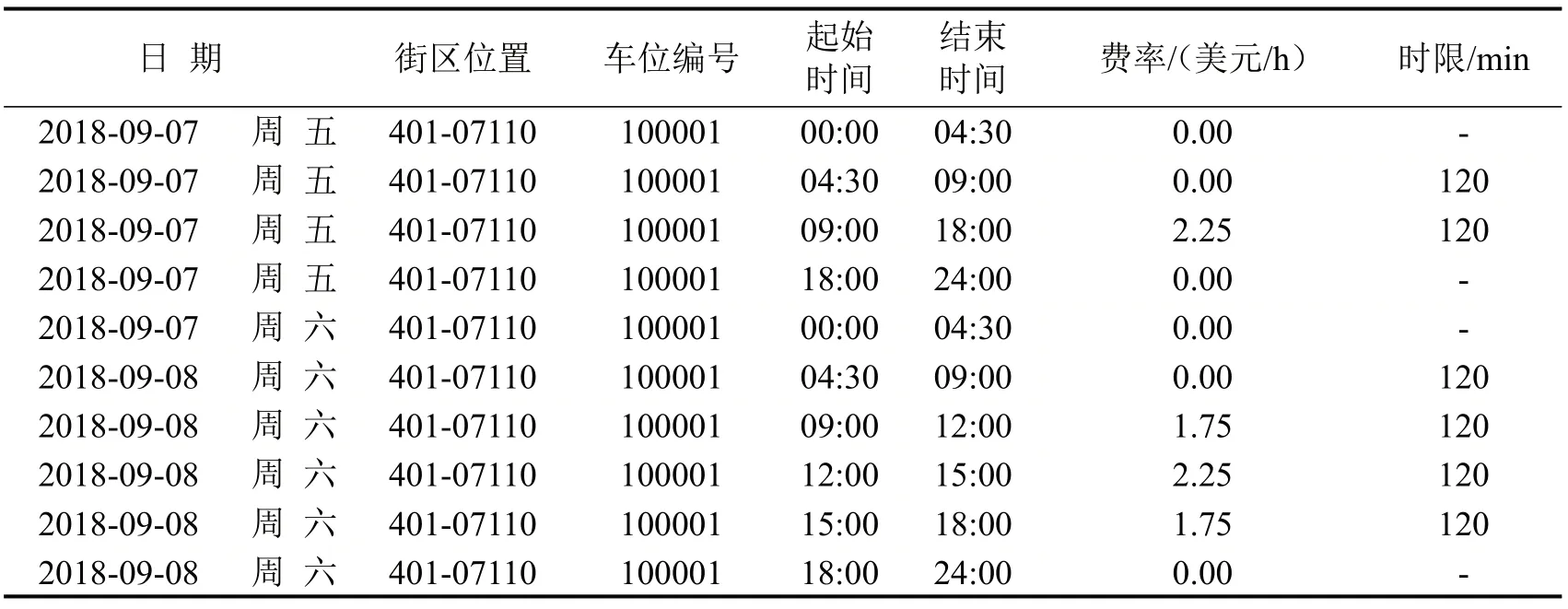
表1 数据格式Table 1 Data format

1.2 数据处理

将路侧泊位停车占有率预测问题转化为一个图像时间序列预测问题，对整个城市进行网格化集计处理，将其分为89×128 个网格，每个网格为100 m×100 m，保证每个网格内所有路侧泊位具有相对一致的动态管理政策及相似的供需特征.如图1所示，网格中的实心圆大小代表路侧泊位的数量级，最大值为120，最小值为0.

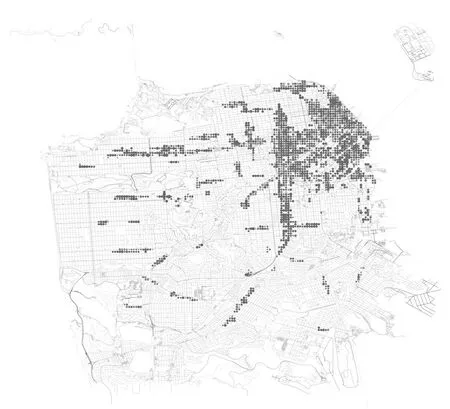
图1 车位数量分布图Fig.1 Number of parking spots in each cell of the city

对每个网格内的路侧泊位数据做集计化处理，得到3 个网格化的数据矩阵，分别为网格的平均泊位占有率、平均停车费率和平均停车时限，计算公式如下.

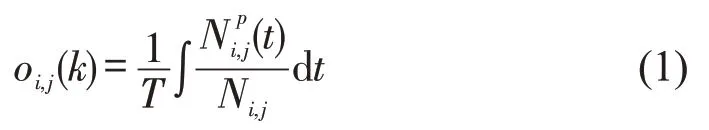
式中：i，j为网格所在位置；T为时间步长，由于停车管理政策变化是以30 min 为单位，故本文将时间步长取为30 min；oi,j(k)为网格在第k时间段的平均路侧泊位占有率，为网格在t时刻被占用的车位数量；Ni,j为网格的车位总数.

式中：fi,j(k)为网格在第k时间段的平均停车费率，为网格内的车位a在t时刻停车费率；fmax为最大停车费率，即7.75美元/h.

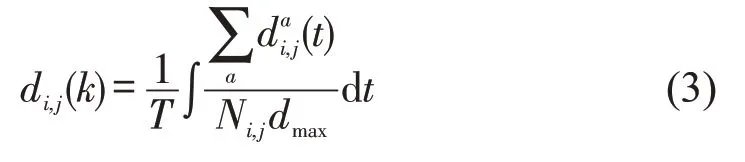
式中：di,j(k)为网格在第k时间段的平均停车时限；为网格内车位a在t时刻停车时限；dmax为最大停车时限，这里取1 d，即1 440 min.当车位无停车时限时，di,j(k)=1 ；当车位为专用车位时，di,j(k)=0.

2 预测模型

2.1 ConvLSTM网络模型

LSTM 是Hochreiter 等[7]提出的一种特殊的循环神经网络(Recurrent Neural Network，RNN)，在隐藏层中增加记忆单元，具有长短时记忆机制，解决一般RNN 存在的长期依赖不足问题；有效解决传统RNN随网络层数增加而出现梯度消失或梯度爆炸等问题，非常适用于与时间序列相关的预测问题，包括单体停车场泊位占有率预测[6]等.LSTM在单元结构中使用记忆单元控制信息流，引入输入门、遗忘门和输出门调节信息流，让网络对历史信息的保留和遗忘更有选择性，避免梯度消失和梯度爆炸问题.遗忘门用于决定上一神经元信息的遗忘程度，避免无效信息对当前神经元状态的干扰，它查看前一步神经元输入和当前步神经元输入，输出[0,1]之间的数值，1 表示完全保留，0 表示完全遗忘；输入门通过上一步中的隐层状态和本步骤的输入计算神经元的更新信息，然后交给tanh 激活函数将数值范围压缩到(-1,1)，用于更新本步骤中的神经元状态；输出门则将本步骤的神经元状态通过tanh 进行激活，经过sigmoid进行筛选过滤后，作为本次隐层输出状态，交给下一步神经元.

LSTM对时序数据的处理较有优势，但对本文构建的网格化停车数据，无法学习到每个点和周围点的空间相关性，难以提取空间特征.因此，本文应用ConvLSTM 结构，在LSTM 的基础上增加卷积计算提取空间特征.两者相比，经典的LSTM状态间采用全连接形式，而ConvLSTM 采用卷积形式.

基于所划分区域网格数量，网络结构如图2所示.数据输入后：首先经过三层连续ConvLSTM层，逐步提取数据中的时间特征和空间特征，每层ConvLSTM 卷积核大小均为3×3，所包含的ConvLSTM 卷积核数量分别为16、32 和64 个；随后，连接两层全连接层，控制后一个全连接层的单元数与网格总数相等；最后，连接Reshape层，输出与输入数据相同尺寸的矩阵作为预测结果.以上所有隐含层的激活函数均为ReLU函数，结构中每个ConvLSTM 层都进行批归一化处理，使每一层结果在经过激活函数前归一化，有效提高网络的训练速度，防止模型过拟合.

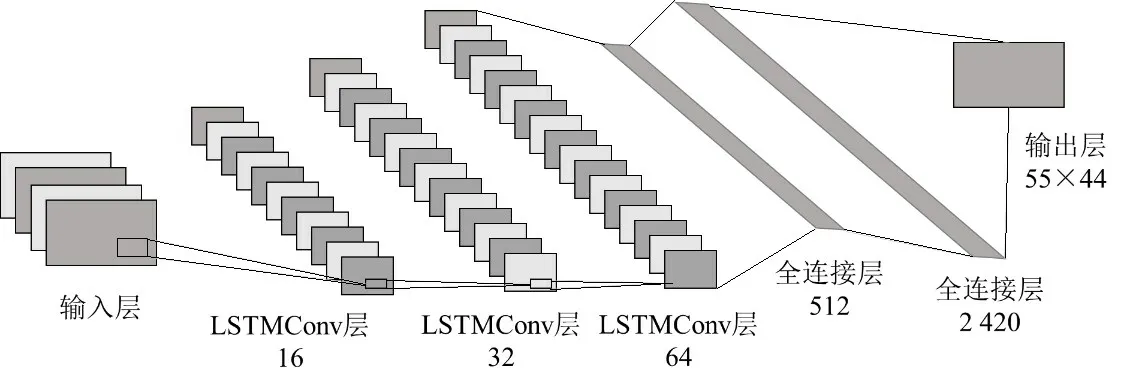
图2 网络结构示意图Fig.2 Network structure diagram

2.2 无政策模型与有政策模型

为分析动态管理模式下政策信息对模型预测效果的影响，在ConvLSTM 网络基础上分别构建有政策数据输入和无政策数据输入模型.为便于描述，将仅用网格泊位占有率数据训练的神经网络称为“无政策模型”，加入网格动态费率和停车时限动态政策数据的称为“有政策模型”.

结合1.2节数据处理，定义3个矩阵为

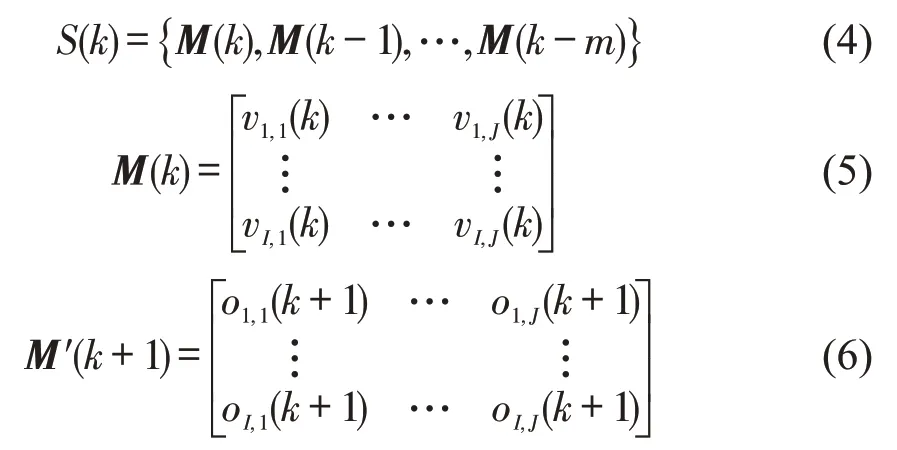
式中：S(k)为第k时间段预测所输入的前序数据集；m为前序时间段数量，由于路侧车位停车时长以短时停车为主(2 h以内)，故本文中取m=3；M(k)为整个区域的空间网格矩阵；I,J代表行列数，分别为89 和128；M′(k+1)为预测模型输出信息，即下一时间段每个网格的路侧泊位平均占有率.

无政策模型的网格数据输入信息为

式中：vi,j(k)为该网格内所包含的平均泊位占有率单个通道信息.

有政策模型的网格数据输入信息为

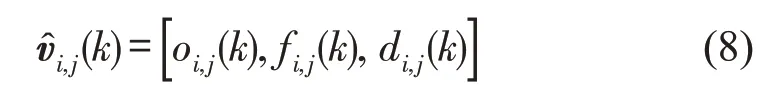
式中：为该网格内所包含的平均泊位占有率、平均停车费率和平均停车时限3个通道信息.

3 模型训练与结果分析

3.1 网络模型训练

训练参数，即模型超参数的设置会对训练结果产生较大影响.结合搭建网络模型特点，反复试错，最终选择训练参数如表2 所示.模型的损失函数选择平均方误差MSE，重点考虑差的大小而不考虑其方向，给与较大的差值更大的处罚.Adam优化器可在训练中自适应调整学习率，提高训练效率和精度.学习率影响模型的初始学习速度，批大小影响模型跳出局部最优点的能力和收敛速度，经过试验，分别取0.000 3和32.

表2 训练参数Table 2 Values of hyperparameters

无政策模型和有政策模型训练参数一致，网络性能随训练周期的变化如图3 所示.由图3 可知：加入政策数据(虚线)之后，网络训练速度和最终性能均有明显提升；有政策模型约在第50 个训练周期达到稳定，相比无政策模型，其主要评价指标的测试集均方误差从0.001 7下降到了0.001 4.

3.2 预测结果分析

随机抽取一帧样例数据(旧金山中午12:00 的路侧泊位占有率情况，绝大多数区域均有车辆停放，便于效果对比)，输入到训练好的两种模型中进行预测，结果如图4所示.可发现，无政策模型和有政策模型均能较好地得到未来时间段的泊位占有率.两者相比，无政策模型的预测结果值整体更加接近，在图像上表现为图像亮度更加平均；有政策模型则更好的预测出相邻区域间的差异性，在图像上表现为图像亮度更加尖锐.

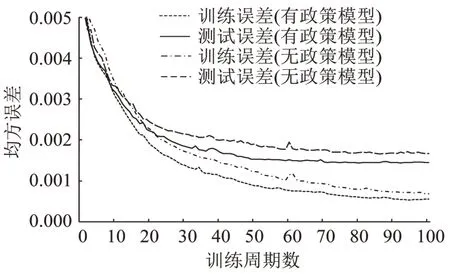
图3 网络训练结果Fig.3 Network training results

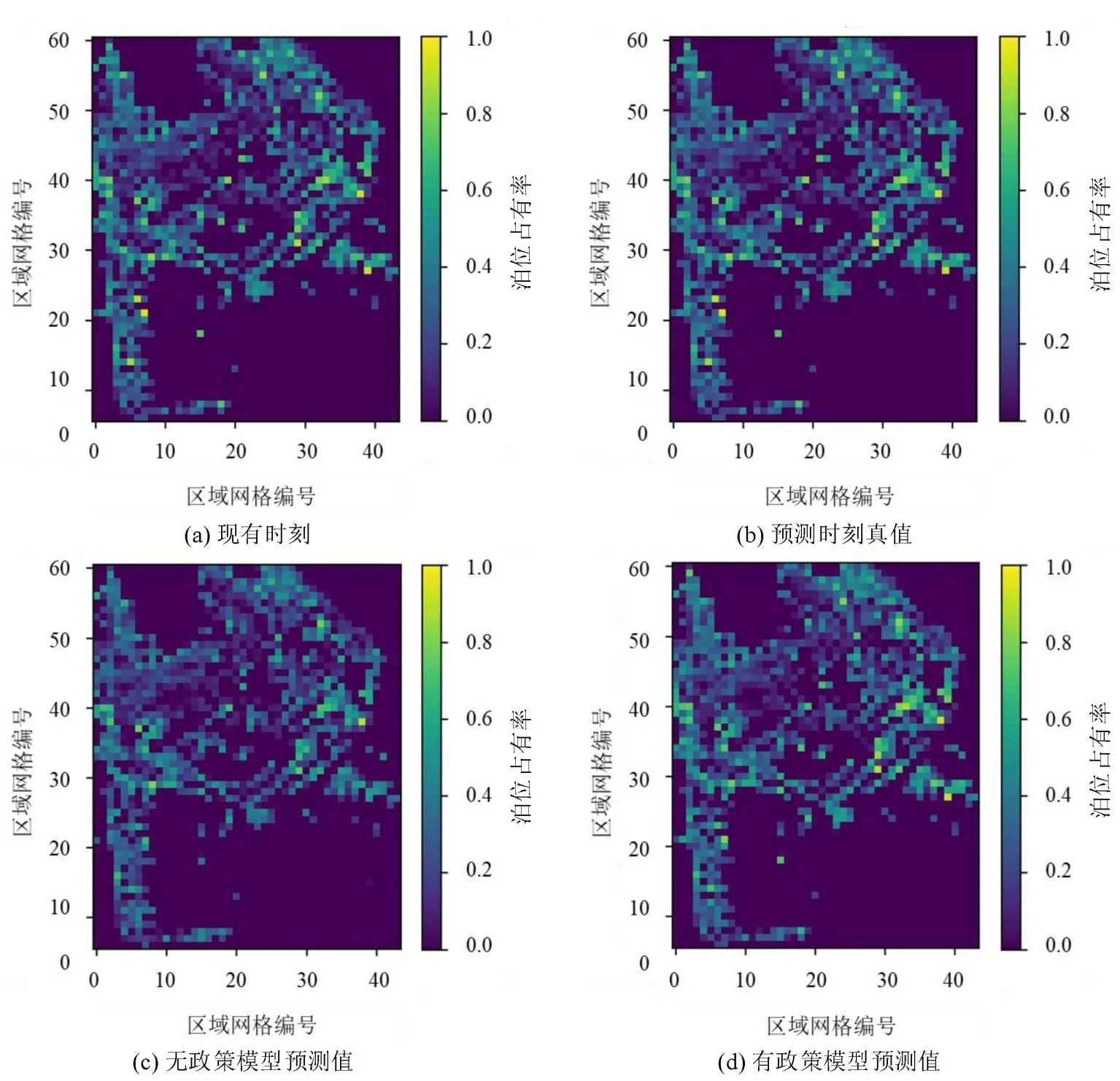
图4 真值与模型预测结果Fig.4 Ground truth and model prediction

定量分析两种模型的预测结果，定义每个网格的相对预测误差为

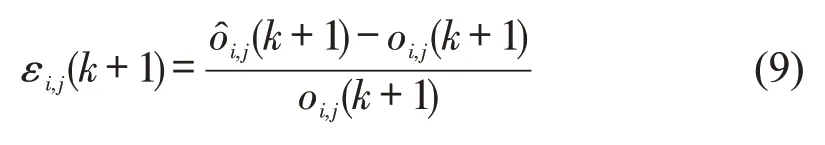
式中：εi,j(k+1)为网格(i,j)在k+1 时刻的相对预测误差；为网格的泊位占有率预测值；oi,j(k+1)为该网格泊位占有率在预测时刻的真值.

图5为两模型的预测误差分布直方图，其中，0表示预测值与真值相同，-1或1表示预测值低于或高于真值1 倍.由图5 可知：无政策模型的相对预测误差较为分散，有政策模型的相对预测误差向0集中；无政策模型和有政策模型的平均相对预测误差绝对值分别为0.324 2，0.213 9，可见有政策模型的预测精度优于无政策模型.

图5 网格模型预测相对误差分布直方图Fig.5 Distribution histogram of model prediction errors for all cells

为更好地观察两种预测模型的周期性特征与预测能力差别，按周将连续8周的预测误差结果作均值处理，如图6 所示.由图6 可知：周日，两个模型的预测误差均较小；周一～周六，有政策模型的预测能力明显优于无政策模型.进而，将周一～周六的模型预测误差再次作均值处理，如图7 所示.可知，有政策模型优于无政策模型，且无政策模型在18:00出现非常大的预测误差.结合旧金山市的停车政策可知，工作日和周六的18:00将很多车位从收费有停车时限变为免费无停车时限.

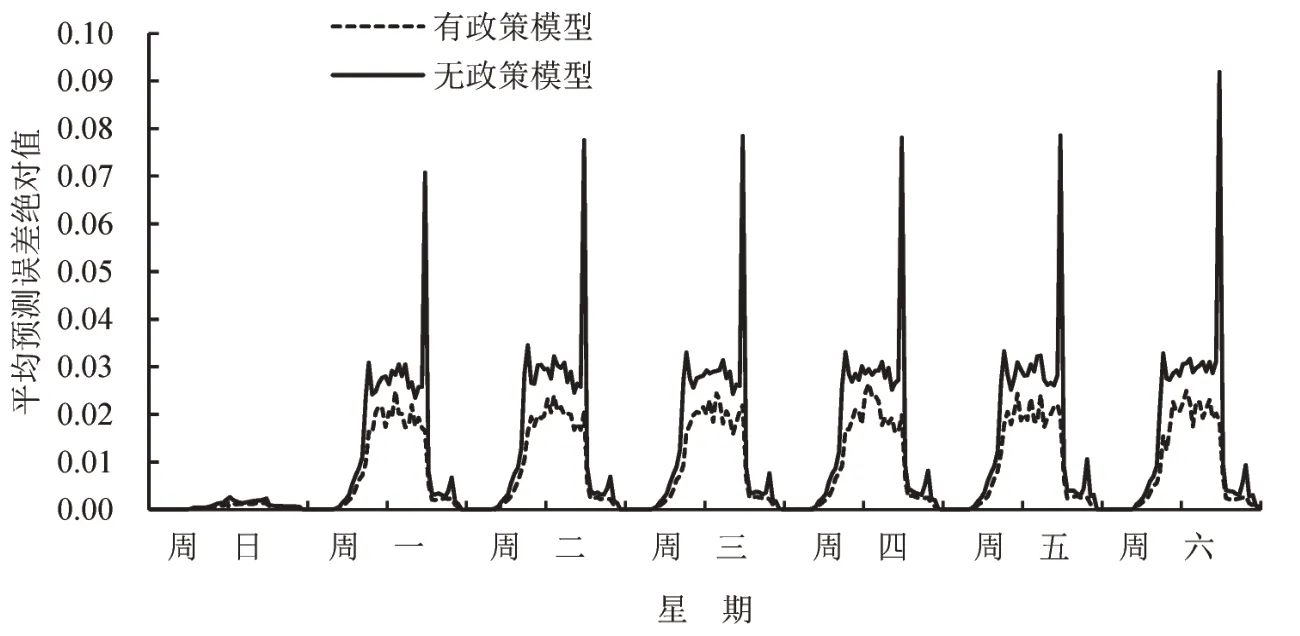
图6 按周平均的模型预测误差Fig.6 Model prediction error by weekly average

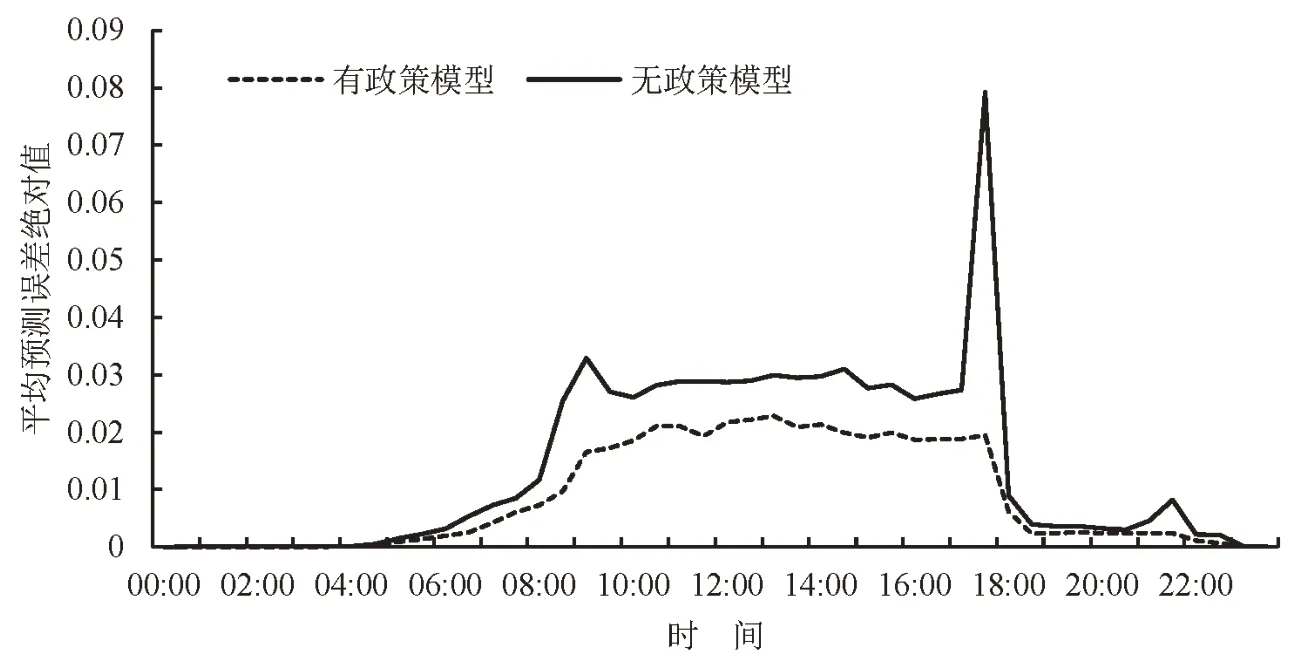
图7 按周平均的模型预测误差(除周日外)Fig.7 Model prediction error by daily average(except Sunday)

两种模型预测误差在一周中不同天和一天中不同时间的变化不同，结合Pierce等[2]的研究结论，用户的停车行为会受到动态定价等因素的影响，且在城市的不同区位，一周中不同天和一天中不同时刻的价格需求弹性是不同的.有政策模型在数据训练阶段可以在动态政策与泊位占有率对应变化中学习用户分区分时间的行为特征信息，进而在预测阶段，结合动态政策可以更精准的预测泊位占有率变化；在政策变化与用户停车行为关系解析上，无政策模型因无对应的学习数据，在政策变化阶段将造成较大的预测误差.

4 结 论

本文针对动态管理模式下城市路侧停车泊位占有率预测问题，将城市网格化的基础上，利用ConvLSTM 结构的深度神经网络提取泊位占有率数据的时间特征和空间特征，分别训练融合动态费率和动态停车时限两种管理政策的有政策模型，和无动态管理政策输入的无政策模型.结果显示，在大部分时段两种模型均能够有效地预测下一时段的泊位平均占有率，但有政策模型相较于无政策模型，训练效率和预测精度得到显著提升，预测平均方误差减小到0.001 4.同时，由于无政策模型无法学习到政策变化与用户停车行为变化的时空对应关系，在停车管理政策发生突变时段，无政策模型的预测误差会陡增；有政策模型预测结果比较平滑，误差较小.在动态化、精细化的城市停车管理模式下，本文提出的路侧泊位占有率预测方法可以为政策调整和停车诱导提供有效信息.