停车许可证的动态最优供给策略

王鹏飞，王安格，关宏志，赵 磊,3，赵鹏飞

(1.北京工业大学a.城市与工程安全减灾教育部重点实验室，b.城市建设学部，北京100124；2.河北科技师范学院城市建设学院，河北秦皇岛066004；3.北京易华录信息技术股份有限公司，北京100043；4.北京建筑大学土木与交通工程学院，北京102616)

0 引 言

根据《2019 北京市交通发展年度报告》，截止2018年底，北京市机动车保有量约为608.4 万辆，而备案停车位仅有189.1万个，缺口超过68.9%.为此，交通学者针对交通需求管理中的停车预约系统与停车许可证展开了大量研究.

Shao等[1]考虑居住区泊位使用特征，引入预约机制构建泊位共享场景下系统效益最大化模型；Xiao 等[2]基于拍卖理论提出共享泊位资源最优分配—定价机制；Wang 等[3]以停车许可证为手段构建公共泊位最优分配—定价机制，并在此基础上制定不可预约公共泊位动态定价机制；Wang 等[4]分别以最小化总出行成本和尾气排放量为目标，构建停车许可证最优供给机制；王鹏飞等[5]基于拍卖机制构建路外公共泊位资源最优定价模型.

相较传统停车预约和预定价机制，停车许可证既可以实现泊位预约，又可以不依赖用户停车需求函数预测实现精准的有限停车资源最优分配—定价和社会福利最大化的明显优势[3].上述停车许可证机制设计从实际应用角度仍存在以下不足：①除文献[3]外，鲜有将可预约与不可预约停车设施同时考虑，而文献[3]中用户对两种停车设施的选择是外生给定的，没有讨论最优供给机制；②多数研究中制定动态泊位分配机制是基于对未来停车需求的预测，鲜有对泊位动态供给机制进行探讨，但管理者与用户之间存在信息非对称会使预测结果偏离现实；③并非全部持有停车许可证的用户都能够按照预约时间到达或离开泊位，特别是比预约时间早到达、晚离开泊位的用户，是造成停车设施入口处车辆排队等待的重要原因.鉴于此，在考虑持有停车许可证用户行为不确定性的基础上，本文制定一种基于实时观测数据的停车许可证的最优动态供给策略，以实现所有用户时间损失期望值最小化，此机制也是实现公共泊位最优动态定价的基础.

1 场景设定

1.1 停车设施与停车许可证

停车许可证(或停车预约系统)的作用是使一部分用户在出行前即可预定泊位，进而减少寻泊交通量和时间损失.现实中，并非所有公共泊位都是可预约的，即可预约和不可预约公共停车设施往往共存于一个区域，其管理者均为政府.对于可预约停车设施，政府的管理手段为停车许可证.停车许可证是一种在指定时间段内在指定停车设施才可以泊车的权利，由泊位管理平台(政府)进行分配和定价，未持有停车许可证的用户不能在指定的停车设施泊车.本文在动态框架下进行，以时刻t为开始停车时间的停车许可证只在时刻t-Δt进行预定购买，此处的Δt为单位停车时长.在此设定下，停车许可证在线发行，政府可以通过拍卖[2-3]实现公共停车资源的动态供给、分配、定价.由于泊位资源有限，并非所有参与预定购买的用户最终都可以获得停车许可证，未获得停车许可证的用户只能通过巡航去寻找不可预约停车设施的空余泊位，即寻泊.

1.2 停车许可证用户及其行为的不确定性

现实中，部分持有停车许可证的用户会出现比预约时间早到或晚离开停车设施的偶发性行为，这会使停车设施入口处产生车辆排队等待空余泊位的现象.为遏制这种不良现象，管理者制定停车许可证的最优动态供给策略，以最小化停车许可证用户的排队时间和未持有停车许可证用户寻泊时间的总和.同时，停车许可证的供给量确定后，通过现有的拍卖机制[3]即可实现停车许可证的动态分配—定价.

2 模型构建

2.1 时间损失

设T为固定的终端时刻，在[0,T]期间，系统总时间损失Ψ定义为

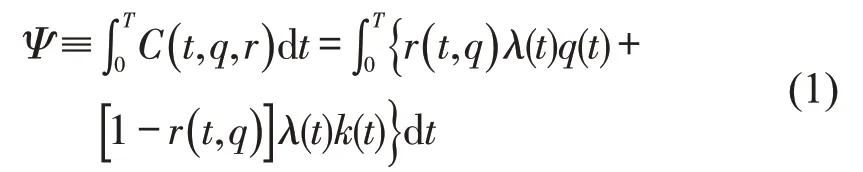
式中：C(t,q,r)为系统在时刻t的时间损失；λ(t)为时刻t参加停车许可证拍卖的人数，亦为(可实时观测到的)停车需求；q(t)为时刻t用户在停车设施入口处的排队时间；k(t)为时刻t区域内所有寻泊用户的平均寻泊时间；r(t,q)为时刻t总停车需求中获得停车许可证用户的比例，是本模型的控制参数；k(t)为时变且外生给定的参数；q(t)为系统的状态变量.

根据1.2 节场景设定，状态变量q(t)应符合演变规律：排队长度既受r(t,q) 的控制，又存在不确定性，且不确定性随停车需求中获得停车许可证用户数量r(t,q)λ(t)的增加而增加，即

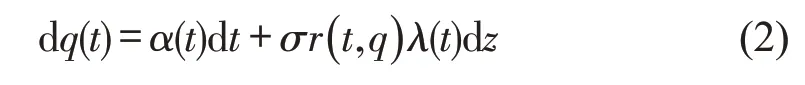
式中：σ为干扰项，可视作随机变量的标准差；z为标准维纳过程；α(t)是期望项，表示在微小时间段dt内排队时间变化的期望值，根据是否存在排队时间q(t)分为两种情况，即

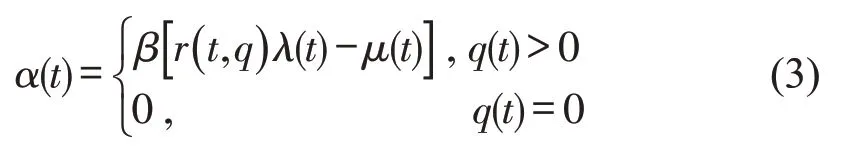
式中：β为排队长度与排队时间之间的换算系数；μ(t)为时刻t剩余泊位数量.

2.2 动态系统最优

由于持有停车许可证用户的行为存在不确定性，定义动态系统最优问题(DSO)，最小化系统总时间损失的期望值，即

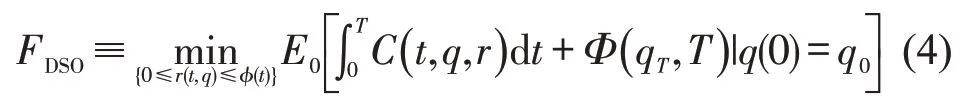
式中：q0，qT分别为系统初始t=0 和结束t=T时的排队时间；Φ(qT,T)为自由的终端状态；φ(t)为控制参数r(t,q)的上限，φ(t)=min{μ(t)/λ(t),1}，因为停车需求可能超过可预约空余泊位数量；E0为系统在[0,T]期间的时间损失期望值；FDSO为[0,T]期间系统总时间损失的最小化期望值.

2.3 最优性条件

为求解动态系统最优问题(DSO)，利用动态规划原理分析最优性条件：哈密尔顿-雅克比-贝尔曼(Hamilton-Jacobi-Bellman Equation，HJB)方程.定义最优值函数V(·) ，因函数已经取得最优值，故其只和状态变量有关，与控制变量无关.

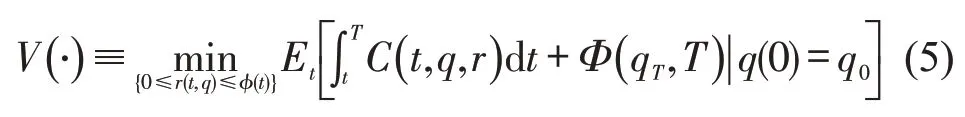
此处，Et为系统在[t,T] 期间的时间损失期望值.对式(5)应用动态规划原理，可得

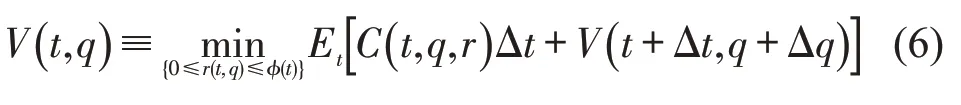
对式(6)中V(t+Δt,q+Δq)进行泰勒展开，忽略高次项可得式(7).此外，为简化表达，以下所有公式省略(t,q,r)、(t,q)和(t).

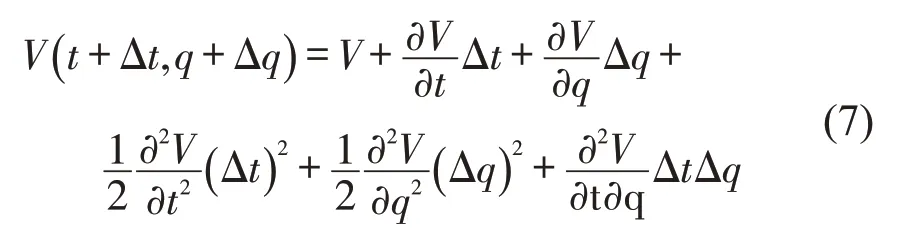
z为标准维纳过程，可得

将式(8)带入式(2)，可得

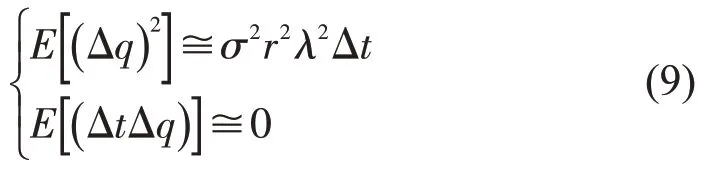
将式(2)等价变化为

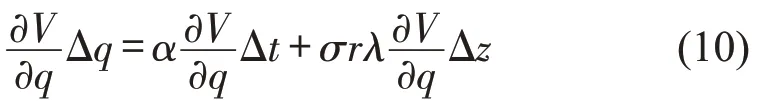
再将式(9)和式(10)代入式(7)可得

最后，将式(11)代入式(6)，等式两端同时消除Δt，可得HJB方程为

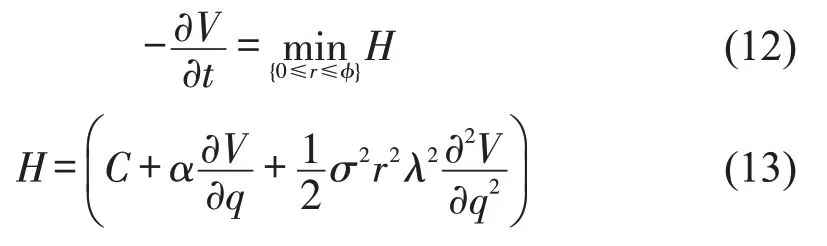
HJB 方程的意义是寻找最优供给策略r*，使微小时间段dt内最优值函数的变化值最小.式(13)等号右边第1项为系统总时间损失，第2项为排队时间的微小变化对系统总时间损失的影响，第3项为不可控因素对系统总时间损失造成的影响.

2.4 带有偏导数项的最优供给策略

根据式(2)和式(3)可知，期望项α是根据有无排队时间q进行计算的，故HJB 方程可分为两种情况进行探讨：q ＞0(用下角标“+”表示)和q=0(用下角标“0”表示).

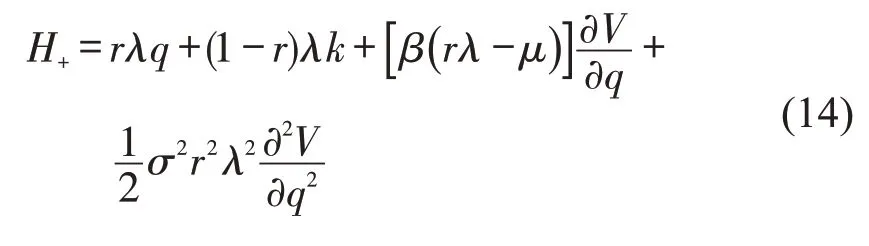
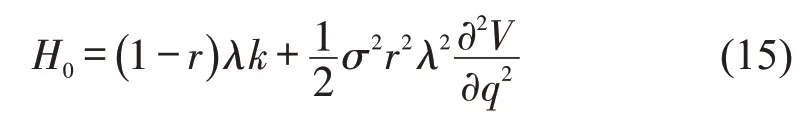
求解最优供给策略r*，则考虑使用式(14)和式(15)对r求导.分别在q ＞0 和q=0 的情况下得到的最优供给策略.

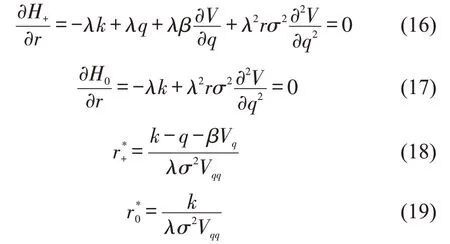
3 求解方法

3.1 最优值函数的设定

由式(18)和式(19)可知：若管理者可明确掌握最优值函数V的形式，则可直接求解得到不含偏导数项的最优供给策略r*；否则，将无法计算.文献[6]提出基于广义线性互补理论的求解方法，但此方法需要控制策略为Bang-Bang形，无法适用于本文.在机器学习领域，利用值函数近似理论也可以对最优值函数的形式进行确定，但这需要对最优值函数的形式进行预先设定，同时对环境变换的适应能力也比较差.

现实中，管理者通过长期观测可大体把握最优值函数的形式，但其中的具体参数还需要单独求解.故采用提前预设值函数后求解其中参数的方法[7].

式中：VA为预设值函数，其仅与状态变量q有关，与供给策略r无关；s为待估参数.

3.2 最优动态供给策略的解析解

将最优供给策略分别代入HJB 方程，可以消除其中最小化“min”，因为代入之后即为最优.将预设值函数VA带入HJB方程中，即可得到待估参数s为

4 数值实验

4.1 数值设定

以北京市国贸地区为例进行数值实验，实地调研后的参数设定如表1所示.07:00-21:00的总停车需求为42 724 veh，实时停车需求如图1所示.每个时刻到达可预约停车设施的用户停车时长是随机设置的，平均寻泊时间为5 min[8].

4.2 结果分析

在4.1节数值设定下，由图2典型案例可知：

(1)相比无停车预约系统(方形)，停车许可证的完全供给策略(三角形)可大幅降低早高峰时段的寻泊交通总量及时间损失，全天降低时间损失约1.33 min/veh；

表1 数值设定Table 1 Numerical settings

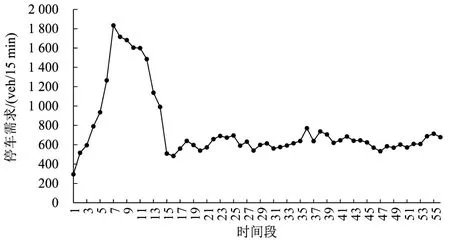
图1 停车需求时变图(07:00-21:00)Fig.1 Time-series of parking demand(07:00-21:00)

(2)相比完全供给策略，最优供给策略(圆点)全天可节约时间约0.63 min/veh，证明了最优供给策略的优越性；

(3)最优供给策略经常在泊位供给领域的两个端点附近取值且反复跳跃，这与控制理论中使系统消耗最低的Bang-Bang控制策略相似；

(4)无停车预约系统下的时间损失为5 min/veh，与文献[8]的实际调研结果一致，据此可验证实验结果的正确性.

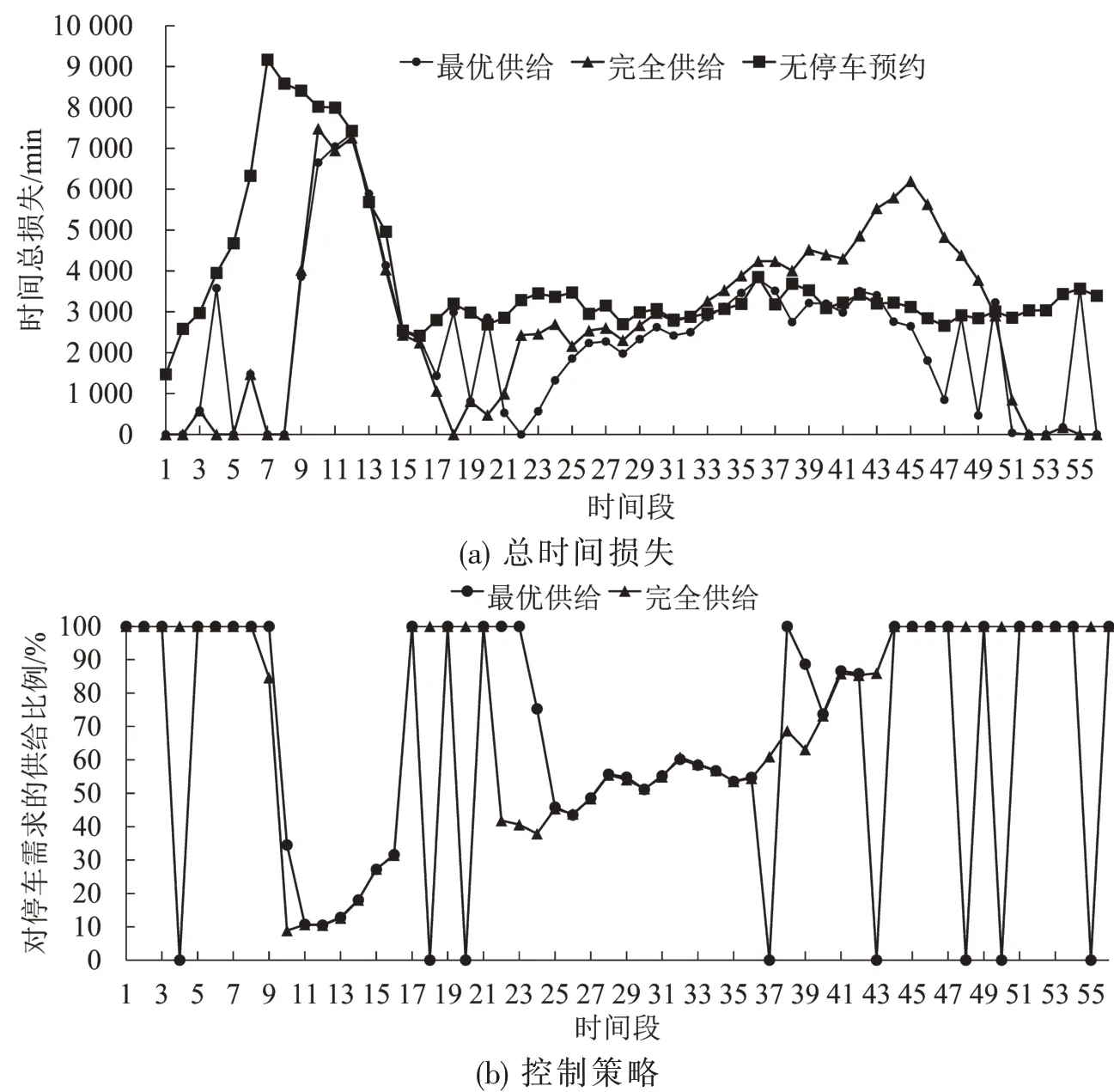
图2 不同控制策略的比较(典型案例，σ=0.1)Fig.2 Comparison of different control strategies(Typical example,σ=0.1)

为验证典型案例得到的最优供给策略降低时间损失的鲁棒性，在不同的停车许可证用户行为不确定性水平下，分别进行10 000 次的蒙特卡洛实验，结果如表2所示.

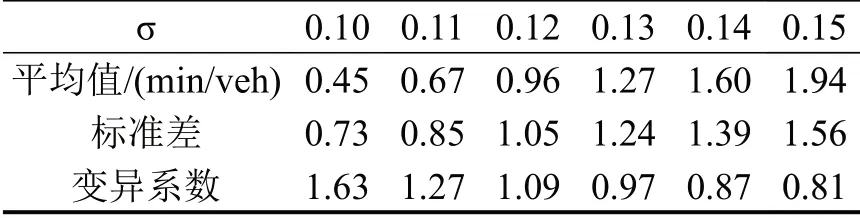
表2 在不同的停车许可证用户行为不确定性条件下的蒙特卡洛实验结果Table 2 Monte-Carlo experiment results under different σ

由表2可知：①随着不确定性水平的增加，相较完全供给策略，最优供给策略所能节约的时间平均值逐渐增加，变异系数逐渐减小，这意味着不确定性水平越高，最优供给策略的优势越明显，发挥越稳定.②在不确定性较小时，有可能在一次独立实验中出现最优供给策略并非最优结果，这可能是因为管理者仅能把握随机变量q的特征值，即期望值与标准差，并不知道下一时刻的真实状况，还可能与最优值函数的预设形式有关.

5 结 论

本文以可预约和不可预约公共停车设施共存的区域为对象，从理论上得到系统总时间损失期望值最小化的停车许可证动态最优供给策略，并通过数值实验验证了策略的有效性.所得结论如下：动态最优供给策略是车辆排队时间的函数，并根据排队时间是否存在分为两种情况；相较停车许可证完全供给策略，动态最优供给策略可显著节约用户的出行时间；随着停车许可证用户行为不确定性的增加，动态最优供给策略平均节约时间增加，变异系数下降.

与既有研究成果相比：本文策略实现了停车许可证的动态供给，对文献[4]停车许可证最优静态供给策略方面的研究进行了补充；在本文成果的基础上，利用拍卖机制[3]即可实现停车许可证的动态最优定价；与停车许可证的多时间点交易市场机制[9]相比，本文策略无需逐日迭代计算即可实现系统总时间损失期望值最小化.