基于多旅行商问题的应急设施服务区划分模型
赵 星,吉 康,申 珂
(河海大学土木与交通学院,南京210098)
0 引 言
近年来,全球范围内各类突发公共卫生事件频繁发生,例如,2002年SARS 事件,2019年新型冠状病毒事件.面对此类区域性的突发公共卫生事件,疫区的应急设施服务区划分,例如临时医院,物资周转中心,避难所等,可以帮助物资配送及紧急救援,是控制疫情发展,保障民众生活需要的基本前提.
应急设施位置选择对服务区域划分具有重要影响,较多研究将应急设施选址问题与服务区域划分问题联合求解.典型选址—分配(Location-Allocation,L-A)模型根据其优化目标不同可以分为:P-中值模型,P-中心模型,覆盖模型,均已有成熟的研究应用[1].Pan[2]以各个疏散集结点到避难所的加权距离和最小为优化目标,构建了一种基于P-中值问题的避难所选址—分配模型,采用遗传算法进行求解,可同步获得避难所最优选址与服务区划分方案.郭鹏辉等[3]研究了灾后救援物资选址—路径—配给的集成优化问题,并基于进化算法对问题进行求解.
在应急设施位置已知的情况下,设施服务区划分可转化为多旅行商问题求解.多旅行商问题(Multiple Traveling Salesman Problem,MTSP)是在传统的旅行商问题(Travelling Salesman Problem,TSP)基础上引入多个旅行商和对应多个出发城市的变种问题.事实上,存在多个应急设施的服务区划分问题,与多起点的MTSP(旅行商位于不同的出发城市)存在共通之处.通常可将应急设施视为虚拟的旅行商,应急设施服务容量为旅行商携带的商品数量,M为应急设施个数,则虚拟旅行商的旅行路径即可匹配为应急设施的服务区域.通过应急设施服务区划分,可以将多仓库多约束的应急调度问题转换为多个单仓库的应急调度问题,并预处理相关约束条件,再利用传统的VRP 或TSP 方法进行应急路径规划.针对此类问题,Steven等[4]采用聚集聚类方法对多起点的MTSP进行求解.Liu等[5]利用图论将MTSP分解为TSP,再进行模型最优解的获取.此外,Alencar等[6]具体研究MTSP在物资配送、路径规划方面的实际应用,并提出了相应算法对问题求解,基本思路为先通过旅行商旅行路径划分服务区域,再进行路径规划.
基于MTSP 的应急设施服务区划分研究较为不足,可以看出:MTSP 契合多设施多集散中心的应急设施服务区划分问题特征,具有重要的研究应用价值.本文构建一种基于MTSP的应急设施服务区划分模型,并利用针对P-中值选址模型的整数规划方法及禁忌搜索算法,结合LKH 求解器提出一种复合算法对模型进行求解,从而为物资配送及各类紧急救援方案的制定提供依据.
1 模型构建
基于MTSP 构建一种应急设施服务区划分模型,将各应急设施视为虚拟旅行商,在网络需求,资源供应,流量平衡等约束条件下,以最小化遍历区域内全部集散中心的综合旅行时间成本为优化目标,获取模型最优的区域应急设施服务区划分方案.
1.1 基本假设
(1)具备先进的应急调度系统及信息更新方式,所有应急设施信息共享,均服从系统的联合管理,以综合效益最大化进行服务区划分.各应急设施的位置及资源储存情况已知,且能够满足区域内的全部资源需求.
(2)各个集散中心的位置及资源需求已知,且基于公平原则进行资源获取.
(3)应急车辆的每次运输均从其所属的应急设施出发,前往服务区内的集散中心发放物资,并最终返回该应急设施.
1.2 参数及变量
(1)参 数.
N——节点集合,N=E∪D;
Z——应急设施服务区域集合;
D——应急设施集合;
E——集散中心集合;
nz——应急设施服务区数量;
nd——应急设施数量;
ne——集散中心数量;
——集散中心i的资源需求数量,i∈E;
rj——应急设施j的资源供应数量,j∈D;
dxy——邻接矩阵中节点x到节点y的应急车辆行程时间,x,y∈N;
(2)变 量.
决策变量:
——若,表示集散中心i被分配至应急设施j;若,表示集散中心i未被分配至应急设施j.
中间变量:
μxy——旅行商从节点x出发前往节点y的次数,若μxy=0,表示旅行商未从节点x出发前往节点y;
Ej——应急设施j所服务的集散中心集合;
Pj——应急设施j所在的设施服务区的全部节点集合,Pj=Ej∪{j} .
1.3 模型结构
(1)目标函数.

(2)约束条件.

式(1)为模型优化目标函数,要求最小化遍历区域内全部集散中心的综合旅行时间成本.式(2)确保每个服务区均围绕一个应急设施进行划分.式(3)确保在同一个应急设施服务区内,任意集散中心必然与该服务区内的应急设施或其他集散中心邻接,换而言之,保证设施服务区的聚团划分.式(4)确保任意一个应急设施服务区内的集散中心物资需求总量不能超过该服务区应急设施的资源供应数量.式(5)确保各个应急设施被分配的集散中心数量之和等于集散中心总数.式(6)要求每个集散中心仅被分配至一个应急设施.因此,式(5)和式(6)共同构成集散中心全覆盖约束.式(7)确保网络中的应急设施资源总量可以满足全部资源集散需求.式(8)为流量平衡约束,保证任意节点的旅行商抵达次数等于该节点的旅行商出发次数.
2 求解算法
MTSP 是TSP 的变种形式,属于组合优化问题,在计算复杂度上属于NP 困难问题,难以精确求解.因此,本文基于P-中值选址模型的优化理念及禁忌搜索(Tabu Search,TS)算法,结合LKH求解器(Lin-Kernighan-Helsgaun TSP solver)对所构建的应急设施服务区划分模型求解.
禁忌搜索算法是一种全局逐步寻优的亚启发式算法,可有效求解NP困难问题[7].LKH求解器是当前求解TSP 及其变种问题的有效工具,其求解速度快,解的优越性高,可以为目前所有能够精确求解的TSP实例找到最优解.
首先参考P-中值选址模型的优化理念,利用整数规划方法形成初步可行的设施服务区划分方案;然后基于禁忌搜索算法的理念,通过迭代方式,不断选取集散中心执行移动、交换操作;调用LKH 求解器计算目标函数值的变化,使初始方案向目标函数优化方向搜索,最终获得模型的局部最优解.算法流程如图1所示,详细步骤如下.
Step 0初始化.输入应急设施集合D,设施资源供应数量rj,集散中心集合E,各个集散中心的资源需求,网络中全部邻接节点之间的行程时间dxy.
Step 1参考P-中值选址模型,在约束条件下,以最小化总资源旅行成本,即集散中心到应急设施的旅行时间成本与集散中心资源需求数量的乘积和为优化目标,初步划分应急设施服务区.具体而言,可以通过Dijkstra算法获取各个集散中心到各个应急设施的最短路径,然后将集散中心资源需求数量作为权重系数,以归属关系作为0-1变量直接求解,形成服务区划分初始可行解.
Step 2将应急设施j作为虚拟旅行商,以总旅行时间成本最小为目标对其服务区域内的集散中心进行遍历,即将问题转化为TSP问题.在此基础上,通过LKH 求解器快速求解其最小的TSP 时间成本.以此类推,获得各应急设施服务区的最小TSP时间成本,得到初始可行解的目标函数值Ttsp.
Step 3将当前模型最优解作为禁忌对象,执行禁忌搜索.设置备选搜索步长为{0,1,2,3},禁忌长度为4,最大迭代次数为nmax,T0=Ttsp,n=0,l=0.
Step 4从当前模型最优解中随机选择应急设施服务区域z1,从剩余区域集合中随机选择一个与z1邻接的区域z2.执行z1→z2,根据邻接矩阵筛选出区域z1中与区域z2直接相连的集散中心,并将这些集散中心纳入集合r1.随机选择搜索步长Mmove1,r1中随机选择Mmove1个集散中心,并将这些集散中心从区域z1中移到区域z2中.
Step 5更新区域z1,z2.执行z2→z1,根据邻接矩阵筛选出区域z2中与区域z1直接相连的集散中心,并将这些集散中心纳入集合r2.随机选择搜索步长Mmove2,r2中随机选择Mmove2个集散中心,并将这些集散中心从区域z2中移到区域z1中.
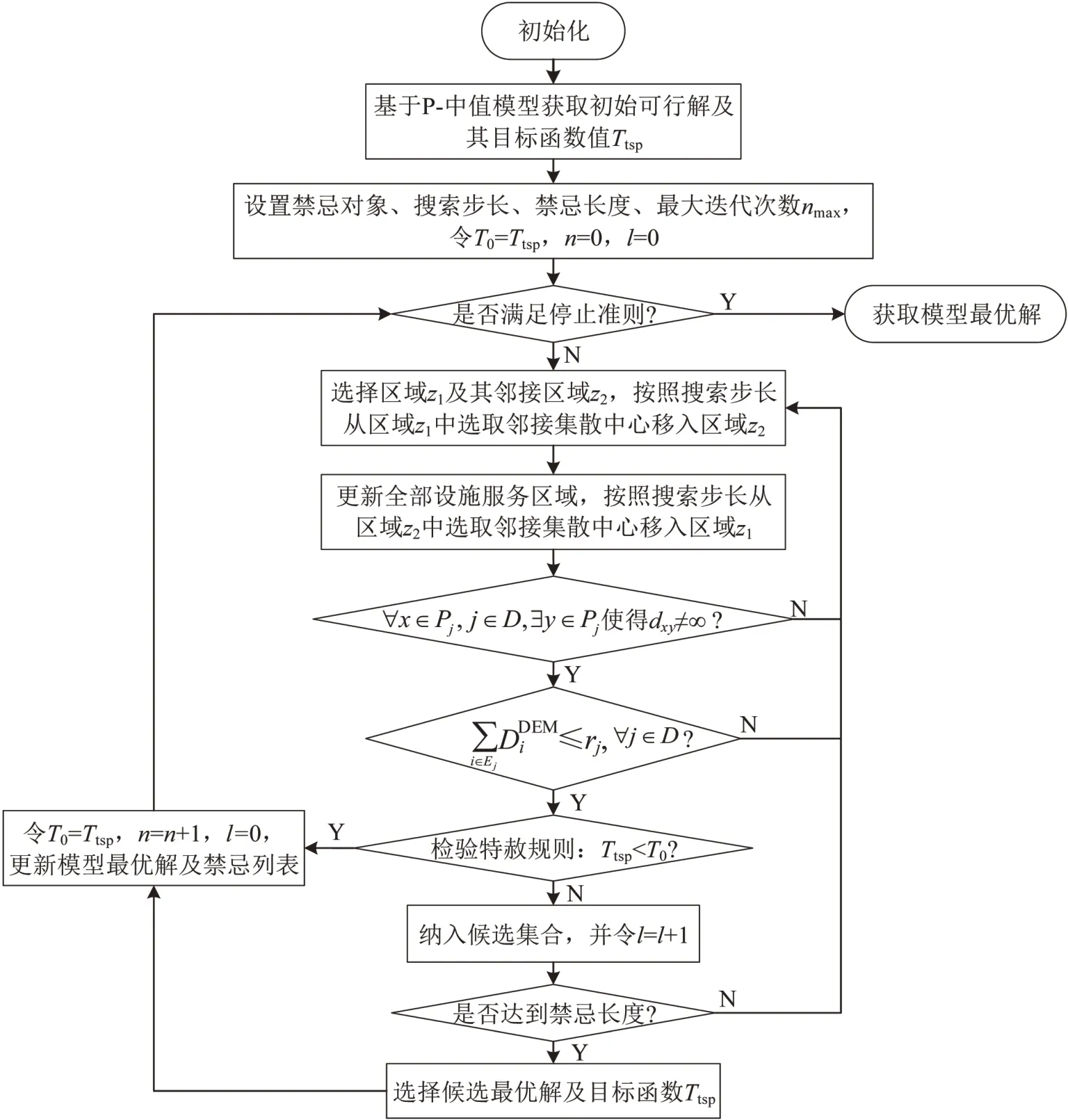
图1 算法流程Fig.1 Algorithm flowchart
Step 6基于式(3),检验集散中心的连续性,确保服务区域聚团分布. 如 果∀x∈Pj,j∈D,∃y∈Pj使得dxy≠∞,则进入Step 7;反之,重新进入Step 4.
Step 7基于式(4),检验应急设施资源容量约束.如果,则进入Step 8;反之,重新进入Step 4.
Step 8计算当前候选解的目标函数值Ttsp,检验是否满足特赦规则.若Ttsp<T0,则直接将该候选解替换为模型最优解,更新禁忌列表,令T0=Ttsp,n=n+1,l=1,并重新进入Step 4;反之,令l=l+1,进入Step 9.
Step 9检验是否已达到禁忌长度. 如果l≥4,则进入Step 10;反之,重新进入Step 4.
Step 10以模型目标函数作为评价标准,选择候选集合中的最优解及其目标函数值Ttsp,替换该候选最优解为模型最优解,更新禁忌列表,令T0=Ttsp,n=n+1,l=0,并重新进入Step 4.
终止条件:迭代次数n≥nmax.此时,对应于当前T0的应急设施服务区划分方案即为模型最优解.
3 案例分析
基于浙江省宁波市北仑区实际拓扑网络进行案例分析.网络布局如图2 所示,该区域内共有39条路段,23个交叉口,以及分别位于节点24,25,26的3 处应急设施,具体道路参数如表1 所示.现假设该区域内发生突发公共卫生事件,并产生应急资源调度需求.为确保资源集散的可达性,集散中心设置于各路段中点,网络中各集散中心的资源需求数量及应急设施的资源供应数量如表2和表3所示(以防护服为例).
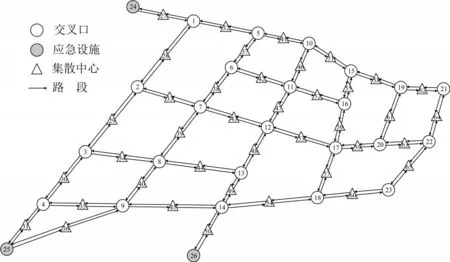
图2 北仑区道路网络Fig.2 Road network of Beilun District

表1 网络道路属性表Table 1 Road property in network
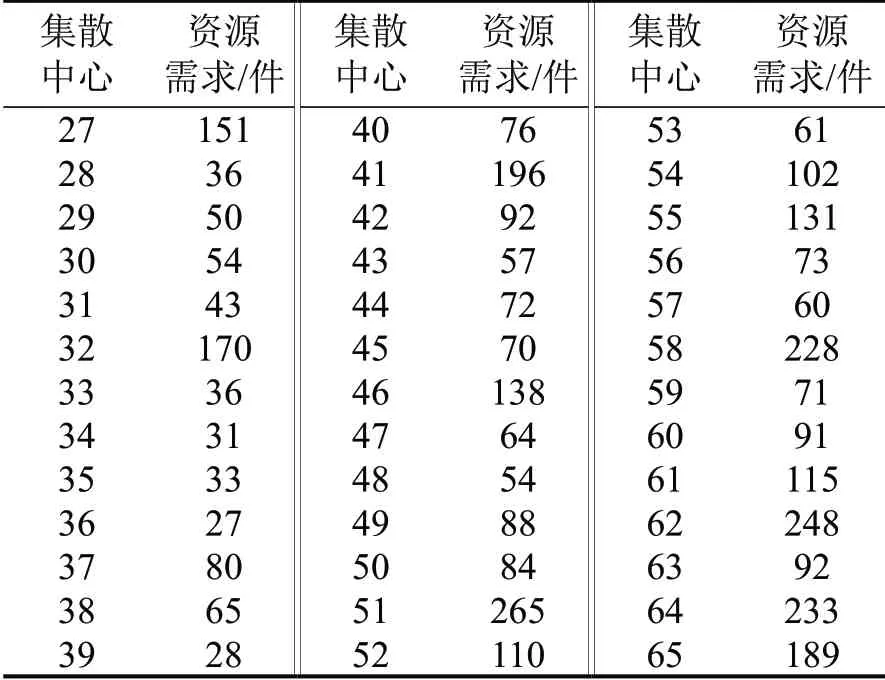
表2 集散中心资源需求数量Table 2 Resource demand of distribution centers

表3 应急设施资源供应数量Table 3 Resource supply of emergency facilities
假设网络上设有应急专用车道,应急车辆路段通行速度为60 km/h,获得模型最优解如图3 所示.该方案满足模型的全部约束条件,划分出的3个服务区域Ⅰ、Ⅱ、Ⅲ的TSP旅行时间成本分别为632,895,825 s,服务区资源需求分别为1 229,964,1 671 件,方案遍历区域内全部集散中心的综合旅行时间成本Ttsp=2 352 s.

图3 模型最优服务区划分方案Fig.3 Model optimal service area division scheme
为证明所提模型与算法的优越性,基于参考文献[4],以应急设施到所服务集散中心的总旅行时间成本最小为优化目标,在相同的模型约束条件下,采用聚类蚁群算法进行服务区划分对照,获得对照方案如图4所示.由图4可知,划分出的3个服务区域Ⅰ、Ⅱ、Ⅲ的TSP 旅行时间成本分别为591,1 088,873 s,服务区资源需求分别为1 267,936,1 661 件,遍历区域内全部集散中心的综合旅行时间成本Ttsp=2 552 s.
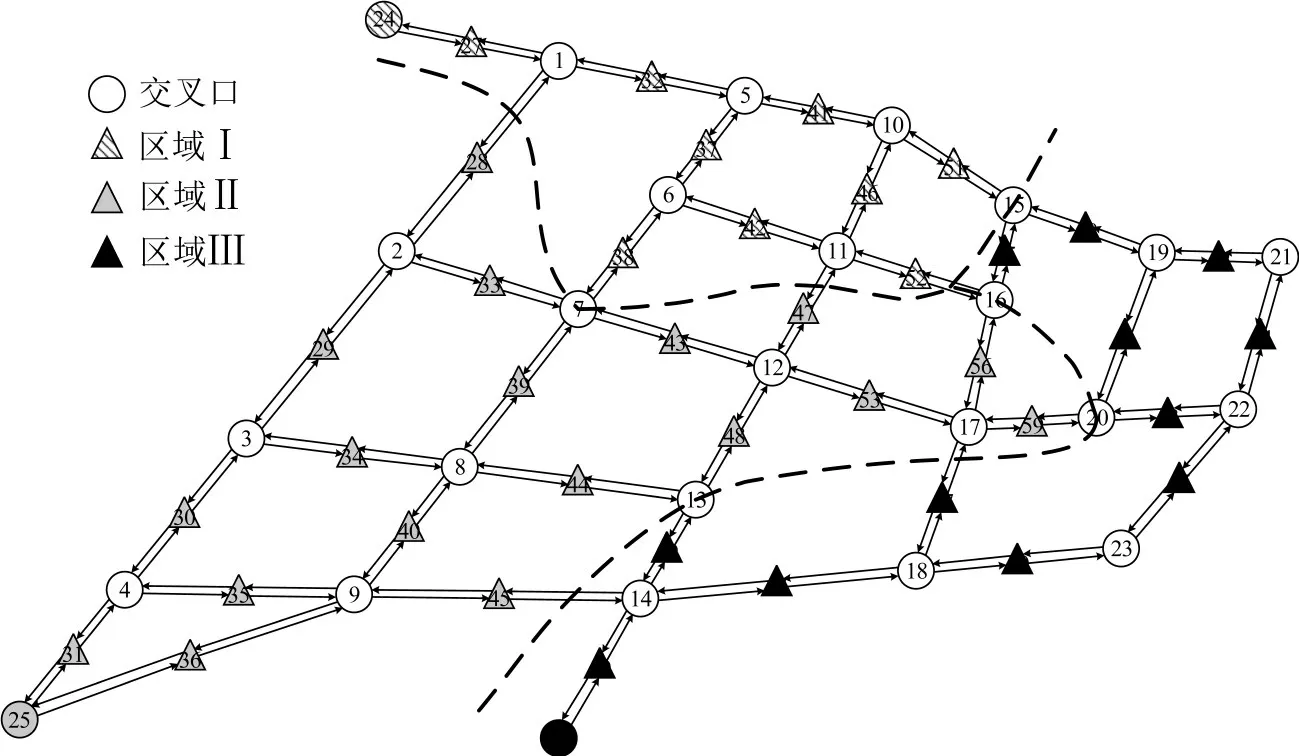
图4 服务区划分参照方案Fig.4 Service area division control scheme
对比本文模型最优方案与参照方案可以发现:在模型最优方案中,尽管部分集散中心被分配到较远的应急设施(如集散中心52距离应急设施25、26的时间成本分别为368 s、270 s,在优化过程中被从应急设施26分配至应急设施25),但是模型最优解的目标函数得到一定程度的优化,Ttsp降低了7.84%.这意味着,在各个应急设施服务区内,车辆从应急设施出发遍历该区域内全部集散中心的综合时间成本得到降低,有利于减少运输时间成本,从整体上提高物资配送或紧急救援方案的效率.
在此基础上,本文进一步假设应急设施24、25、26 处各有1 辆应急运输车辆,其车辆满载为400件防护服,基于简单插入算法[8],获得综合物资配送方案如表4 所示,其中,车辆每次从应急设施出发时更新为满载,不足满载时则更新为应急设施剩余物资容量,配送完毕后返回应急设施.
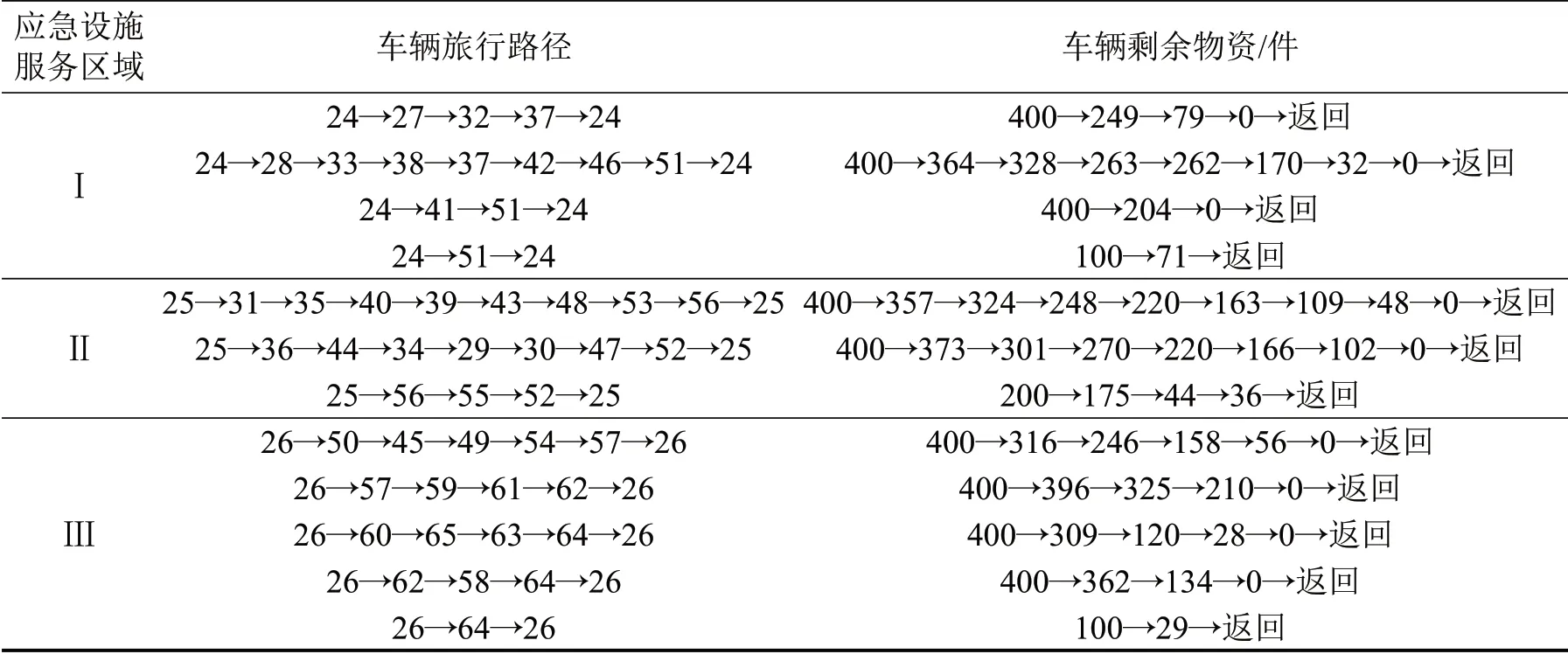
表4 综合物资配送方案Table 4 Resource distribution scheme
4 结 论
本文构建了一种基于多旅行商问题的应急设施服务区划分模型,将各应急设施视为虚拟旅行商,以最小化遍历区域内全部集散中心的综合旅行时间成本为优化目标划分应急设施服务区域,并设计一种复合算法对模型进行求解.经过实例验证,该模型可以有效解决应急设施服务区划分问题,提高物资配送或紧急救援方案的效率.下一步将在本文研究基础上,探究如何采用更合理的方法进行各应急设施物资配送或紧急救援的路径规划,以及应急设施位置未知情况下的应急设施选址—路径问题.

