一类具有时滞的麻疹传染病模型的全局分析
王 茉,刘俊利
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
传染病对人类危害巨大,并且破坏范围极广。在过去的数十年里,全世界范围内爆发过多种传染疾病,例如非典、肺结核、流感、麻疹、埃博拉等。这些传染病使人闻之色变,每一次的出现都会给家庭以及社会带来巨大的损失。因此,传染病的控制一直以来都是学者们研究的重要课题[1-5]。其中,麻疹是由麻疹病毒感染引起的急性呼吸道传染病,极易在人群中传播并导致各种并发症。麻疹易感人群包括因太小(8月龄之前)还没有接种过疫苗的幼儿,以及没有接种过疫苗的成人,麻疹一年四季均可感染,但3~5月是发病高峰期[6-8]。自从麻疹疫苗发明以来,全世界麻疹的死亡率一直在下降,但发展中国家以及一些贫困地区疫苗接种尚未得到广泛普及,麻疹仍是造成全球幼儿死亡的主要原因之一。因此,建立并研究麻疹传播动力学模型对疫情控制意义重大。
目前,国内外许多学者针对麻疹疾病的接种免疫、传播规律等都做了诸多研究。PANG等建立了一类具有接种的麻疹模型,讨论了接种疫苗对于控制麻疹传播的作用,并分析得到了麻疹疫苗接种覆盖率的2个临界阈值[9];姜翠翠等建立了具有部分免疫和潜伏期的麻疹模型,计算得到模型的基本再生数,讨论了模型的稳定性并分析了潜伏期以及免疫活动对于基本再生数的影响[10];HUANG等考虑了一类带有周期性传染率的麻疹模型,研究了季节性麻疹流行和疫苗接种对麻疹传播的影响,并利用数值模拟验证了理论结果的正确性[11]。但随着对麻疹发病机制的深入研究,发现麻疹在染病初期并未出现斑疹症状,而是在潜伏期之后才开始逐渐出疹,通常利用“时滞”来描述这一传播机理,即患者的发病状态变化不仅取决于当前时刻的影响,还受前一时刻因素的影响。本文在文献[11]的基础上考虑了时滞因素对于麻疹疾病传播的影响,建立并分析了一类带有时滞的微分方程麻疹模型,并证明了各平衡点的全局渐近稳定性。
1 模型建立
将总人口N(t)分为S(t)、E(t)、I(t)、R(t)等4类,分别表示t时刻人群中的易感者人数、潜伏者人数、染病者人数和恢复者人数,模型如下:
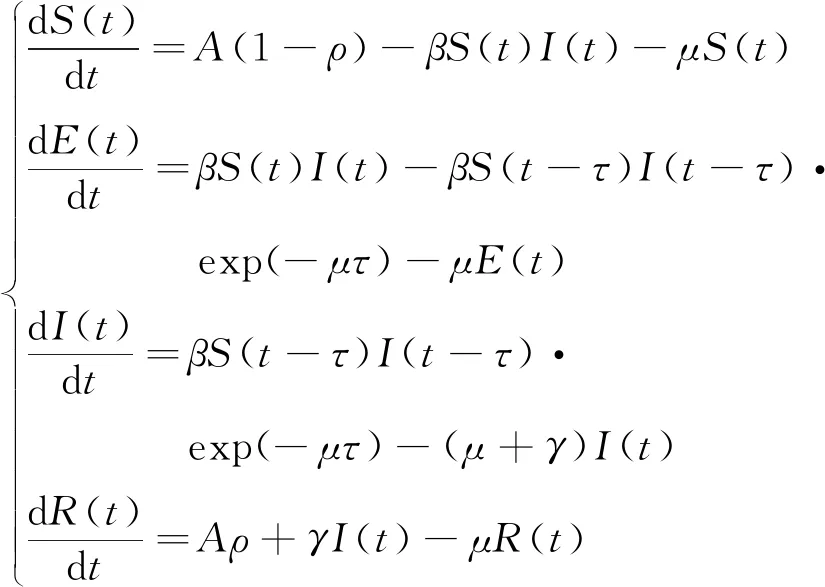
(1)
式中:A为人口的输入率;ρ为接种率(0<ρ<1);μ为人口自然死亡率;β为麻疹的感染率;γ为疾病恢复率;τ为麻疹的潜伏期。

定义集合
定理1 ∀φ∈χ,模型(1)有唯一的非负解u(t,φ),u0=φ,t∈[0,∞),且半流Φ(t)=ut(·):χ→χ具有紧的全局吸引子。
证明给定φ∈χ,定义G(φ):=(G1(φ),G2(φ),G3(φ),G4(φ)),其中
G1(φ)=A(1-ρ)-μφ1(0)-βφ1(0)φ3(0)
G2(φ)=βφ1(0)φ3(0)-βφ1(-τ)φ3(-τ)·
exp(-μτ)-μφ2(0)
G3(φ)=βφ1(-τ)φ3(-τ)exp(-μτ)-
(μ+γ)φ3(0)
G4(φ)=Aρ+γφ3(0)-μφ4(0)
因为χ在C中是闭的,∀φ∈χ,G(φ)在R×χ中每个紧集上都是连续的,关于φ是Lipschitz连续的。根据文献[12]中定理2.3可知,∀φ∈χ,模型(1)通过点(0,φ)的解在其最大存在区间[0,σφ)上是唯一的。
由模型(1)的第二式,可以得到
exp(μt)(E′(t)+μE(t))=exp(μt)(βS(t)I(t)-
βS(t-τ)I(t-τ)exp(-μτ))
两边积分得


即∀t∈[0,σφ),ut∈χ。


2 基本再生数和平衡点的局部稳定性
显然模型(1)总存在唯一的无病平衡点Q0=(S0,0,0,R0),其中
根据文献[15-16],计算得到模型(1)的基本再生数为
(2)
下证R0>1时,模型(1)还存在地方病平衡点Q*=(S*,E*,I*,R*),Q*应该满足方程:
化简有
因此,当且仅当R0>1时,模型(1)有唯一的地方病平衡点Q*。
下面证明平衡点Q0=(S0,0,0,R0)和Q*=(S*,E*,I*,R*)的局部稳定性。
定理2 如果R0<1,则模型(1)的无病平衡点Q0是局部渐近稳定的;如果R0>1,则Q0不稳定。
证明在无病平衡点Q0处对模型(1)进行线性化,得到其特征方程为

该特征方程存在3个相等的负的特征根,即λ1=λ2=λ3=-μ,其余的特征根满足
λ+μ+γ-βS0exp(-μτ)exp(-λτ)=0
(3)
当τ=0时,式(3)变为
λ+μ+γ-βS0=0
则
λ=βS0-μ-γ=(μ+γ)(R0-1)
因此,当R0<1时,λ<0,特征方程的所有根都是负数,则Q0是局部渐近稳定的;反之,当R0>1时,λ>0,特征方程有一个正根,则Q0是不稳定的。
当τ>0时,令λ=iω,ω∈R。将λ代入式(3)得
iω+μ+γ-βS0exp(-μτ)exp(-iωτ)=0
(4)
分离式(4)的实部和虚部,得
则有
(μ+γ)2+ω2=(βS0exp(-μτ))2
即
ω2=(βS0exp(-μτ)+μ+γ)·
(βS0exp(-μτ)-μ-γ)=
(μ+γ)(βS0exp(-μτ)+
μ+γ)(R0-1)
因此,当R0<1时,上式无解。综上所述,∀τ≥0,当R0<1时,式(2)的所有根均具有负实部,此时无病平衡点Q0是局部渐近稳定的,当R0>1时,Q0是不稳定的。
下面讨论地方病平衡点Q*的局部稳定性。
定理3 当R0>1时,地方病平衡点Q*=(S*,E*,I*,R*)是局部渐近稳定的。
证明在地方病平衡点Q*处,对模型(1)进行线性化,得到其特征方程为

化简上述方程,得到
则该特征方程存在2个相等的负的特征根,即λ1=λ2=-μ,其余的特征根满足下式:
λ2+(x1+x2)λ+(x3-x1x2-x2λ)·
exp(-λτ)+x1x2=0
(5)
其中
x1=μ+βI*,x2=μ+γ,
x3=β2S*I*exp(-μτ)
当τ=0时,式(5)为
λ2+x1λ+x3=0
显然此时式(5)的所有根均具有负实部。
当τ>0,令λ=iω,ω∈R,将λ代入式(5),得:
(iω)2+(x1+x2)iω+(x3-x1x2-x2iω)·
exp(-iωτ)+x1x2=0
化简并分离实虚部得:
(6)
式(6)左右两边分别平方并求和得:
(7)

3 平衡点的全局稳定性
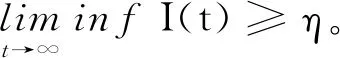
证明定义
X0={φ=(φ1,φ2,φ3,φ4)∈χ:φ3(0)≠0}
则有
∂X0=χX0={φ∈χ:φ3(0)=0}
定义
M∂={φ∈χ:Φ(t)φ∈∂X0,∀t≥0}
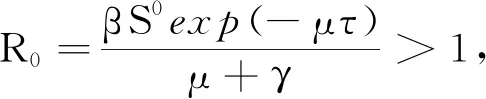
推断1 ∀φ∈X0,有

(8)
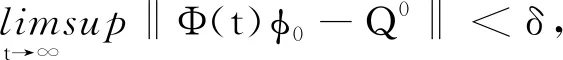
I(t-τ)-(μ+γ)I(t)
推断2 ∪φ∈M∂ω(φ)=Q0。
∀φ∈M∂,Φ(t)φ∈∂X0,即I(t,φ)≡0,由模型(1)的第二、第三和第四式有
则
∪φ∈M∂ω(φ)=Q0
定义连续函数p:χ→R+:
p(φ)=φ3(0),∀φ∈χ
显然,p-1(0,∞)⊂X0,p具有以下属性:∀t>0,p(φ)=0,或者φ∈X0时,p(φ)>0,则p(Φ(t)φ)>0。因此,p是半流Φ(t):χ→χ的广义距离函数。由推断2知Φ(t)在M∂中的任何正向轨道都收敛于Q0。由推断1知,Q0是χ中的一个孤立不变集,并且Ws(Q0)∩X0=ø。此外,在∂X0中{Q0}没有形成一个循环,由文献[18]中定理3可知,∃η>0,∀φ∈X0,使得

则一致持久性证明成立。
定理5 如果R0<1,则无病平衡点Q0=(S0,0,0,R0)是全局渐近稳定的。

(9)
因为
考虑辅助方程
则有
由比较原理知
则∃T>0,使得∀t>T,有
由模型(1)中第三式得,当t>T+τ时,有
I(t-τ)-(μ+γ)I(t)
考虑辅助方程
(μ+γ)y(t)
由式(9)和文献[17]中引理2.1知

由比较原理知
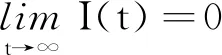
则模型(1)的极限方程为
易知,当t→∞时,有
结合定理2知,当R0<1时,无病平衡点Q0=(S0,0,0,R0)是全局渐近稳定的。
定理6 如果R0>1,则地方病平衡点Q*=(S*,E*,I*,R*)是全局渐近稳定的。
证明在模型(1)中首先考虑第一和第三式:
定义S(t)=S(t),U(t)=I(t+τ),则上式等价于

(10)
V(t)=V1(t)+V2(t)+V3(t)
式中:
沿系统(10)的解曲线计算函数V(t)的导数,则有
则有

因此
因此模型(1)的每个解都趋于平衡点Q*=(S*,E*,I*,R*),从而再由定理3可知,地方病平衡点Q*是全局渐近稳定的。
从分析模型基本再生数可以得出:R0是感染率β的增函数,降低感染率可以减小基本再生数,即减少被感染麻疹的人数;R0是接种率ρ和治愈率γ的减函数,通过增大对新生儿的接种率ρ以及增加麻疹染病患者的治愈率γ也可以减小基本再生数,即减少了麻疹易感者的人数。
4 结 语
本文在文献[10]的基础上,研究了一类具有时滞因素影响的麻疹数学传播模型,分析了模型平衡点的存在性和唯一性,并计算得到模型的基本再生数R0。此基本再生数R0完全决定了模型的动力学行为:对任意的时滞τ≥0,当R0<1时,模型(1)的无病平衡点Q0是全局渐近稳定的,即疾病绝灭;当R0>1时,无病平衡点不稳定,模型(1)还存在唯一的地方病平衡点,且地方病平衡点全局渐近稳定。说明该地区麻疹染病现象将长期存在,并逐渐发展成为地方病。降低感染率β,增大新生儿接种率ρ,提高麻疹染病患者的治愈率γ均有利于减少麻疹患者的人数。

