一类基于时间-迭代信号的切换系统ILC策略

杨 轩，耿 燕

(西安工程大学 理学院，陕西 西安 710048)

0 引 言

切换系统是一个由一系列连续或离散子系统以及协调这些子系统之间进行切换的规则组成的混合系统[1-2]。近年来，随着工业技术的发展，切换系统广泛地出现在各种工程实际中，从而越来越受到人们的关注。因此，对切换系统深入研究具有重要的理论意义和实用价值[3-4]，特别是对切换系统轨迹跟踪控制研究是一个突出且具有广泛发展前景的问题[5-6]。但是，由于切换系统的动态行为较为复杂，对这类系统进行跟踪控制研究也面临诸多挑战，相关理论有待进一步探究[6-8]。

在跟踪控制领域，迭代学习控制(ILC)是一种有效控制策略，近几十年来一直受到广泛关注[9-10]。 ILC策略以人脑学习机理为基础，针对在固定时间区间内重复运行的系统，通过不断地学习、改进，逐步实现对目标的精确跟踪[9]。与传统的控制策略相比，ILC突出的优点是，利用较少的系统信息就可以达到对目标准确跟踪的目的[11-12]。因此, ILC适用于具有重复性质的跟踪控制任务。尤其是当系统动力学信息未知或部分已知，初始状态可重置时，这种技术更具优越性。

切换系统的迭代学习控制在电力、交通、调度等领域具有广泛的应用。目前，关于切换系统的ILC研究已取得一定的进展：P-型[10]、PD-型[13]、D-型[14]、高阶PID-型[15]等是这类问题的早期成果。近年来，随着研究的深入，混合型ILC[16-18]和带衰减因子的ILC策略[19]等相继涌现。需要强调的是，这些控制策略都是针对由时变切换信号支配的切换系统取得的成果。而在工程实际中，还存在其他诸如时间-迭代变化的切换信号、状态驱动的切换信号以及事件驱动的切换信号等[1,20]。针对由这类切换信号支配的切换系统，上述的控制策略很难奏效。因此，有必要拓展切换系统的ILC研究。

本文针对在时间-迭代域内随机变化的切换规则，设计了一种切换系统的新型迭代学习控制算法，并通过理论分析和数值仿真验证了控制策略的可行性和有效性。

1 基本问题描述

考虑如下的线性连续切换系统

(1)

式中：k是迭代次数；Ω=[0,T]表示固定的时间区间；xk(t)∈Rn,uk(t)∈Rm，yk(t)∈Rl和ξk(t)∈Rl分别表示状态、输入、输出以及外部噪声向量;x0∈Rn是初始状态；Aτ(φ(t),k)、Bτ(φ(t),k)和Cτ(φ(t),k)是具有适当维数的系统矩阵。下标τ(φ(t),k)表示切换信号，是关于时间和迭代次数的随机常函数，定义如下：

τ(φ(t),k)=l[i,k] (i=1,2,…,n)

(2)

其中，i定义为

附注1 由切换规则定义可以看出，控制过程是将时间区间Ω随机分成n段，且Ω=Ω1∪Ω2∪…∪Ωn,Ω1∩Ω2∩…∩Ωn=∅。l[i,k]表示第k次学习周期内第i个时间区间上的一个随机数。这就意味着，不同迭代过程中的同一个时间子区间上运行的子系统随机分配(与时变切换信号支配的切换系统不同)，同一迭代周期内的不同时间子区间内运行的子系统也相互独立。在这种切换信号的支配下，在任一学习周期内的任何时间子区间内，任意子系统都有可能被调动运行。具体运行的子系统，由随机数l[i,k]指定，例如，如果l[2,5]=3，则在第5次学习过程中第2个时间子区间上，由第3个子系统运行。

在式(2)的支配下，系统(1) 可重新描述为

(3)

任意给定可达的目标轨线yd(t)(t∈Ω)，定义跟踪误差

ek(t)=yd(t)-yk(t)

考虑如下的D-型ILC算法

(4)

式中：Γl[i,k]表示微分学习增益；Φl[i,k](t)是适当维数的可逆矩阵。

通过控制算法(4)可以产生一个递归的控制序列{uk(t)}，使得在其控制下，系统(3)的输出信号随着迭代次数k的增加，渐近跟踪至yd(t)(t∈Ω)的某个邻域，即

(5)

给定向量函数v(t)：[0,T0]→Rn, 其λ-范数定义[21]为

其中‖·‖表示某种向量范数。

假设1 对于t∈Ω,任意给定目标轨线yd(t)，存在期望控制信号ud(t)和适当的期望状态xd(t)，满足

假设2 每次迭代的初始状态满足‖xd(0)-xk(0)‖<μ,k=1,2,…, 其中μ是一个充分小的正数.

假设3 外界噪声向量ξl[i,k](t)是有界的，即‖ξl[i,k](t)‖<δ, 其中δ是一个充分小的正数。

2 主要结果

引理1[22](Bellman-Gronwall不等式) 设函数h(·):[t0,T0]→R+,a,b,c≥0是常数。如果

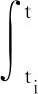
λ>a+b

则

引理2[23]考虑非负实序列{ak}，满足

ak≤σ1ak-1+σ2ak-2+…+σNak-N+εk,

k=N+1,N+2,…

式中：al(l=1,2,…,N)为初始值； {εk}为界定数列。如果系数σj(j=1,2,…,N)满足σj≥0，且

定理1 将迭代学习控制算法(4)应用于由切换信号系统(2)支配的切换系统(3)，如果存在适当的学习增益Γl[i,k]和非奇异矩阵Φl[i,k](t)满足

(6)

则随着迭代次数k的增加，系统(3)的输出信号yk(t)(t∈Ω)渐近跟踪yd(t)(t∈Ω)到其某个邻域内。

证明系统(3)在第k-次学习周期内的状态

响应为

则系统的输出信号为

由跟踪误差的定义，得

(7)

存在非奇异矩阵Θl[i,k](t)和Φl[i,k](t), 使得

(8)

因此，跟踪误差的递归关系式(7)变为

(9)

式中：δxk(ti-1)=Θl[i,k](t)xk+1(ti-1)-xk(ti-1);Δξl[i,k](t)=ξl[i,k+1](t)-ξl[i,k](t)。

应用学习算法(4)，式(9)可变为

ek+1(t)=ek+1(t)-Cl[i,k]·

exp(Al[i,k](t-ti-1))δxk(ti-1)-

利用分部积分法，得

(10)

对式(10)分步骤分析如下:

1) 当t∈Ω1时,某个子系统在Ω1运行,而且不同学习周期运行在此区间上的子系统可能不同，由切换律指定。记t0=0，则跟踪误差的递归关系(10)可变为

(11)

对式(11)两边取范数并利用范数不等式，得

(12)

式中：

al[1,k]=‖Al[1,k]‖

bl[1,k]=‖Bl[1,k]‖,cl[1,k]=‖Cl[1,k]‖

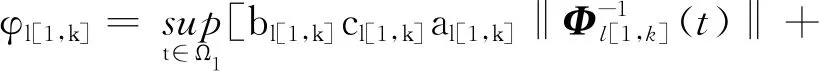
‖Θl[1,k](t)xk+1(0)-xk(0)‖]

将等式(12)两边同时乘exp(-λt) (λ>al[1,k])，得

由于子系统的个数以及子系统矩阵维数都是有限的，考虑假设2可得，φl[1,k]、φl[1,k]和κl[1,k]都是有限值。

记a1=maxal[1,k],c1=maxcl[1,k]和φ1=

maxφl[1,k],并结合λ-范数，可得

式中：

εl[1,k]=φl[1,k]+κl[1,k]

由引理1得，当λ>φ1+a1时，

成立。显然, 此时不等式

成立。于是，可得

考虑条件(6)并利用引理2，得

因此，可以断定系统的输出信号在Ω1上可跟踪到目标轨线的某个邻域内。

2) 当t∈Ω2时，另一个子系统在Ω2上运行，跟踪误差的递归关系(10)可变为

Γl[2,k]]ek(t)+

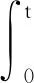
Cl[2,k]exp(Al[2,k]t)·

[Θl[2,k](t)xk+1(t1)-xk(t1)]+

Cl[2,k]exp(Al[2,k](t-t1))·

Γl[2,k]ek(t1)-Δξl[2,k](t)

(13)

对式(13) 两边同时取范数，得

(14)

式中：

将等式(14) 两边同时乘以exp(-λt) (λ>al[2,k]),得

因为系统输出在第一个子区间上可以跟踪目标轨线到某个邻域内，参数φl[2,k],φl[2,k]和κl[2,k]都有界。为了表示方便, 记a2=maxal[2,k],c2=

maxcl[2,k]和φ2=maxφl[2,k]。于是，可得

式中：

εl[2,k]=φl[2,k]+κl[2,k]

由引理1得，当λ>φ2+a2时，不等式

成立。显然，此时不等式

成立。于是，有

(15)

于是，系统在时间区间Ω2上可跟踪目标轨线到其某个邻域。

3) 当t∈Ωi(i=3,4,…,n)时，类似地，在此时间区间上，可得不等式

当i=3,4,…,n时均成立。即系统 (2)在时间子区间Ωi上可以跟踪目标轨线于某个邻域内。进而，在整个时间区间Ω=[0,T]上均可跟踪目标轨线于某个邻域内。证毕。

附注2 显然，如何计算矩阵Φl[i,k](t)是设计ILC控制律(4)的关键之一。由等式(8)可知，其值由系统动态学信息界定。因此，当系统信息已知时，可以很方便地计算出矩阵Φl[i,k](t)。但是，在工程实际中，被控对像信息往往是未知的或部分已知的。在此情况下，计算矩阵Φl[i,k](t)比较困难。一种可行的方法是，根据以前的学习信息，辨识系统参数信息，进而计算Φl[i,k](t)的近似值。目前，关于矩阵Φl[i,k]的计算仍然是一个具有挑战性的问题，有待在后续的工作中进一步研究。

3 数值仿真

为了验证上述理论的有效性，引入一个仿真实例。考虑包含2个子系统的线性切换系统(2)，其子系统动态学信息如下:

假设切换信号l[i,k]是一个二元随机常函数，其函数值在每次迭代每个时间子区间上都随机产生，设定为10以内的随机正数。规定:如果l[i,k]在第k次迭代时第i个子区间上的数值是奇数，则第一个系统运行；否则，第二个系统运行。

由于被控对象是单输入单输出系统，则Φl[i,k](t)蜕变为一个数量值函数，可表示为Φl[i,k](t)=φ(t)/φ(t)或Φl[i,k](t)=φ(t)/φ(t)。根据参与运行的子系统的顺序,选取2种函数中的一种， 其中:

此时，收敛条件(6)中的范数

‖I-Cl[i,k]Bl[i,k]Φl[i,k](t)Γd,l[i,k]‖

蜕变为

|I-Cl[i,k]Bl[i,k]Φl[i,k](t)Γd,l[i,k]|

在后续的数值仿真中，微分学习增益统一选作Γl[i,k]=0.8。此时，ρi共有4种可能的结果：ρ1=0.417 1，ρ2=0.496 0,ρ3=0.333 9,ρ4=0.424 0。满足定理1中ρi<1的收敛条件。

假设时间区间为Ω=[0,1], 采样步长设为Δt=0.02 s。设期望轨线为

yd(t)=-t2+t(t∈Ω)

假设初始状态满足‖x0-xd(0)‖2≤0.01, 初次迭代时选取控制信号u0(t)=0。仿真结果如图1和图2所示，其中跟踪误差在l2范数意义下度量。由图1可以看出，在学习的过程中，跟踪误差的上界小于0.4;由图2可知，通过150次学习，系统可以跟踪期望轨线yd(t)(t∈Ω)于一个较小的邻域。结果与定理1的结论保持一致。

图 1 l2范数意义下误差曲线Fig.1 Error curve in the sense of l2 norm

图 2 第150次学习跟踪效果Fig.2 Tracking performance at the 150th iteration

4 结 语

本文针对一类由任意时间-迭代变化的切换信号支配的线性连续切换系统，提出了一种新型迭代学习控制算法；借助于λ-范数，导出了一个使算法收敛的充分条件。数据仿真结果表明，当学习增益的选取满足收敛条件且切换信号在时间-迭代域随机变化时，系统在ILC策略控制下，跟踪效果良好。