G-布朗运动环境下可转换债券定价及实证分析
呼 苗,薛 红,刘 欣
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
可转换债券作为一种兼具股性与债性的金融产品,一直是金融数学的热点问题之一。 国外的可转换债券的定价研究起步较早,1973年Black-Scholes期权定价理论[1]的出现为可转债定价的发展提供了重要的理论依据。 随后,INGERSOLL以公司价值为基础变量,结合Black-Scholes模型并运用无套利原理得到了一个解析解[2]。 由于公司价值在市场中并不能准确获取,McCONNELL等提出以股价作为基础变量来建立可转债定价模型,把可转换债券的价值分为纯债券价值与期权价值,并以Black-Scholes期权定价公式求解期权部分的价值[3]。 但实证研究发现Black-Scholes模型中波动率为常数的假设并不符合实际金融市场,实际波动率并不为常数,甚至是不确定的,股价波动率呈现波动率微笑,尖峰厚尾等统计特征。
为此,学者们提出了一系列随机波动率模型。SCOTT假定波动率服从指数过程[4],HULL等假定波动率服从平方根过程[5],这些模型将波动率看作由第二个布朗运动驱动的随机过程。但是金融市场数据只支持波动率有界的假定,在此基础上,LEVY等提出了不确定波动率模型,利用随机控制技术,得到了欧式期权的对偶公式,但要求欧式期权不是路径依赖型的,并指出解决此问题最大的难点在于处理一族不受控制的概率测度族,此类问题很难在概率框架下解决[6]。PENG通过偏微分方程定义了一类非线性算子G-期望及条件G-期望,研究表明G-期望可表示为一族概率测度下期望的上确界,还给出了G-布朗运动及其相关性质[7],并得到了Ito公式[8]。随后,文献[9]提出了G-框架下的Girsanov定理,为利用G-布朗运动来描述有价证券的价格变动提供了理论依据。
目前G-布朗运动相关研究多用于期权定价,还未广泛应用于可转换债券市场,考虑到可转换债券内嵌看涨期权的特点,本文利用G-布朗运动刻画标的资产价格的变化,建立金融市场数学模型,得到了G-布朗运动环境下的可转换债券定价公式,由于G-期望难以计算,在文献[7-9]的基础上,采用G-框架下的相关理论及定义对标的资产价格进行数值模拟,结合蒙特卡洛方法对可转换债券定价。并通过实证分析与传统Black-Scholes模型定价结果作对比分析。
1 G-布朗运动环境下金融市场
数学模型
定义1[10]次线性期望空间(Ω,H,EG)上的一个随机过程{Bt,t≥0}称为G-布朗运动,如果∀n∈N及0≤t1,…,tn<+,有Bt1,…,Btn∈H,且满足:
ⅰ)B0=0;
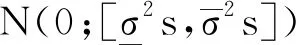
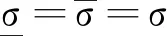
沿用文献[9]中的研究框架,利用非线性数学期望G-期望及G-框架下的Ito公式[8]建立金融市场数学模型。假设金融市场仅有2种证券。一种是无风险资产即债券,其价格满足
dMt=rMtdt
(1)
式中:r为无风险利率。另一种风险资产即股票,其价格满足
dSt=μStdt+StdBt
(2)

定理1St刻画了波动率不确定条件下的资产价格过程,则随机微分方程(2)的解
(3)
证明由G-框架下的Ito公式得
故

对∀X∈Lip(Ω),定义
则若∃ε0>0,使得
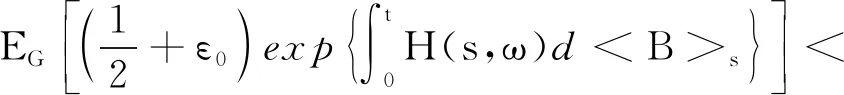
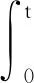
2 可转换债券定价
假定市场是无摩擦的,即市场是没有交易成本、税收,没有卖空限制,借贷利率相同,资产无限可分,资产交易在时间[0,T]上连续进行,也假定市场无套利机会。
下面用无套利思想为可转换债券定价,投资者在时刻t∈[0,T]持有无风险资产和风险资产的数量(αt,bt),那么该投资者在t∈[0,T]时刻的财富过程
Vt=αtMt+btSt,0≤t≤T
(4)
对自融资交易策略(αt,bt),其对应的财富过程{Vt,0≤t≤T}满足
dVt=αtdMt+btdSt,0≤t≤T
(5)
由式(4)~(5)有
dVt=rVtdt+bt[(μ-r)dt+dBt]
类似于文献[11],构造辅助函数dΓt=aΓtdt+bΓtdt+cΓtdBt,Γ0=1,其中a、b、c为待定常数。对ΓtVt应用Ito公式

由G-条件期望的性质[12]

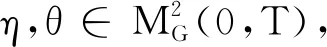

可得EG[VTΓT-VtΓt|Ft]=0,即
Vt=Γt-1EG[ΓTVT|Ft]
定理2 假定可转换债券的转换只可发生在债券到期时刻T,可转换债券在时刻T的价值VT为
(6)
式中:P表示纯债券价值;C表示转换价格;Q表示债券面值;ST表示T时刻股票价格。则G-布朗运动环境下可转换债券在0时刻价值为
(7)
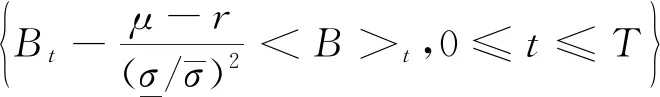
证明因为
利用引理2中G-框架下的Girsanov定理,可得0时刻可转换债券的价格为
V0=EG[ΓTVT]=
Pexp(-rT)=
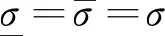
式中:P为风险中性概率测度;{Bt,t≥0}为标准布朗运动。
3 可转换债券定价数值解法
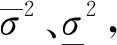
3.1 参数估计
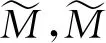
其中
3.2 股票价格轨道模拟
3.2.1G-正态分布模拟 根据上、下方差的估计值,利用标准正态分布的模拟思路[15],类似地可以模拟得到G-正态分布。
引理3[16]若X是服从G-正态分布的实值随机变量,则有
EG[φ(X)]=u(1,0),φ∈Cl,Lip(R)
(8)

(9)
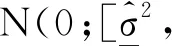
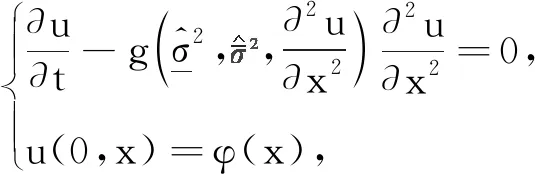
(10)
式中
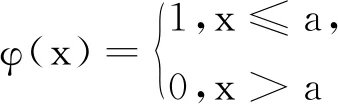
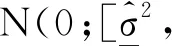
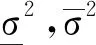
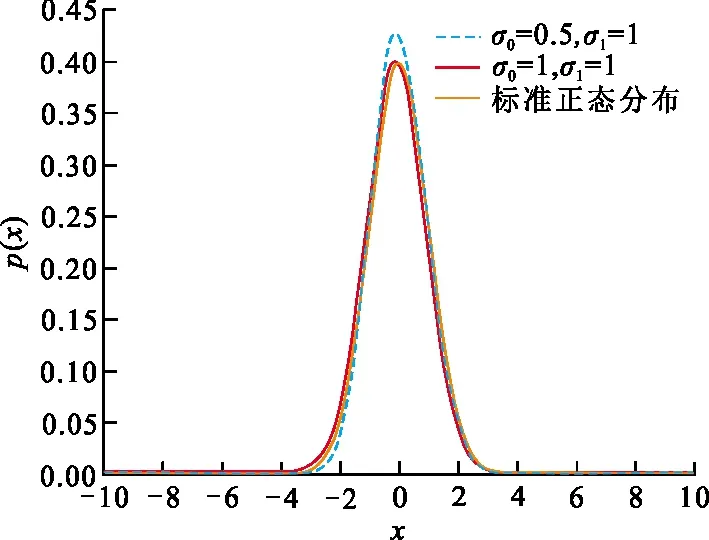
图 1 G-正态分布密度函数Fig.1 G-normal distribution density function
3.2.2G-布朗运动及二次变差过程模拟
定义2[18](二次变差过程)G-布朗运动的二次变差过程{t,t≥0}定义为
式中
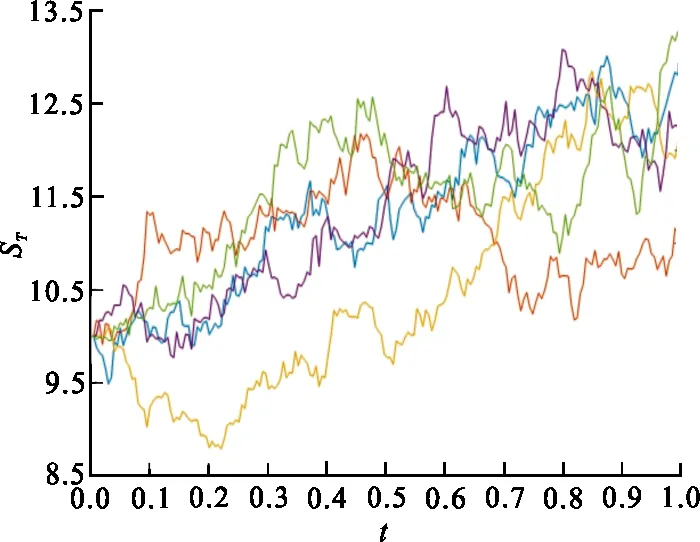
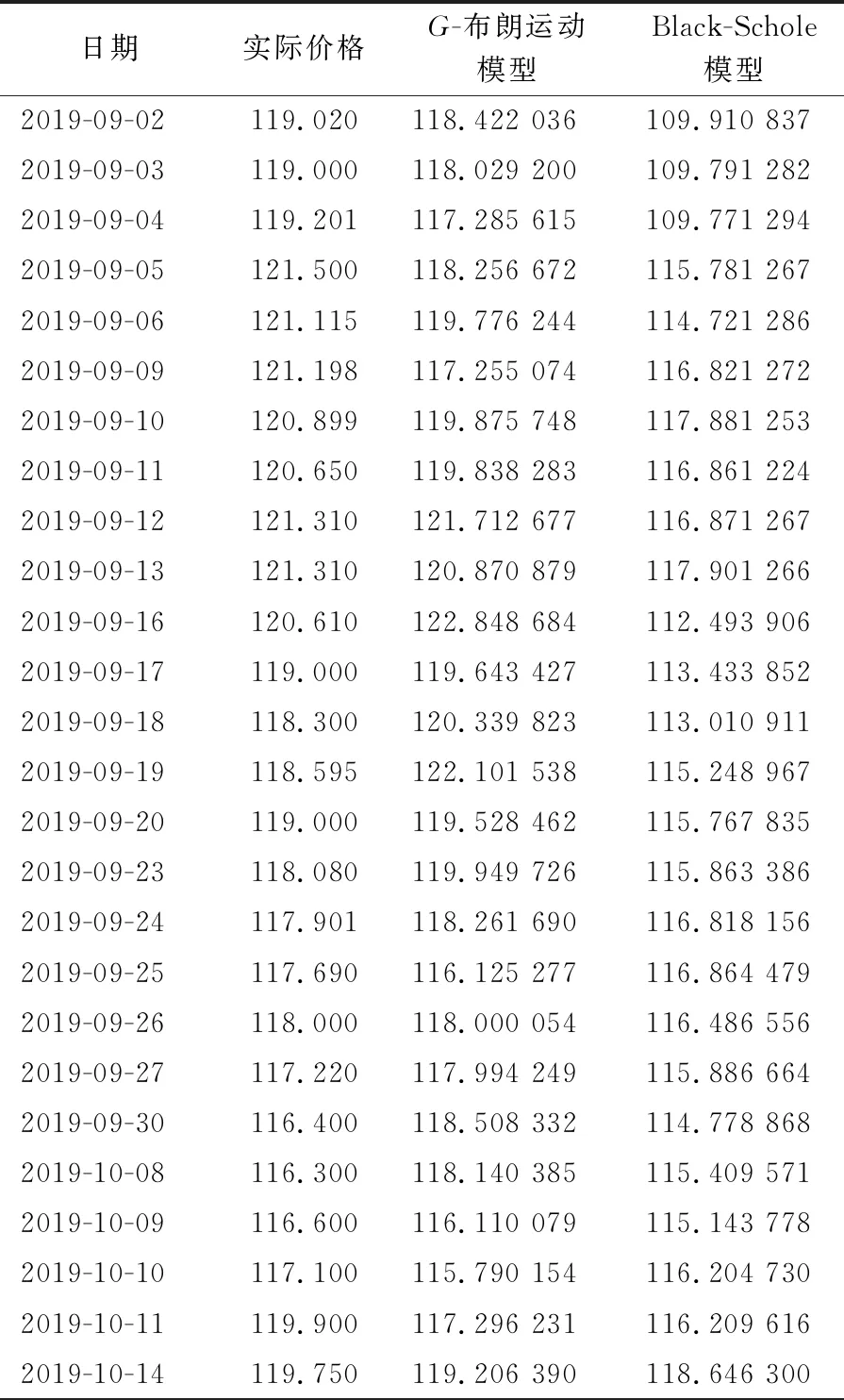
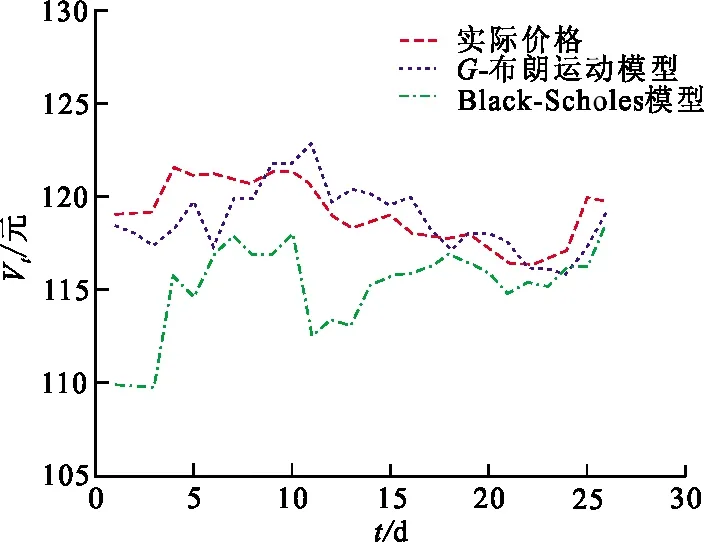
ti 假设{Bt,t≥0}是G-布朗运动,对时间区间[0,t]进行下列的划分 {ti|[0,t],0=t0 ti 令Δti=ti-ti-1,则有 (11) 其次,根据上述模拟得到的G-布朗运动的轨道{Bti,i=1,2,…,n},由定义2可以得到一条G-布朗运动二次变差的轨道。 最后,由式(3)可以模拟得到股票价格样本路径。 图 2 股票价格5条样本轨道Fig.2 5 sample tracks of stock price 基于以上股票价格轨道的模拟过程,利用蒙特卡洛法[19]进行G-布朗运动环境下可转换债券定价, 步骤如下: 1) 重复上述股票价格模拟过程m次,可得到m个股票价格到期日的值ST,1,ST,2,…,ST,m; 2) 若第i次模拟看涨期权价格为Ci=exp(-r(T-t))E[max(ST,i-K,0)],则期权价格的蒙特卡模拟值可表示为 例2 采用同样的方法重复多次,可以得到多条标的资产期权的路径图。利用例1中的数据,取r=4.27%,C=7.45,P=96.10,Q=100。利用蒙特卡洛模拟计算期权价格见表1。 表 1 不同模拟次数下的欧式看涨期权价格Tab.1 European call option price under different simulation times 由表1可以看出,当模拟次数达到1 000次以上,时期权价格逐渐趋于稳定值18.80。 选取长江证券在2018年8月31日至2019年10月14日期间每个交易日的收盘价以及长证转债在2019年8月31日至2019年10月14日每个交易日的收盘价,采用当前5年国债利率为市场无风险利率,r=4.27%,对G-布朗运动环境下的可转换债券定价进行实证分析。其中,债券期限为6年,发行面值为100元,初始转股价格为7.60元/股,债券利率分别为第1年0.2%,第2年0.4%,第3年1.0%,第4年1.5%,第5年1.8%,第6年2.0%。所用数据来源于Wind数据库及东方财富网。 4.1.1G-布朗运动环境下参数估计 根据G-布朗运动参数估计方法及实际数据,可估计模型所用到的参数如下: 进行实证分析时,采用年化波动率,即 4.1.2 Black-Scholes模型下参数估计 利用下式进行参数估计: 根据实际数据得到以下参数估计结果: 即 已知2019年8月31日股票收盘价为6.95元,即初始价格S0=6.95元,利用4.1中参数估计值及可转换债券数值模拟算法,可以分别得到G-布朗运动环境下和传统Black-Scholes模型下长证转债在2019年8月31日至2019年10月14日期间26个交易日的数值模拟价格,见表2。 基于以上数据,为了更直观的衡量G-布朗运动模型与传统Black-Scholes模型数值模拟价格与实际价格之间的差距,长证转债26个交易日的模拟价格与实际价格对比如图3所示。 表 2 可转换债券数值模拟价格Tab.2 Numerical simulation price of convertible bond 单位:元 图 3 长证转债模拟价格与实际价格对比Fig.3 Comparison of simulated and actual prices of Changzheng convertible bond 由图3可以看出,G-布朗运动数值模拟价格(单位:元)与传统Black-Scholes模型相比更加符合实际价格变动趋势,且与实际价格之间距离更小。 利用G-布朗运动模型和Black-Scholes模型下计算所得价格的均方误差和相对误差来衡量模型的优劣。均方误差及相对误差计算公式分别为 误差计算结果见表3。由表3可见,在G-布朗运动环境下得到的可转换债券价格与实际价格之间的均方误差及相对误差,均小于Black-Scholes模型,说明运用G-布朗运动模型的测量精度要高于传统Black-Scholes模型。 表 3 长证转债数值模拟价格的误差对比分析Tab.3 Comparative analysis of errors in numerical simulation price of Changzheng convertible bond 利用G-布朗运动来刻画股票价格变动,在减弱传统Black-Scholes模型波动率确定的假设基础上,研究了G-布朗运动下可转换债券定价问题并得到了定价公式。以长证转债数据进行实证分析,验证了模型的可行性,也证明了该定价方法比传统的Black-Scholes模型更加符合实际。

3.3 可转换债券定价
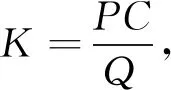

4 实证分析
4.1 参数确定
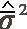

4.2 可转换债券数值模拟价格

5 结 语

