树上限制性k-node multi-multiway cut 问题的近似算法

杨 惠 娟

(昭通学院 数学与统计学院，云南 昭通 657000)

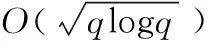
1 树上限制性k-node multi-multiway cut 问题

树上限制性k-node multi-multiway cut问题是指任意给定树T=(V,E;w)以及正整数k和顶点V的q个顶点子集构成的集合S={S1,S2,…,Sq}，对∀i∈{1,2,…,q},Si⊂V,其中w:V-S→R+,目标是求G的一个顶点子集D，使得D满足如下条件:

(1)对∀i∈{1,2,…,q},D不含Si中的点。

(2)S中至少有k个子集在G-D中不连通。

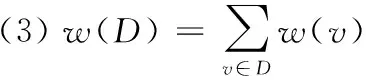
D称为限制性node multi-multiway cut。Si称为终端集，Si中的点称为终端点。根据定义要求每个Si是独立集。

若对∀i∈{1,2,…,q}，都|Si|=2，则此问题转化为限制性k-node multicut问题；若k=q=1此问题转化为限制性node multicut问题。

下面通过将k-严格顶点覆盖问题归约到此问题来说明它们具有相同的近似比。

k-严格顶点覆盖(k-SVC)是指给定一个无向图G=(V,E)及正整数k，目标是求G的一个顶点子集，使得由这个顶点子集导出的子图至少有k条边[8]。

定理1 若k-严格顶点覆盖问题存在近似值为α的多项式时间算法，则调用此算法可得到树上限制性k-node multi-multiway cut问题的近似值也为α。

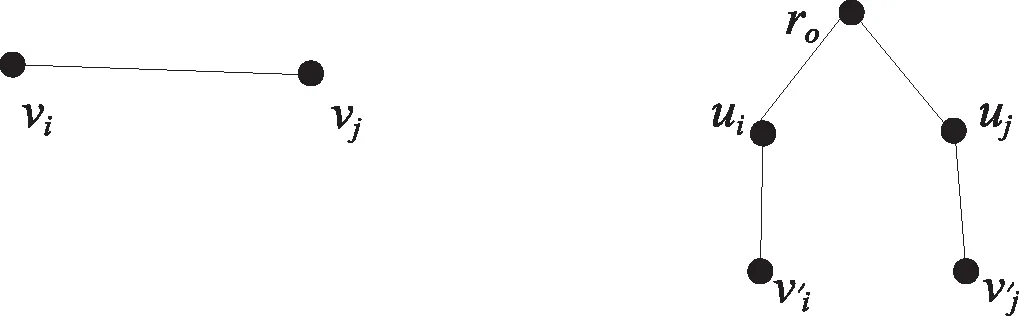
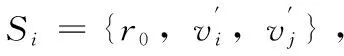
例 已知k-严格顶点覆盖(k-SVC)的实例I及按照定理的构造方式得到k-node multi-multiway cut问题的一个实例τ(I)如下：

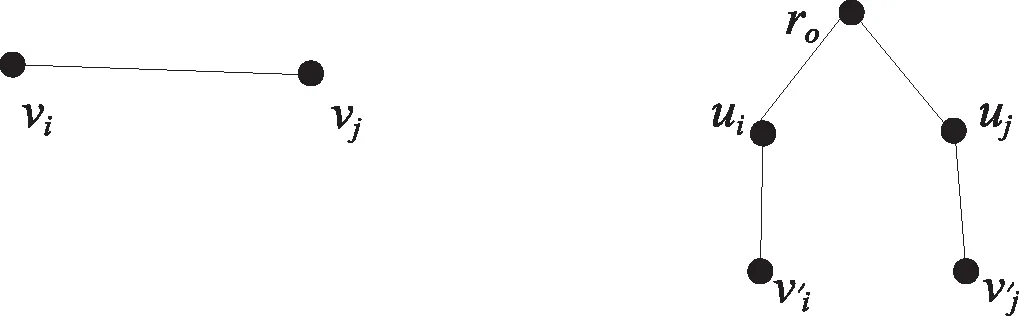
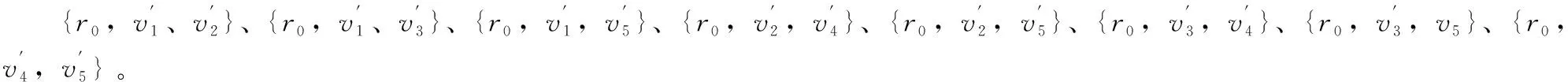
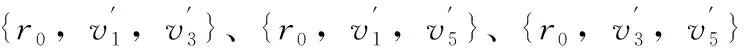
这3个终端集对应了实例I中的3条边(v1,v3)、(v1,v5)、(v3,v5)，而U={u1,u3,u5}对应了实例I中的顶点子集为V′={v1,v3,v5}，且G[V′]中恰好有3条边(v1,v3)、(v1,v5)、(v3,v5)。

2 树上限制性k-node multi-multiway cut问题的近似算法

本节主要介绍如何运用贪心策略和线性规划理论的LP-rounding技术设计问题的近似算法。

2.1 贪婪策略

另一方面，由于树上的限制性node multiway cut 问题可以用动态规划在多项式时间内求得最优解。因此为了降低近似比，将原问题分解成q个树上的限制性node multiway cut 问题进行求解，求得每一个子问题的最优解，然后按上述方式找出前k个权重最小的顶点子集，就得到原问题的一个可行解，并且此可行解的近似值为k。

2.2 LP-rounding技术

下面用0-1整数规划来描述树上的限制性k-node multi-multiway cut问题。

设D表示树上限制性k-node multi-multiway cut。变量xv∈{0,1}表示顶点v是否属于D。若xv=0表示顶点v不在D中，若xv=1表示顶点v在D中，Pi表示终端集Si中所有点之间的路集合，因为树上任意两点之间只有唯一的一条路，故|Pi|≤2|Si|，变量zi∈{0,1}用来记录终端集合Si是否断开。因此得到如下0-1整数规划，记为IP：

(1)

(2)

xv∈{0,1}

(3)

zi∈{0,1}

(4)

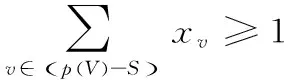
0-1整数规划的求解是NP难的，当变量数比较少时一般采用穷举法，但是当图的规模比较大时导致变量数比较多，用穷举法几乎是不可能的。

将上述0-1整数规划转换为松弛线性规划记为LP：

(5)

(6)

0≤xv≤1

(7)

0≤zi≤1

(8)

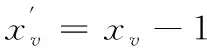
(9)

(10)

xv≥0

(11)

zi≥0

(12)

上述规划记为RLP，它的规模是多项式的，可用椭球算法[1]进行求解。设求得的最优解用向量形式表示为(x*,z*)，若(x*,z*)中的每个分量都是整数，则为原问题的最优解，若有些分量是分数的形式，那么将用LP-rounding技术把求得的分数解逐步调整为整数解。

调整方法如下：

上式与RLP的约束条件(11)矛盾。

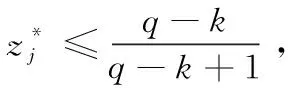
(13)

则式(13)是下列线性规划的可行解

(14)

xv≥0

(15)

上述线性规划对应的是树上限制性node multicut问题的分数解，设树上的限制性node multicut问题的最优解为OPT，调用文献[10]算法可得树上限制性node multicut的一个近似值为2的可行解x**，由式(13)得

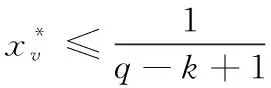
于是

(16)

设原问题的最优解为OPT1，因此满足线性规划RLP的所有约束条件是RLP的可行解而(x*,z*)是RLP的最优解，从而得到

(17)

由式(16)和式(17)得

综上所述，得如下定理：

定理2 树上限制性k-node multi-multiway cut问题具有近似值为min{2(q-k+1),k}的算法。

3 结 语

研究了限制性k-node multi-multiway cut问题限制在特殊图树上的情况，并借助树的性质及贪心策略和线性规划的LP-rounding技术设计了近似值min{2(q-k+1),k}的多项式时间算法。如何改进算法提高精确度及考虑更多特殊图上的限制性k-node multi-multiway cut问题是下一步主要的研究方向。