B-矩阵线性互补问题解的误差界的新估计式

周 平

(文山学院 数学与工程学院，云南 文山 663099)

线性互补问题LCP(A,q)是数值计算与运筹学之间相互交叉的研究领域之一，其在力学、经济学、工程学、控制论等领域具有重要应用的一类优化问题，如:接触力学问题、流体弹性动态润滑问题、空间价格问题、交通平衡问题、对策论模型及最优控制问题等[1-5]。对于给定的n阶矩阵A=(aij)∈Rn×n，n维实向量q∈Rn，LCP(A,q)的模型是指寻找解x*∈Rn，使其满足

Ax+q≥0，(Ax+q)Tx=0，x≥0。

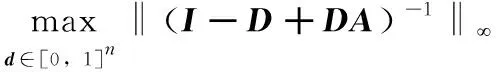
(1)

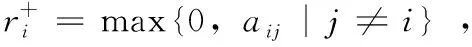
(2)

其中

2016年，李朝迁等[9]给出比(2)式更好的结果：

(3)

其中

2018年，王峰等[11]获得如下估计式：

(4)

其中

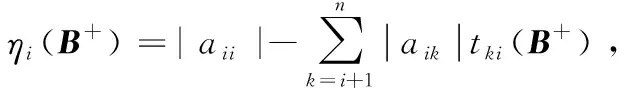
本文在文献[15]的基础上，进一步探讨了LCP(A,q)中A是B-矩阵时的误差界,给出其上界的一个新估计式，理论分析和数值例子均表明，新估计式改进了现有的一些结果。

1 符号、定义和引理

为了便于后文的探讨，先给出如下记号：

记N={1,2,…,n}]，Rn×n是全体n×n阶实矩阵构成的集合。设A=(aij)∈Rn×n，对任意的i、j、k∈N，j≠i，令

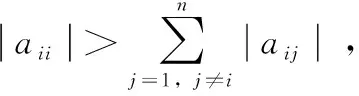
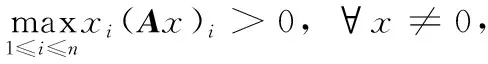
引理1[15]设A=(aij)∈Rn×n为严格对角占优M-矩阵，则

‖A-1‖

引理2[8]若γ>0,η≥0，则对任意的x∈[0,1]，有

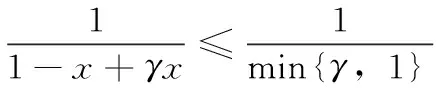
2 主要结果

定理1 如果A=(aij)∈Rn×n是B-矩阵，令A=B++C，且B+=(bij)形同式(1)，那么

(5)

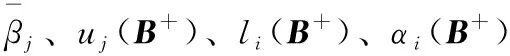
证明 设AD=I-D+DA，则

AD=I-D+D(B++C)=(I-D+DB+)+DC，

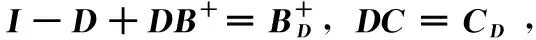
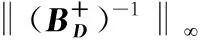
对任意的i、j、k∈N且j≠i，应用引理2和引理3得

(6)

(7)

(8)

(9)

(10)

(11)

(12)

且有

(13)

(14)

(15)

(16)

(17)

故由式(13)-式(17)得

接下来，对定理1和式(3)进行比较。

定理2 如果A=(aij)∈Rn×n是B-矩阵，令A=B++C，且B+=(bij)如(1)式定义，那么

(18)

证明 应用定理1证明中的式(6)-式(12),文献[15]中的定理2的证明以及B+的概念，知

则j

进而

所以

又注意到

综上所证知式(18)成立。本文给出的估计式和文献[11]中给出的结果不便于从理论上进行比较，但可从下面的数值例子进一步验证文中给出的定理1比文献[11]中的估计式好，提高了估计的精确度。

3 数值例子

显然，根据定理2的证明以及此例子可知，文中定理1给出的估计式优于文献[7,9,11]给出的结果，是对矩阵理论相关内容的一个有益的补充。