基于k-means++的多敏感属性t-closeness隐私保护
吴荣士,叶欣欣,许林涛,裴成飞
(安徽理工大学 计算机科学与工程学院,安徽 淮南 232001)
在大数据时代,保护个人隐私信息至关重要。通常,生成适合发布的匿名数据集需要在披露风险和信息损失之间找到权衡。k匿名[1-2]是一种较成熟的隐私模型,可以防止身份泄露,但是不能防止属性泄露。基于k匿名衍生出许多扩展模型,如(α,k)-anonymity[3]、l-diversity[4]、(k,l)-diversity[5]、t-closeness[6]等。考虑到严格的隐私保证,本文重点关注t-closeness模型。Wang Rong等[7]提出了一种基于Equi-sized FCM聚类方法的多敏感属性t-closeness算法,该算法在等价类生成的过程中没有添加t-closeness限制,不能保证生成的等价类满足t-closeness, 从而使得最后生成的等价类可能包含过多数量的记录,降低了数据效用。 基于此问题,本文基于k-means++聚类,在等价类生成的过程中添加t-closeness限制,使得生成的等价类尽可能满足t-closeness,从而能够在保护隐私的前提下提高数据效用。
1 基本概念
假设数据集D={QI1,QI2,…,QIn,SA1,SA2,…,SAm}有N条记录,每条记录ri(1≤i≤N)包括n个准标识属性QI1、QI2、…、QIn和m个敏感属性SA1、SA2、…、SAm,准标识属性的域为Dom(QIi)(1≤i≤n),敏感属性的域为Dom(QIi)(1≤i≤n),ri[A]表示记录ri(1≤i≤N)在属性A上的取值。
1.1 k匿名
如果攻击者能够确定匿名数据集中的某条记录所对应的用户身份时,就可以重新识别这条记录。在这种情况下,攻击者可以将重新识别的记录中的敏感属性值与用户的身份相关联,从而获取用户的隐私。k匿名就是为了限制攻击者重新识别用户身份的能力。
定义1 (k匿名)[1]:对于数据集D中的准标识属性,其属性值的每个组合在共享该组合的数据集D中存在至少k条记录,则称数据集D满足整数为k(k≥2)的k匿名。
在k匿名数据集中,每个用户的身份可被链接到至少k条记录。因此,基于准标识属性,攻击者至多有1/k的概率能够正确的识别出用户的身份。
1.2 t-closeness
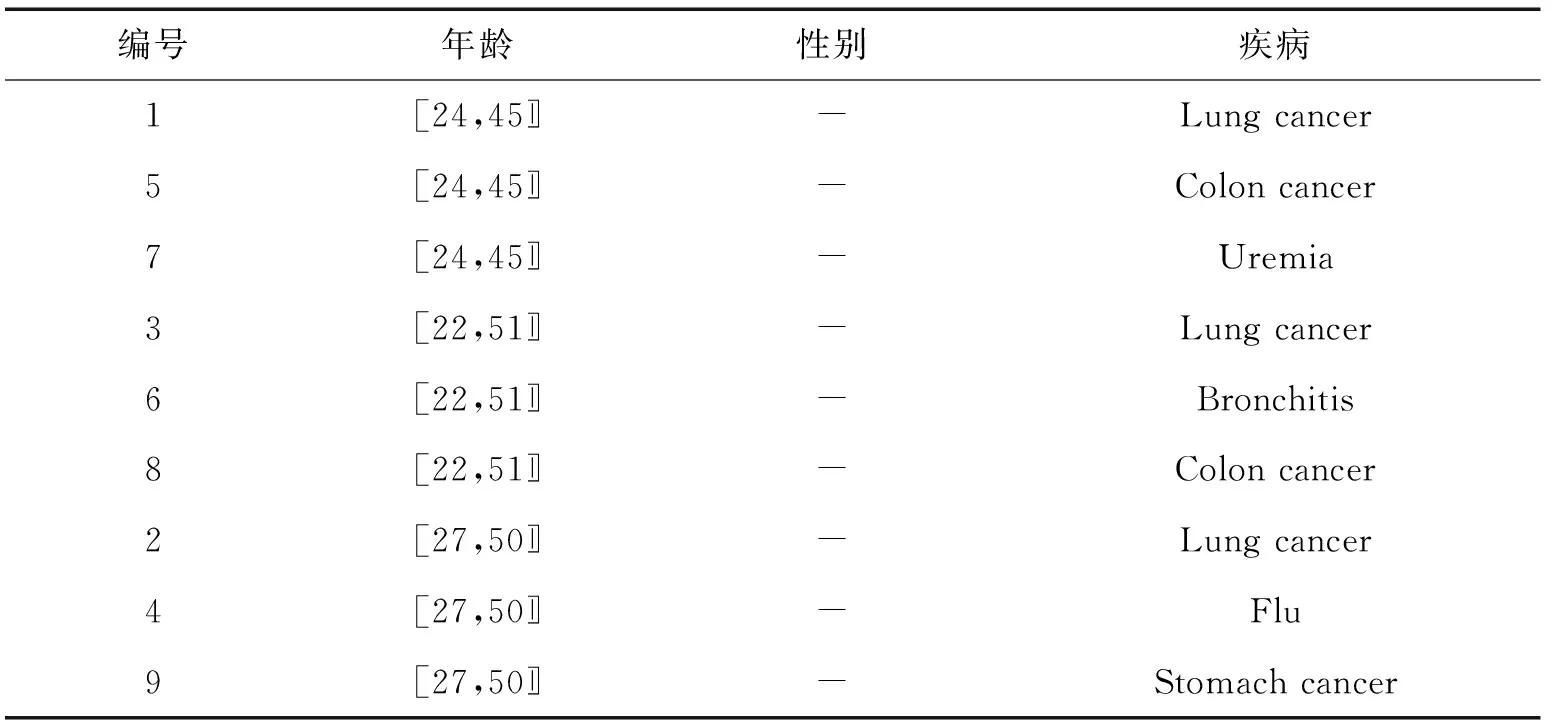
k匿名性可以防止身份泄露,但是不能够防止属性泄露。当等价类中的敏感属性值的可变性太低时,容易发生属性泄露。针对这一问题,目前已经提出了一些k匿名的扩展方法用于限制属性泄露,t-closeness就是其中之一。t-closeness具有严格的隐私保证,它要求每个等价类内的敏感属性的分布与其在整个数据集中的分布相似。例如:某医疗机构的原始数据集如表1所示,基于表1的满足0.33-closeness的匿名化数据如表2所示。本文主要基于t-closeness进行讨论。
定义2(t-closeness)[6]:对于数据集D中的某个等价类,其敏感属性在类内的分布与在整个数据集上的分布距离不超过阈值t, 则称该等价类满足t-closeness,如果数据集中的所有等价类均满足t-closeness,则称D满足t-closeness。
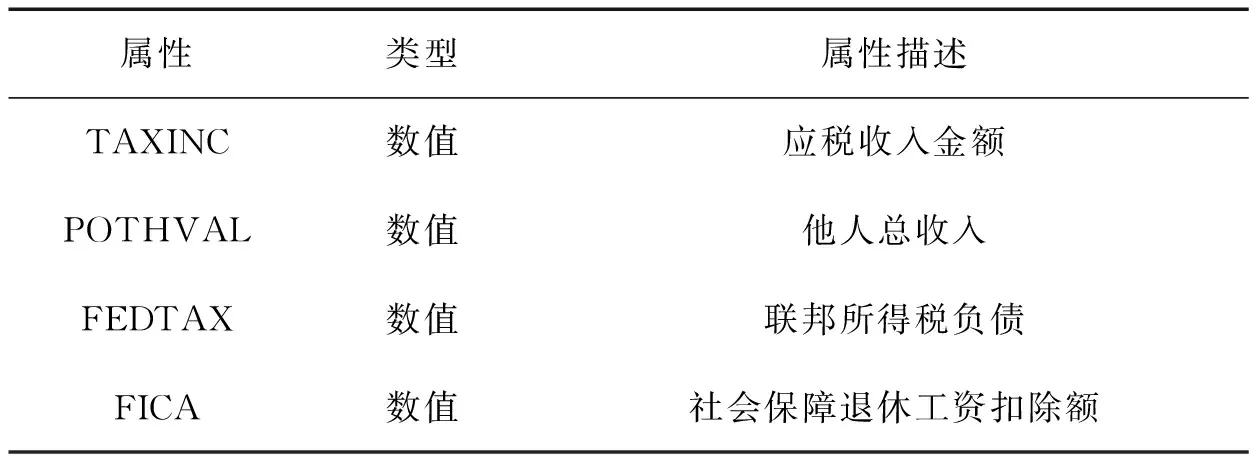
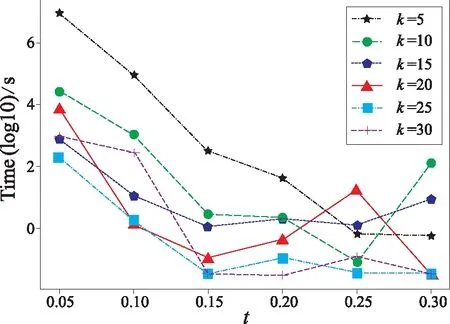
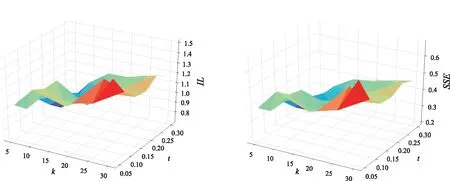
t-closeness中常用于求分布之间距离的方法是陆地移动距离(EMD)[8],EMD(P,Q) 通过移动概率质量来度量将一个分布P转换成另一个分布Q的成本。EMD计算为把箱子P移动到箱子Q所需的最小移动成本,它取决于移动的质量以及移动的距离。对于数值属性,两个箱子之间的距离与它们之间箱子的数量有关。设数值属性取值为{a1,a2,…,am},且i (1) 表1 某医疗机构原始数据 表2 基于表1满足0.33-closeness的匿名化数据 本文使用两种方法来度量匿名化前后数据的损失,一种是概化损失度量(generalized loss metric)[9-11],记QI= {QI1,QI2,…QIn}为数据集D的标识符属性集。对于数值属性,设QIi在D中的域为[L,H],a为QIi中的一个属性值,a概化后的值范围为[La,Ha],则属性值a信息损失被定义为 (2) 那么D中的一条记录rD匿名化后的信息损失为 (3) 数据集D匿名化后的信息损失为 (4) 平方误差总和(SSE)是另一种常用的信息损失量度方法,适合度量通过k匿名微聚集创建等价类的效用。本文中,SSE定义为匿名化前后属性值损失的平方和: (5) 式中:N为D中记录的条数;n为准标识符属性的个数。 现有的关于t-closeness的工作大多数仅考虑单敏感属性,而现实生活中敏感属性往往有多个。Wang等提出了一个关于多敏感属性的t-closeness定义,该定义分别考虑每个敏感属性的分布,然后取最大接近度,本文仍采用这种定义方式。 定义3 (多敏感属性t-closeness)[7]:记EC={QI1,QI2,…,QIn,SA1,SA2,…,SAm}为多敏感属性数据集D中的一个等价类, 敏感属性SAi(i=1,2,…,m)在EC中的分布与在D中的分布距离为ti(i=1,2,…,m),如果max(t1,t2,…,tm) ≤t,则该等价类满足t-closeness,如果D中的所有等价类均满足t-closeness,则认为D满足t-closeness。 生成满足t-closeness的数据集本质上是一个优化问题,即必须找到满足t-closeness的最优概化。我们提出了一个基于k-means++聚类的多敏感属性t-closeness算法,该算法由4个部分组成。第1个过程是聚类,如算法1中的行(1)所示,使用k-means++算法生成一个基于多敏感属性的k个分组,本文仅考虑数值属性,因此采用欧式距离来计算两条记录之间的距离,即对于D中的任意两条记录r1(QI11,QI12,…,QI1n,SA11,SA12,…,SA1m)和r2(QI21,QI22,…,QI2n,SA21,SA22,…,SA2m),r1与r2之间基于QI属性和SA属性的距离分别为 (6) (7) 第2个过程是一个生成等价类的过程,根据第1个过程产生的基于多敏感属性的k个分组, 循环地从每个分组中抽取一条记录组成大小为k的等价类,然后判断该等价类是否满足t-closeness,如果不满足,则从剩余的记录中选取一条距离等价类最近的记录替换掉等价类中的某条记录以使得等价类最接近t-closeness,重复上述步骤,直到所有等价类均被选出来,如算法1中行(2)-行(27)所示。 算法1 基于k-means++聚类的多敏感属性t-closeness算法 输入: D:原始数据集,k:k匿名水平,t:t-closeness水平 输出: 满足k匿名和t-closeness的数据集C′ (1)利用公式(7)对D进行k-means++聚类,得到k个分组C={C1,C2,…,Ck} (2)初始化C′ = ∅; (3)whileC≠ ∅ andC中的记录条数大于等于2k (4)初始化等价类EC=∅ (5)r=C1中随机选取一条记录;EC=EC∪ {r};C1=C1 (6)while |EC| (7)分别从2~k个分组中选取一条与r最近的记录,如果2~k个分组均为空,则从第1个分组中选取 只要保证路面的平整、清洁,同步碎石封层技术才能够正常进行。因为同步碎石封层技术要想对道路养护的效果好,就必须在平整的里面上进行操作,只要这样才能保证与地面充分接触,养护效果好。如若地面不平整或地面灰尘多,清洁度差,沥青与颗粒性碎石和地面的粘合程度收到影响,使得同步碎石封层技术的效果就大大降低,质量大打折扣,并且不利于施工完成后期对该整修路段的监修和养护工作的开展。因此,道路平整且整洁是该技术正常进行的基础。 (8)end while (9)D′ =C中所有剩余记录的集合 (10)r1=EC的质心(基于QI属性) (11)whileEMD(EC,D) >tandD′ ≠ ∅ do (12)y=D′ 中与r1最近的记录 (13)y0=EC中使得EMD(EC∪{y} {y0},D) (14)ifEMD(EC∪{y} {y0},D) (15)EC=EC∪{y} {y0} (16)C=C/y//将y从C中对应的分组中删除 (17)C=C∪y0// 将y0加入C中对应的分组中 (18)r1=EC的簇心(基于QI属性) (19)end if (20)D′=D′ {y} (21)end while (22)C′=C′∪EC (23)end while (24) ifC≠ ∅ then (25)EC=C中剩余的记录条数 (26)C′ =C′∪EC (27) end if (28)whileEMD(C′,D) >tdo (29)C=C′中使得EMD(C,D)最大的等价类 (30)C0=C′中离C最近的等价类 (31)将C与C0合并 (32)end while (33)foreachECinC′: (34)用QI属性在EC中的取值范围来概化该属性值 (35)returnC′ 第3个过程是一个归并过程,判断第2个过程中产生的等价类簇与原始数据集在敏感属性上的分布是否满足t-closeness。如果不满足,则在等价类簇中寻找与原始数据集敏感属性分布距离最大的等价类,并将其与距其质心最近的等价类合并,循环迭代类簇中的所有等价类,直到所有等价类均满足t-closeness,如算法1中行(28)-行(32)所示。第4个过程是概化,对于第3个过程产生的等价类簇中的每个等价类,用属性在该等价类中的取值范围来概化具体的属性值,最终生成一个符合k匿名t-closeness的匿名化数据集,如算法1中行(33)-行(34)所示。 使用人口普查数据集Census作为评估数据,该数据集通常用于测试隐私保护方法,其中包含1 080条具有数字属性的记录,共有13个属性。将TAXINC和POTHVAL设为为准标识符属性,并将FEDTAX和FICA设为敏感属性,属性的描述如表3所示。算法的运行环境为jdk1.8.0_212,Intel Core i5 2.6GHz,8GB RAM Win10操作系统。 表3 实验中采用的属性 对k和t取不同的值,从而获得了一系列的实验结果。k的值在5到30之间,t的取值范围为[0.05,0.30]。为了使信息丢失最小化,所有等价类的大小越接近k越好。考虑到k-means++聚类算法初始簇心的随机性对聚类结果的影响,每组取值重复实验50次,取最好结果。等价类的大小随着k值的增加而变大如表4所示,对于同一个k值,t值越小,即隐私保护水平越高,等价类的平均尺寸就越大,因而信息损失就越大。 表4 k和t取不同值时等价类的最小尺寸、平均尺寸 评估的第2部分着重于测量算法在数据集上的测试时间。k、t取不同值时算法的执行时间如图1所示,t越大,即隐私保护程度越低,算法的运行时间越小,对于Census数据集,算法的执行时间在t= 0.15前后相差较大,并且在t=0.15之前,执行时间受t的影响较大,t=0.15之后,执行时间趋于平缓;另一方面,k越小,执行时间越长,这是因为k越小,每个等价类中包含的记录条数就越少,生成满足t-closeness的等价类需要迭代计算EMD的次数越多,因而执行时间越长。 图1 k、t取不同值时算法运行时间 评估的第3部分着重于匿名化前后信息的损失,采用上文提到的两种度量方法,图2表示的是k、t取不同值时的概化损失(IL),图3表示的是k、t取不同值时的平方误差总和(SSE)。t越小,信息损失越大,即隐私保护程度越高;另一方面,在同等隐私保护程度下,等价类的大小越大,即k越大,误差越大,这是因为k越大,等价类中包含的记录条数越多,准标识属性的概化范围变大,从而导致误差变大。这也是基于准标识属性聚类和基于敏感属性聚类的一个区别。 图2 k、t取不同值时的信息损失IL 图3 k、t取不同值时的平方误差和SSE 针对大多数有关t-closeness研究未考虑到多敏感属性的问题,提出了一种基于k-means++聚类的多敏感属性t-closeness算法,使用k-means++聚类算法基于多敏感属性对原始数据集进行分组,然后从每个分组中选取一条或多条记录组成等价类,并计算其接近度,如果不满足t-closeness,则迭代地从剩余的未分组的记录中选取记录更新等价类,直至其满足t-closeness或接近度最小。实验表明本方法具有良好的效果。然而,本文算法仍有不完美的地方,为使得所有的等价类尽量满足t-closeness,在生成等价类的过程中不断计算EMD,计算复杂性高;另一方面,在计算EMD时,单独考虑每个敏感属性的分布,而没有考虑到多敏感属性的联合分布,并且没有考虑到多个敏感属性之间的关系。这些问题将在未来的工作中进一步研究。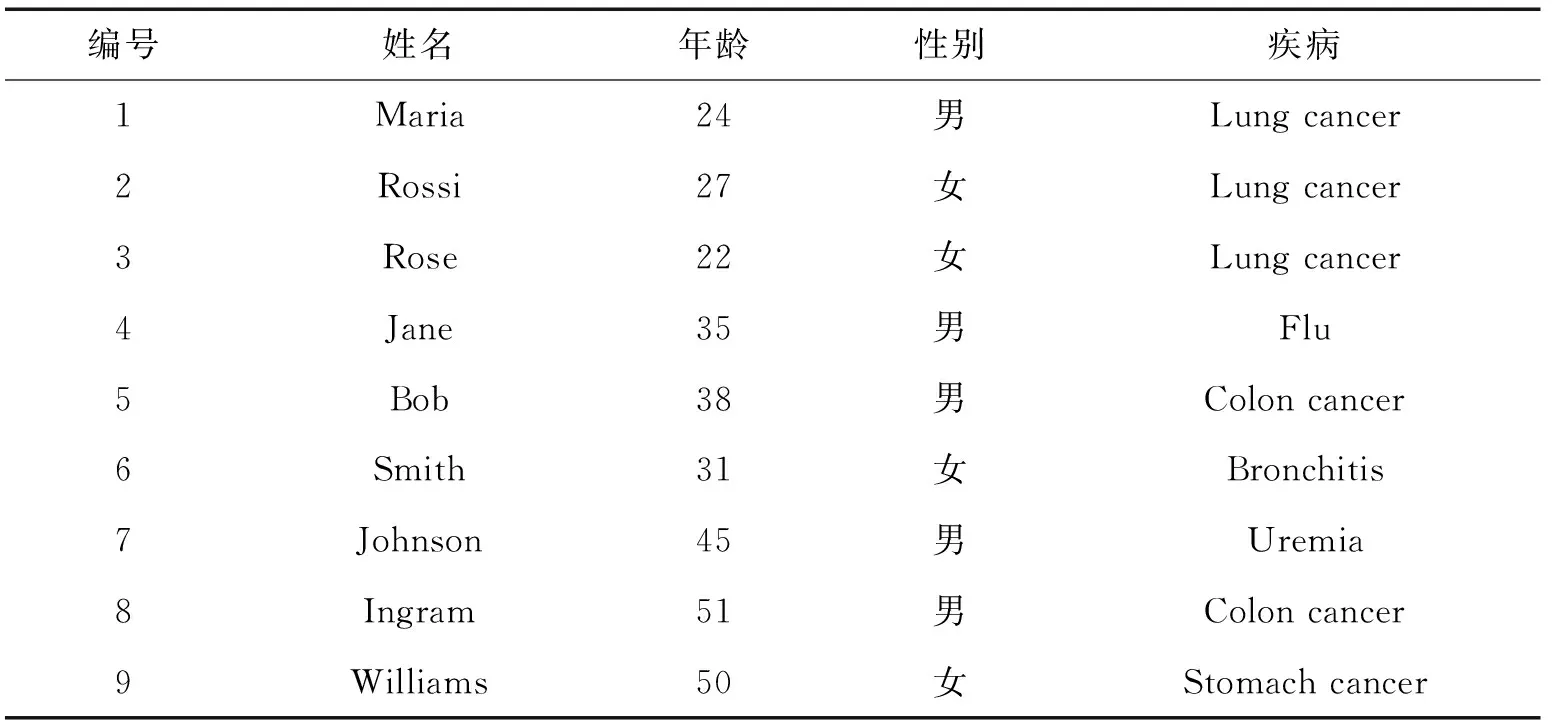
1.3 信息损失度量
2 多敏感属性的t-closeness隐私保护算法
2.1 多敏感属性t-closeness
2.2 基于k-means++聚类的多敏感属性t-closeness算法
3 实验评估
3.1 等价类大小

3.2 运行时间
3.3 信息损失
4 结 语

