在生活情境和操作体验中，构建有效的数学模型

温容

摘要：在小学数学“图形的运动”的教学中，教师通过创设学生熟悉的生活情境，提供大量的生活图片，帮助学生建立数学表象。然后通过动手操作逐步帮助学生构建有效的数学模型，通过建模教学，可以加深学生对数学知识和方法的理解和掌握，调整学生的知识结构，深化知识层次。

关键词：生活情境 动手操作 有效   数学模型

义务教育课程标准提出：数学教学要在呈现作为知识与技能的数学结果的同时，重视学生已有的经验，让学生体验从实际背景中抽象出数学问题、构建数学模型、得到结果、解决问题的过程。从这个角度讲，数学模型是数学学习中不可或缺的元素。数学模型不仅为数学表达和交流提供有效途径，也为解决现实问题提供重要工具，可以帮助学生准确、清晰地认识、理解数学的意义。在小学数学教学活动中，教师应采取有效措施，加强数学建模思想的渗透，提高学生的学习兴趣，培养学生用数学意识以及分析和解决实际问题的能力。

通过认真研读《数学课程标准》对北师版小学数学三年级“图形的运动”内容的解读，我对本单元在编排上的特点和变化理解如下：第一，结合生活经验和分类活动，初步感受平移和旋转现象，直观体会它们的特点;第二，结合在方格纸上平移物品的操作活动，体会平移运动的过程。整个小学阶段“图形的运动”内容的编排特点旨让学生积累感性认识，形成初步表象，能识别和会画图。下面，以“平移和旋转”一课教学为例，谈谈如何引导学生在解决实际问题过程中构建有效的数学模型。

一、创设生活情境，建立数学表象

数学来源于生活，生活中处处有数学。在备课时，教师充分考虑了学生的年龄特点和认知发展水平，因而在教学中我结合学生的实际生活中熟悉和喜爱的事物运动，如：缆车、升国旗、小火车、各式各样游的小鱼、秋千、螺旋桨、钟摆等让学生用眼观察、动手操作、亲身体验等步骤，把抽象的概念变为看得到摸得着的现象，使学生认识、感知平移和旋转现象。让学生在观察中去比较和体会平移和旋转的特点，让学生在数学活动中学会数学知识。

二、在动手操作中，构建有效的数学模型

在“图形与几何”的教学中，教师要尽可能地创造条件让学生参加动手操作活动。如果在“图形与几何”教学中仅靠老师的操作演示，没有学生的亲自动手操作，学生获得的知识还是很肤浅的。只有让每个学生都参加动手实践操作中来，运用多种感官参加学习活动，才可能使学生获得比较充分的感知，才便于储存和提取数学信息。在“图形与几何”教学中，教师要提供更多的机会让学生动手操作，使学生在动手操作的活动中发展学习兴趣，获取知识。

教学片断：

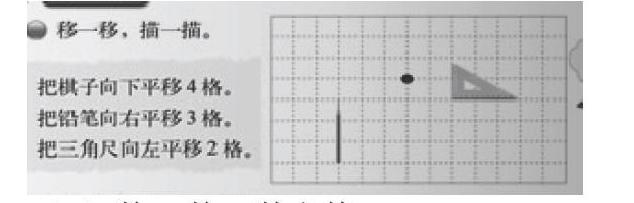
1.多媒体出示课本的主题图。

（1）数一数：数方格

先把棋子向下平移4格，描下来。（请同学们，在格子图上找出棋子要向什么方向平移了几个格子？你是怎么看的？同桌讨论。汇报交流。）

（可以看某一个点，棋子移过了几格，就平移了几格，就可以找到棋子所到的位置。）（多媒体演示，点住棋子的一点闪亮，往前移。）

（2） 描一描：同学都会数方格了，现在就让我们来试一试在方格图上画出棋子来吧。

师接着引导学生把铅笔向右平移3格，描下来。

先提醒学生在移前要注意判断向哪个方向移动，移动几格。再让学生讨论怎样画？（请学生上台操作先找到铅笔的两个顶点，然后分别向右平移3格，再将两个点连接。多媒体演示两个点移动，再连接）

（3）再把三角尺向左平移2格，描下来。

移动三角尺：指导学生以三角形中的某一点（如顶点）为标准，观察它的平移方向和位置，然后判断最终位置并画出来。师点明：观察一个图形的平移过程，只需要观察图形上任意一点的平移过程。画出三角尺向左平移2格后的图形。（学生独立画在方格本上）

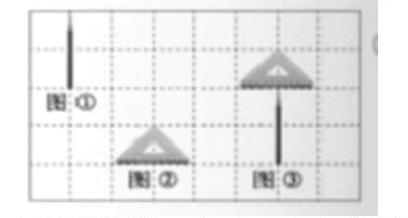
2.說一说，铅笔和三角尺是怎样才能平移到图3的位置？

平移铅笔：先向右平移5格，再向下平移2格;

也可以先向下平移2格再想右平移5格。

平移三角尺：先向右平移3格，再向上平移2格;

也可以先向上平移2格，再想右平移3格。

追问：你是如何找出平移几格后图形的位置的？

生：可以看三角形的三个顶点。看看这几个具体的点平移了几格。

在教学中，教师要提供更多的机会让学生动手操作，使学生在动手操作的活动中发展学习兴趣，获取知识。通过引导观察，让学生描述自己平移的过程，老师放手让学生数一数，移一移，描一描，说一说，从而调动学生的多种感官的参与，而不是空洞地告诉学生这就是平移的概念，为学生构建了平移的数学模型。

构建数学模型是一个综合性的过程，是数学能力和其他各种能力协同发展的过程。在数学教学过程中进行数学建模思想的渗透，不仅可以使学生体会到数学并非只是一门抽象的学科，而且可以使学生感觉到利用数学建模的思想结合数学方法解决实际问题的妙处，进而对数学产生更大的兴趣。同时，在建模的过程中，学生经历了观察、操作、实践、总结等一系列数学活动，经历了知识的形成和发展过程，培养了学生应用数学的意识和自主、合作、探索、创新的精神，学生数学思维的灵活性，深刻性均得到了锻炼与提高，形成了学生良好的思维习惯和用数学的能力。为学生的终身学习、可持续发展奠定基础。

参考文献：

[1]吴正宪，王彦伟.图形与几何若干内容分析——《义务教育数学课程标准（2011年版）》解析之八[J]. 小学数学教育，2012（Z2）.

[2]崔银艳.浅谈图形与几何教学中空间观念的培养[J].新课程学习（下），2011（11）.