带恶化和综合学习效应的成组排序问题研究

孙 丽, 马卫民

(上海电机学院 商学院,上海 201306)

0 引言

随着工业生产的发展，工件的加工时间通常会受到很多外部因素的影响而使工件实际加工时间发生改变。在排序中，这种工件加工时间的变化总的分为两类：一类是工件的实际加工时间比其正常加工时间短，这类因素在排序中被称为学习效应；另一类是工件的实际加工时间比其正常加工时间长，这类因素被称为恶化效应。加工时间变化的排序问题是近年来的研究热点之一。Przybylski[1]研究了基于积分学习效果的并行机排序问题。Bai等[2]讨论了带工件到达时间和学习效应的流水作业排序，对问题给出了分枝定界算法。Ji等[3]研究了一类带DeJong学习效应的单机和平行机排序，对问题给出了最优算法。

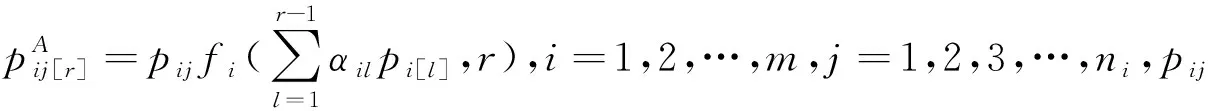
1 模型分析

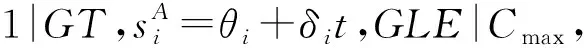
证明组内工件的排序按常用的相邻工件交换法容易得证，这里从略；

Ci[1](S1)=θi+(1+δi)t+pi[1]

…

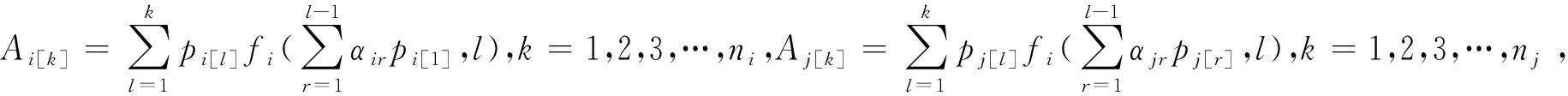
所以，

Ci[ni](S1)=θi+(1+δi)t+Ai[ni],

Cj[1](S1)=θj+(1+δj)Ci[ni](S1)+pj[1],

…

Cj[nj](S1)=θj+(1+δj)(θi+(1+δi)t+Ai[ni])+Aj[nj]

(1)

…

…

(2)

公式(1)和(2)作差可得:

=θi+(1+δi)(θj+(1+δj)t+Aj[nj])+

Ai[ni]-(θj+(1+δj)·

(θi+(1+δi)t+Ai[ni])+Aj[nj])

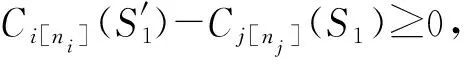
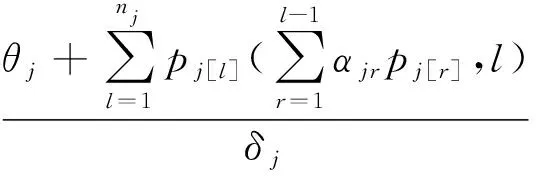
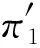
算法1

步骤1每组内工件按正常加工时间pij非减排列，j=1,2,…,n。

步骤2对每个工件组计算

组间按μ(Gi)非减排列，i=1,2,…,m。

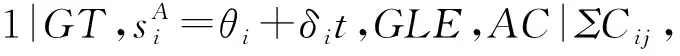
证明组内工件的排序按常用的相邻工件交换法容易得证，这里从略；

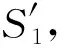
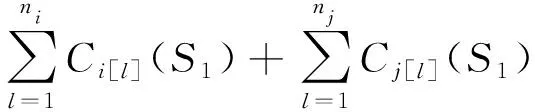
由定理1，可得:

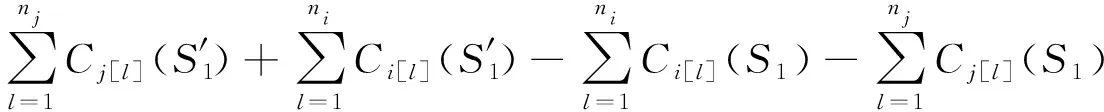
=(ni(1+δi)δj-nj(1+δj)δi)t+ni(1+δi)(θj+Aj[nj])-nj(1+δj)(θj+Ai[ni])

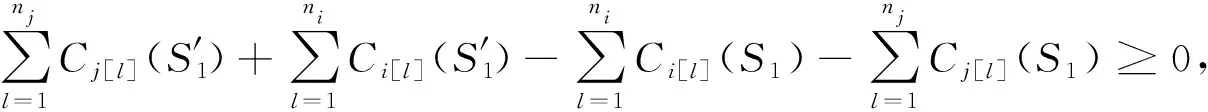
ni(1+δi)δj-nj(1+δj)δi≥0

(3)

ni(1+δi)(θj+Aj[nj])-nj(1+δj)(θi+Ai[ni])≥0

(4)

因此，如果λ(Gi)和η(Gi)有一致关系，在最优排序中，组间排序按λ(Gi)非减排列。

算法2

步骤1组内工件按正常加工时间pij非减排列，j=1,2,…,ni，即pi[1]≤pi[2]≤pi[3]≤…≤pi[ni],i=1,2,3,…,m,(SPT规则)。

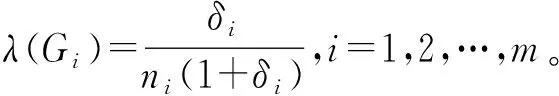
步骤3组间按λ(G[i])不减排列，即λ(G[1])≤λ(G[2])≤λ(G[3])≤…≤λ(G[m])。

显然,算法2的计算复杂性是O(nlogn)。

2 算例分析

方法：

根据算法1， 我们按照如下步骤解决:

步骤1对于工件组G1， 最优的工件序是J11→J12；

对于工件组G2， 最优的工件序是J22→J21→J23；

对于工件组G3,最优的工件序是J31。

步骤2计算可得:μ(G1)=120.16，μ(G2)=75.97，μ(G3)=18.75。易知μ(G3)<μ(G2)<μ(G1)。因此， 最优的组序是：G3→G2→G1，总的最优排序是：[J31]→[J22→J21→J23]→[J11→J12]；各工件的完工时间是：G31=15，G22=27.5，C21=33.658,C21=33.658,G23=42.291，G11=51.5201，G12=58.5361；时间表长是：Cmax=58.5361。

对于问题1|GT,si=θi+δit,GLE|ΣCj，仍然假设第一个工件组开始安装时间是t=0。

方法：

根据算法2, 我们按照如下步骤解决:

步骤1对于工件组G1， 最优的工件序是J11→J12；

对于工件组G2， 最优的工件序是J22→J21→J23；

对于工件组G3， 最优的工件序是J31→J32。

步骤2计算可得:

λ(G1)=0.0455，λ(G2)=0.077，λ(G3)=0.444，η(G1)=5.462，η(G2)=5.844，η(G3)=8.333，易知,λ(G1)<λ(G2)<λ(G3)，η(G1)<η(G2)<η(G3)。因此，最优的组序：G1→G2→G3，总的最优排序是[J11→J12]→[J22→J21→J23]→[J31]，各工件完工时间是G11=5，G12=12.016，G22=23.6208，G21=29.7788，G23=38.4118，G31=84.1412，总完工时间是：ΣCj=5+12.016+23.6208+29.7788+38.4118+84.1412=192.9686。

3 结论

本文讨论了一类综合学习效应下的成组排序问题。对于极小化时间表长问题给出多项式算法，并证明了具有一致关系的极小化总完工时间问题也是多项式可解的。