基于模糊测度与累积前景理论的区间二型模糊多准则决策方法
刘 超,汤国林,刘培德
(1.北京工业大学 经济与管理学院,北京 100124; 2.北京现代制造业发展基地,北京 100124; 3.山东财经大学 管理科学与工程学院,山东 济南 250014)
0 引言
Zadeh[1]定义的一型模糊集,是刻画客观事物不确定性的重要工具之一。一型模糊集的隶属度是精确值,无法解决隶属度不确定的问题。因此,Zadeh[2]对一型模糊集进行拓展,定义了二型模糊集,其隶属度本质是一型模糊集,能够更加灵活和准确地处理不确定性问题。然而,一般形式的二型模糊集存在难以理解且计算比较复杂等缺点。为此,区间二型模糊集[3]作为二型模糊集的特例,由于其能较好地描述不确定性以及计算相对简单而受到学者的青睐,并已应用于图像分割[4]、人力资源管理[5]、投资项目评估[6]、绿色供应商选择[7]等实际问题中。目前,关于区间二型模糊信息的研究成果主要分为以下三类:1) 区间二型模糊信息的测度理论,如距离测度[7]、相似性测度[8]、熵[9]等。2) 区间二型模糊信息的决策方法,如拓展的TODIM方法[7]、拓展的VIKOR方法[10]、拓展的DEMATEL方法[11]、拓展的PROMETHEE方法[12]等。3)区间二型模糊信息的融合理论,如广义梯形区间二型加权平均(GTIT2FWA)算子[13]、区间二型加权幂平均(IT2WPA)算子[14]、区间二型模糊加权几何Bonferroni平均(IT2FWGBN)算子[15]、加权匀称三角区间二型模糊Hamy平均(WSTIT2FHM)算子[16]、优先区间二型模糊集成(PIT2FA)算子[17]等。
区间二型模糊信息的测度理论在区间二型模糊决策理论中占据着基础性地位,它不仅可以应用于决策分析、模式识别、机器学习等实际问题,而且也是拓展的TODIM方法[7]、拓展的VIKOR方法[10]、拓展的PROMETHEE方法[12]等方法的基础。区间二型模糊信息的决策方法可以有效利用决策信息对方案集进行排序。区间二型模糊信息的融合理论不仅可以对方案集进行排序,还可以计算不同方案综合值的数量大小。因此,在处理多准则决策问题方面,区间二型模糊信息的融合理论比区间二型模糊信息的决策方法更具有优势。在区间二型模糊信息的融合理论中,GTIT2FWA算子[13]基于属性之间相互独立的假设,无法处理属性之间存在相互关系的多准则决策问题。IT2WPA算子[14]、IT2FWGBN算子[15]、WSTIT2FHM算子[16]、PIT2FA算子[17]可以考虑准则之间的相互关系,其中,IT2WPA算子[14]考虑了集成数据之间相互支撑程度对权重的影响,IT2FWGBN算子[15]反映了两两集成数据之间存在的相互关系,WSTIT2FHM算子[16]考虑了多个集成数据之间存在的相互关系,PIT2FAO算子[17]反映了准则之间存在的优先关系。
然而,目前有关区间二型模糊信息的融合理论的研究仍存在两个缺陷。一方面,现有的区间二型模糊信息的融合理论基于准则之间相互独立或存在简单相互关系的假设。实际问题的决策准则之间可能存在复杂的不同程度的关联关系,如互补关联、冗余关联以及独立等[18~23]。例如,决策者依据地理位置、价格、硬件设施等指标对房屋进行选择时,会出现这样的情形:地理位置、硬件设施与价格分别存在关联关系,而地理位置与硬件设施是相互独立的。另一方面,现有的区间二型模糊信息的融合理论基于传统的期望效用理论,该理论假设决策专家是完全理性的。在实际决策过程中,决策专家面对诸多不确定因素时,他的判断和行为受到个人习惯偏好及风险态度等的影响,很难做到绝对理性,而是有限理性的[24~28]。例如,决策者在房屋的选择过程中,可能对房屋的地理位置等指标有一定的期望要求,对高于期望所带来的对收益与低于期望所导致的损失具有不同的风险态度。
Sugeno[18]定义的模糊测度能够度量准则之间的互补关联、冗余关联以及偏好间的关联[19],是解决复杂关联多准则决策问题的一种有效方法。基于模糊测度的Choquet积分算子是一种可以有效集成关联准则评估值的集成算子。针对准则之间具有关联关系的区间值直觉犹豫模糊多准则决策问题,Joshi与Kumar[20]提出了区间值直觉犹豫模糊Choquet积分算子。Xu[21]和Tan等[22]分别定义了直觉模糊关联平均算子和直觉模糊Choquet积分算子,并给出了相应的决策方法。虽然,Joshi与Kumar[20],Xu[21],Tan等[22]所定义的算子能够反映准则本身或者所处位置的重要程度,以及考虑准则之间或者所处位置的关联关系。但是,这些算子只能考虑临近准则组合之间的关联关系。为了全面考虑准则之间存在的复杂关联关系,孟凡永等[23]研究了基于三角模糊数的广义λ-Shapley Choquet积分算子及其在工程项目投资方案评价问题中的应用。因此,拟将Choquet积分算子与广义Shapley值拓展到区间二型模糊集,提出Shapley区间二型模糊Choquet积分(SIT2FC)算子,以全面考虑准则间存在的复杂关联关系。
Kahneman和Tversky[24]提出的前景理论可以较好地描述参照点依赖、风险偏好逆转以及损失规避等决策专家行为特征,更加符合人们的实际决策行为,解释很多期望效用理论所不能解释的现象。后来,Tversky和Kahneman[25]对前景理论进行了修正,结合累积泛函提出了累积前景理论,较好地解决了随机占优及对多个结果的处理问题。在累积前景理论中,参照点的选取非常重要,直接影响着决策结果,现有的参照点选取主要有正理想点、平均值点、中值点、预期值、零点或负理想点。这些参照点的设置方法是从单一角度出发,无法体现决策的复杂性特征。对此,李欢等[26]同时引入正理想点与预期值作为双参照,充分考虑决策问题的外部竞争优势以及内部自身特点,使得决策更加全面,以满足决策专家的实际需要。为此,拟将考虑双参照点的累积前景理论与区间二型模糊数相结合,定义区间二型模糊前景效应、区间二型模糊前景价值函数以及区间二型模糊累积前景价值。在此基础上,提出累积前景Shapley区间二型模糊Choquet积分(CPSIT2FC)算子,以充分反映决策专家的行为偏好。
鉴于以上分析,结合实际决策需求,本文提出一种考虑专家行为偏好与准则关联的区间二型模糊多准则决策方法。为从外部竞争优势与内部自身特点两方面考虑风险型多准则决策问题,本文运用区间二型模糊前景效应以及区间二型模糊价值函数,分别计算针对正理想点与预期值的价值函数;引入预期侧重系数,计算各个方案准则在各状态下的综合价值;依据区间二型模糊累积前景价值,计算各个准则下的累积前景值;建立基于区间二型模糊双向投影以及Shapley函数的权重优化模型,计算准则集的模糊测度,客观确定准则集的权重;利用CPSIT2FC算子,充分考虑准则间的复杂关系以及决策者的行为偏好,计算各个方案的综合累积前景值,据此实现方案的排序和选优。
1 预备知识
1.1 区间二型模糊数
定义1[3]设X为论域,则定义在论域X上的二型模糊集A可以表示为:
A={(x,u),uA(x,u)|∀x∈X,u∈Jx⊆[0,1],
0≤uA(x,u)≤1}
(1)
其中,x是主要变量,Jx⊆[0,1]是x的主隶属度函数,u是次要变量。式(1)可以等价改写成如下形式:

(2)
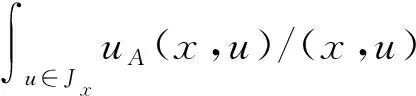
定义2[3]设X为论域,对定义在论域X上的二型模糊集A如果满足uA(x,u)=1,则称A为区间二型模糊集,其数学表达形式如下:
(3)
其中,x表示主要变量,Jx⊆[0,1]表示x的主隶属度函数。
定义3[3]若区间二型模糊数的上下界隶属度函数均为梯形模糊数,则称其为梯形区间二型模糊数,即:
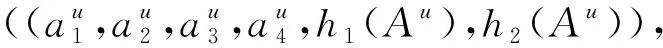
(4)
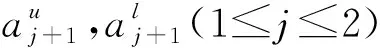
1.2 区间二型模糊数的运算法则
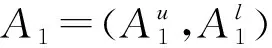
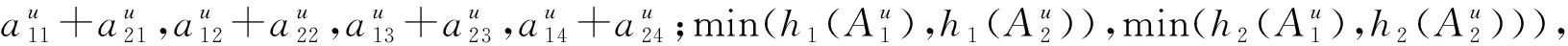
(5)
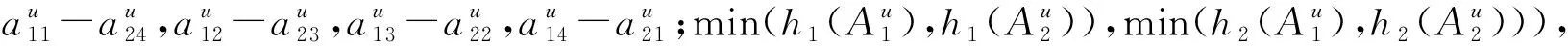
(6)
(7)
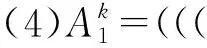
(8)
由定义4可知,数乘运算仅定义了梯形区间二型模糊数与任意非负常数乘积的情形。为满足各类多准则决策方法的应用需求,将其拓展至梯形区间二型模糊数与任意常数的乘积运算,如定义5所述。
定义5设A=(Au,Al)是梯形区间二型模糊数,则A的数乘运算法则为:
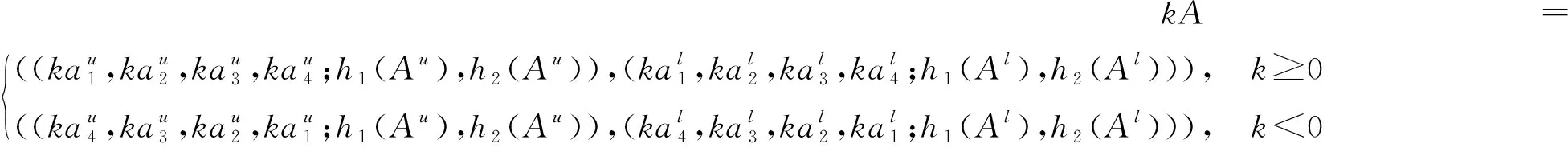
(9)
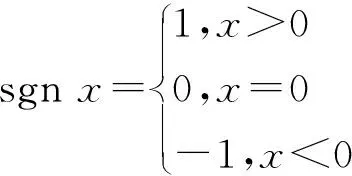
(10)
其中,x∈R。则幂乘运算的具体运算公式见定义6。
定义6设A=(Au,Al)是梯形区间二型模糊数,则A的幂乘运算法则为:

(11)

1.3 区间二型模糊数大小的比较

(12)
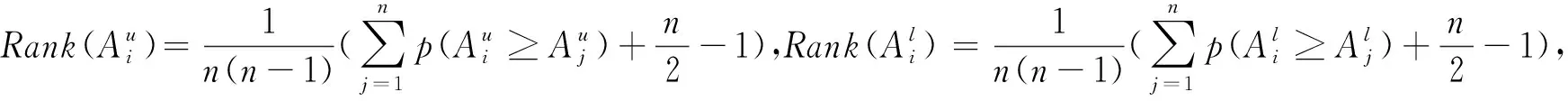
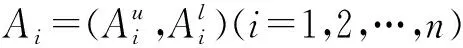
1.4 区间二型模糊数的双向投影
定义9设A=(Au,Al)是梯形区间二型模糊数,则A的模|A|为:
(13)
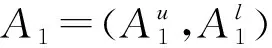
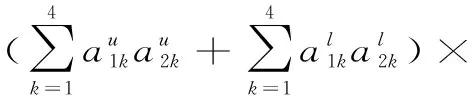
(14)
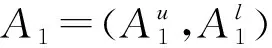
(15)
其中,|A1|是A1的模,|A2|是A2的模,A1·A2是区间二型模糊数A1与A2的内积。
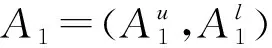
(16)
其中,|A2|是A2的模,A1·A2是区间二型模糊数A1与A2的内积。
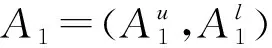
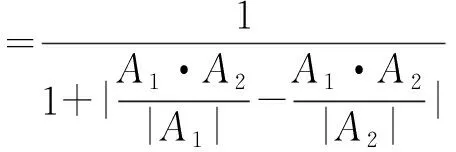
(17)
其中,|A1|是A1的模,|A2|是A2的模,A1·A2是区间二型模糊数A1与A2的内积。
区间二型模糊双向投影测度不仅考虑了A1与A2之间的距离以及夹角,而且考虑了与之间的双向投影的大小。显然,BPj(A1,A2)的值反映了A1与A2的接近程度,其值越大,则A1与A2越靠近;其值越小,则A1与A2越分离。
2 基于Choquet积分的区间二型模糊集成算子及性质
2.1 模糊测度与Choquet积分
定义14[18]设P(X)是X={x1,x2,…,xn}的幂集,μ是定义在X上的集函数μ:P(X)→[0,1],则称μ是定义在X上的模糊测度,若μ满足如下条件:
1)μ(φ)=0,μ(X)=1;
2)μ(B)≤μ(C),∀B,C∈P(X)并且B⊂C。
模糊测度不仅可以表示各个准则以及准则集的权重,还可以表示它们之间的关联关系。
广义Shapley值作为处理具有相互关联准则事物的工具,能够综合考虑准则集的重要程度。
定义15[31]设P(X)是X={x1,x2,…,xn}的幂集,μ是定义在X上的模糊测度,则对于∀S∈P(X),其广义Shapley值为:
(18)
其中,S为X的任意一个子集,XS为X和S的差集,T为XS的任意一个子集,n,t与s分别是X,T与S的基数。广义Shapley值不仅反映了单个准则或准则(联盟)之间对整个联盟的一种贡献值,而且反映了单个准则或准则(联盟)之间对整个联盟的整体平均贡献。
从式(18)得知,当中只含有一个元素时,式(18)将归约为Shapley函数:
(19)
定义16[32]设f为定义在X上的非负函数,μ为定义在上的模糊测度,则f关于模糊测度μ的Choquet积分定义如下:
(20)
其中,(i)为f(x(i))向量变换,使得0≤f(x(1))≤f(x(2))≤…≤f(x(i)),A(i)=(x(i),x(i+1),…,x(n)),且A(n+1)=φ。
2.2 Shapley区间二型模糊Choquet积分算子
为全面考虑准则间的关联关系,把Choquet积分算子与广义Shapley值拓展到区间二型模糊集,提出Shapley区间二型模糊Choquet积分(SIT2FCI)算子。
定义17设X={x1,x2,…,xn}是有限准则集,Ai(i=1,2,…,n)是定义在X上的一组梯形区间二型模糊数,则SIT2FCI算子公式如下:
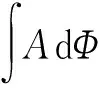
(21)
其中,(i)是Ai的变换,使得A(1)≤A(2)≤…≤A(n),Γ(i)=(x(i),x(i+1),…,x(n)),Γ(i+1)=φ,且Φ(μ(Γ(i)))(i=1,2,…,n+1)是关于模糊测度μ(Γ(i))的广义Shapley值。
定理1设X={x1,x2,…,xn}是有限准则集,Ai(i=1,2,…,n)是定义在X上的一组梯形区间二型模糊数,则由SIT2FCI算子集成得到的结果仍为一梯形区间二型模糊,且有:
SIT2FCI(A1,A2,…,An)
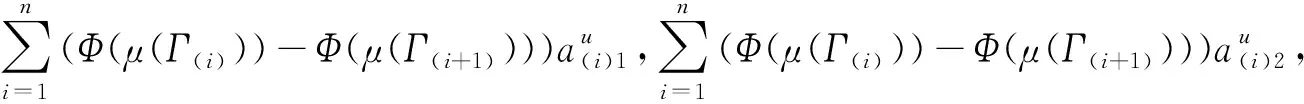
(22)
其中,(i)是Ai的变换,使得A(1)≤A(2)≤…≤A(n),Γ(i)=(x(i),x(i+1),…,x(n)),Γ(n+1)=φ,且Φ(μ(Γ(i)))(i=1,2,…,n+1)是关于模糊测度μ(Γ(i))的广义Shapley值。
2.3 Shapley区间二型模糊Choquet积分算子的性质
设X={x1,x2,…,xn}是有限准则集,Ai(i=1,2,…,n)与Bi(i=1,2,…,n)是定义在X上的两组梯形区间二型模糊数,(i)是Ai与Bi的变换,使得A(1)≤A(2)≤…≤A(n),B(1)≤B(2)≤…≤B(n),Γ(i)=(x(i),x(i+1),…,x(n)),Γ(n+1)=φ,且Φ(μ(Γ(i)))(i=1,2,…,n+1)是关于模糊测度μ(Γ(i))的广义Shapley值,则SIT2FCI算子具有如下性质。
性质1(置换不变性) 若(B1,B2,…,BN)是(A1,A2,…,An)的任一置换,则可以得到如下等式:SIT2FCI(A1,A2,…,An)=SIT2FCI(B1,B2,…,Bn)。
性质2(幂等性) 若Ai=A(i=1,2,…,n),则有:SIT2FCI(A1,A2,…,An)=SIT2FCI(A,A,…,A)=A。
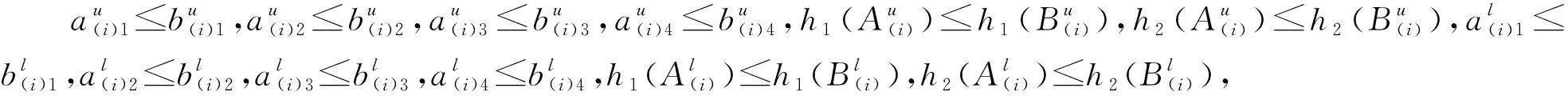
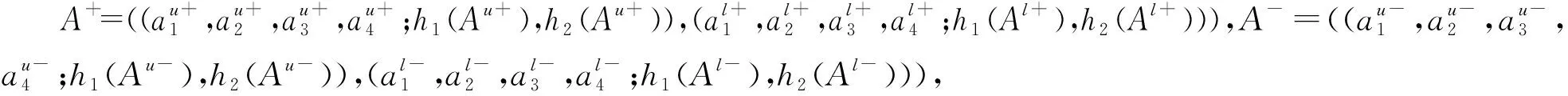
3 基于累积前景理论与Choquet积分的区间二型模糊集成算子
SIT2FCI算子虽然可以全面考虑属性之间的关联关系,但是无法反映决策专家的行为特征信息。累积前景理论[25]是关于风险偏好的决策描述性模型,能够很好地反映决策专家的心理行为。因此,将累积前景理论拓展到SIT2FCI算子,提出累积前景SIT2FCI(CPSIT2FCI)算子,以增强信息集结的合理性与有效性,使决策结果更加符合实际情形。
3.1 累积前景理论
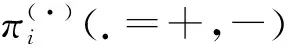
V(f)=V(f+)+V(f-)
(23)
价值函数v(Δxi)能够反映决策专家的风险态度和主观偏好,其具体形式如下:
(24)
其中,Δxi表示xi偏离参照点x0的程度,若Δxi≥0,则表示收益,否则为损失;α,β是风险态度系数,0<α,β≤1,α,β越大表示决策专家越趋向冒险;θ是损失规避系数,通常取θ>1,表明决策专家对损失更加敏感。
(25)
(26)
当存在两个及以上风险前景时,Prelece[33]给出的w+(.)和w-(.)分别为:
(27)
(28)
其中,w+与w-分别表示面临收益与损失时的决策函数,γ+、γ-与φ表示决策权重函数中的主观系数,不同的取值表示决策专家对于事件发生概率非完全理性的程度。学术界对主观系数的取值研究很多,Goda与Hong[34]建议γ+=γ-=0.8,φ=1。
3.2 累积前景Shapley区间二型模糊Choquet积分算子
定义18设Ai(i=1,2,…,n)是一组梯形区间二型模糊,基于累积前景理论的准则参考点假定为A0,则关于Ai的区间二型模糊前景效应为:
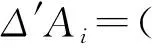
(29)
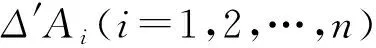
(30)
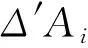
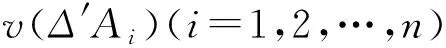

定义21设X={x1,x2,…,xn}是有限准则集,ΔAi(i=1,2,…,n)是一组定义在X上的关于Ai区间二型模糊累积前景价值,则CPSIT2FCI算子公式如下:
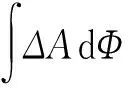
(31)
其中:(i)是ΔAi的变换,使得ΔA(1)≤ΔA(2)≤…≤ΔA(n),Γ(i)=(x(i),x(i+1),…,x(n)),Γ(n+1)=φ,且Φ(μ(Γ(i)))(i=1,2,…,n+1)是关于模糊测度μ(Γ(i))的广义Shapley值。
4 基于区间二型模糊数的多准则决策方法
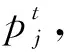
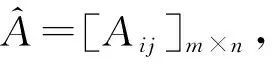
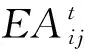
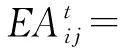
(32)
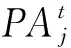
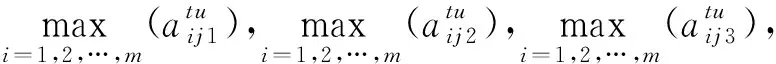
(33)
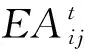
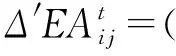
(34)
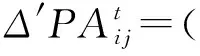
(35)
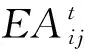
(36)
(37)
其中,本案例中取α=β=0.88,θ=2.25,由于Kahneman和Tversky[25]发现参数α=β=0.88,φ=2.25时与经验数据较为一致。

(38)
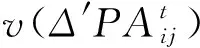
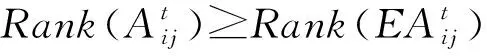
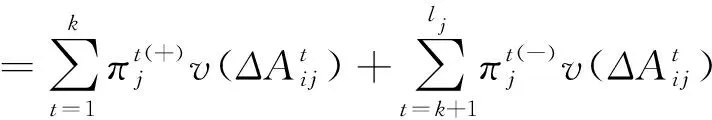
(39)
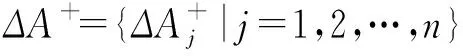
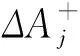
(40)

(41)
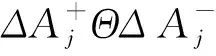
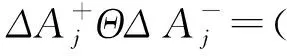
(42)
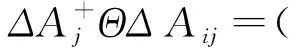
(43)
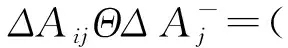
(44)
最后,当准则权重部分未知时,构造如下模型,求解准则集的模糊测度。
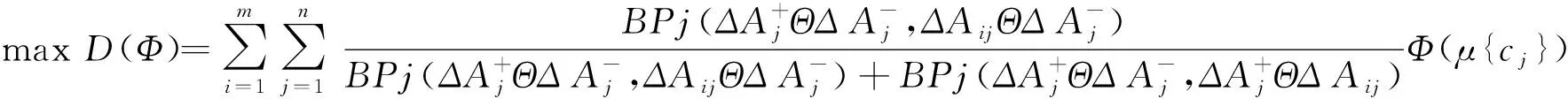
(45)
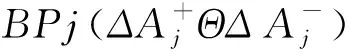
步骤8根据式(18),确定准则集的广义Shapley值,即:
(46)
其中,S为C的任意一个子集,CS为C和S的差集,T为CS的任意一个子集,n,t与s分别为C,T与S的基数。
步骤9利用式(31)所示的CPSIT2FCI算子对决策矩阵[ΔAij]m×n中第i行的各个准则下的累积前景值进行集成,从而得到每一方案的综合累积前景值ΔAi,即:
ΔAi=CPSIT2FCI(ΔAi(1),ΔAi(2),…,ΔAi(n))
(47)
其中,(j)是ΔAij的变换,使得ΔAi(1)≤ΔAi(2)≤…≤ΔAi(n),Γ(j)=(c(j),c(j+1),…,c(n)),Γ(n+1)=φ,且Φ(μ(Γ(j)))(j=1,2,…,n+1)是关于模糊测度μ(Γ(j))的广义Shapley值。
步骤10根据定义7,计算方案zi(i=1,2,…,m)的综合累积前景值ΔAi的排序值Rank(ΔAi)。
步骤11根据定义8,对评价方案Z=(z1,z2,…,zm)的优劣进行排序,并选择最优方案。
5 实例分析
某投资者拟从4支候选股票Z=(z1,z2,…,zm)中选取一支进行投资决策。为了判断股票的盈利能力,专家根据4个准则C={c1:每股收益,c2:每股净值,c3:市盈率,c4:利润增长率}来对各股票进行评估。由于外界环境不确定的影响,每个准则对应3种自然状态Θ={θ1:好,θ2:中等,θ3:差},其发生的概率经专家评估分别为0.1,0.6,0.3。四个准则的权重向量为0.25≤μ({c1})≤0.45,0.3≤μ({c2})≤0.4,0.2≤μ({c3})≤0.4,0.1≤μ({c4})≤0.3。专家利用表1所示的梯形区间二型模糊数来评价4支股票,给出的语言决策矩阵如表2所示,试确定4支股票的排序。

表1 语言标度及其对应的梯形区间二型模糊数

表2 语言决策矩阵
基于梯形区间二型模糊数的多准则决策的主要步骤如下:
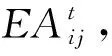

表3 多准则决策预期矩阵
其次,计算各个准则下的累积前景值ΔAij(i=j=1,2,3,4),结果见表4。
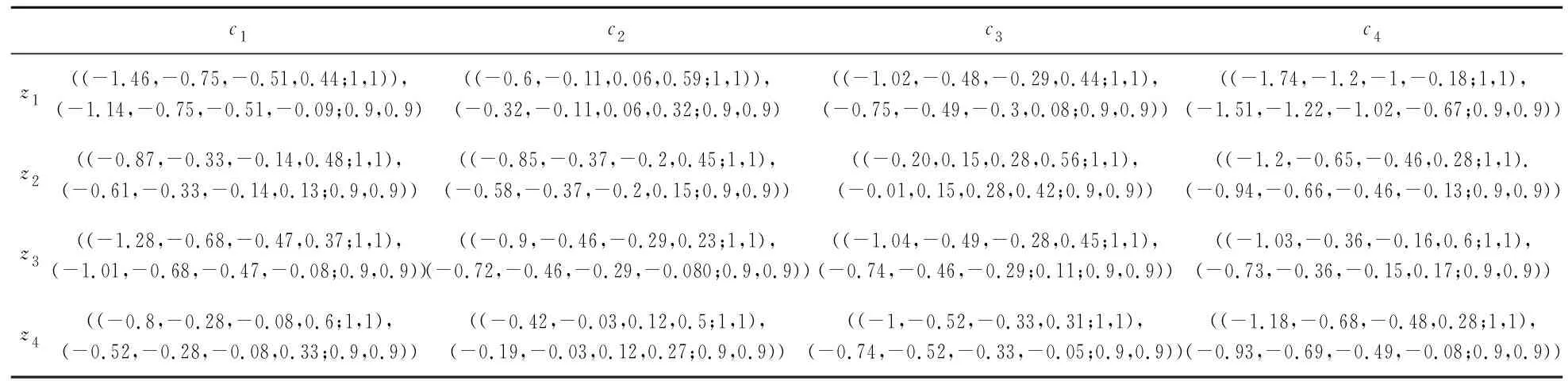
表4 各方案准则状态下的累积前景价值
然后,建立如下权重优化模型,求解准则集的模糊测度,即:
maxD(Φ)=-0.0313(μ({c1})-μ({c2,c3,c4}))+0.0047(μ({c2})-(μ({c1,c3,c4}))+0.0102(μ({c3})
-(μ({c1,c2,c4}))+0.0164(μ({c4})-(μ({c1,c2,c3}))-0.0133(μ({c1,c2})-(μ({c3,c4}))
-0.0106(μ({c1,c3})-(μ({c2,c4}))-0.0075(μ({c1,c4})-(μ({c2,c3}))+1.9119
所得结果为:μ({c1})=0.25,μ({c2})=μ({c3})=μ({c4})=μ({c1,c2})=μ({c1,c3})=μ({c1,c4})=μ({c2,c3})=0.3,μ({c2,c4})=μ({c1,c2,c3})=μ({c1,c2,c4})=0.3,μ({c3,c4})=μ({c1,c3,c4})=μ({c2,c3,c4})=1。
最后,计算方案zi(i=1,2,3,4)的综合累积前景值ΔAi的排序值Rank(ΔAi),即:Rank(ΔA1)=0.1730,Rank(ΔA2)=0.3133,Rank(ΔA3)=0.2725,Rank(ΔA4)=0.2412。因此,评价方案Z={z1,z2,z3,z4}的排序为z2≻z3≻z4≻z1。
为了验证本文提出的方法的可行性与有效性,分别利用不同的侧重预期系数、Qin等[10]的方法以及Gong等[15]的方法对以上实例进行排序,结果如表5所示。

表5 方案排序结果
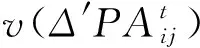
与Qin等[10]的方法以及Gong等[15]的方法相比,本文所提出的方法主要有以下优势:
1)本文的方法以及Gong等[15]的方法基于梯形区间二型模糊数的基本运算法则,集成结果仍是梯形区间二型模糊数,可以有效避免信息损失。而Qin等[10]的方法基于梯形区间二型模糊数的距离,把梯形区间二型模糊数转化成实数,存在一定的信息损失。
2)本文的方法基于Shapley区间二型模糊Choquet积分算子,能够考虑准则之间的冗余、互补以及独立关系。该算子基于如下不等式:μ({c1})+μ({c2})=0.55>μ({c1,c2})=0.3,μ({c3})+μ({c4})=0.6<μ({c3,c4})=1,故本文的方法能够考虑准则c1与c2之间的负相互作用,准则c3与c4之间的正相互作用。Gong等[15]的方法利用几何Bonferrion平均算子,能够通过集成参数考虑准则之间的同质关系,无法通过权重反映准则之间的异质关系。而Qin等[10]的方法利用VIKOR方法,基于准则之间相互独立的假设,无法考虑准则之间的关联关系。
3)本文的方法基于考虑双参照点的累积前景理论,Qin等[10]的方法是基于以其他方案为参照点的前景理论,而Gong等[15]的方法基于期望效用理论,无法考虑决策者心理行为。与前景模型相比,累积前景模型能够较好解决随机强势占优及多个结果的处理问题。本文同时设置正理想点与对方案的预期值作为双参照点,能够体现方案综合指标值的绝对优势以及反映决策者对不同特点的方案具有不同的主观要求。
4)本文的方法利用基于区间二型模糊双向投影以及Shapley函数的权重优化模型来求解准则集的模糊测度,可以客观确定准则集的权重,而Qin等[10]的方法以及Gong等[15]的方法基于权重信息已知的假设,无法直接用于解决准则权重信息部分未知的多准则决策问题。
6 结论
针对准则值为区间二型模糊数,准则之间存在关联关系,决策专家为有限理性,准则权重信息部分未知的风险型多准则决策问题,本文提出了一种多准则决策方法。本文的主要贡献在于:1)补充完善梯形区间二型模糊数的数乘与幂乘运算法则,以满足各类多准则决策方法的应用需求;2)提出区间二型模糊数的投影以及双向投影,以度量区间二型模糊数之间的接近程度;3)提出Shapley区间二型模糊Choquet积分算子,以全面考虑准则之间的关联关系;4)定义区间二型模糊的前景效应、前景价值函数、累积前景价值以及提出了累积前景Shapley区间二型模糊Choquet积分算子,以反映决策专家的主观心理行为;5)建立基于区间二型模糊双向投影与Shapley函数的权重优化模型,以客观确定准则集的权重;6)给出一种基于区间二型模糊数的多准则决策方法,该方法可以全面考虑准则之间的冗余、互补以及独立关系,反映专家行为偏好,并且较好地客服了准则集模糊测度人为给定的主观性影响,更加符合现实决策,为解决基于区间二型模糊数的多准则决策问题提供了一条有效途径。

