专利政策视角下的序贯创新决策分析

方文丽，方世建

(中国科学技术大学 管理学院，安徽 合肥 230026)

0 序贯创新中holdup问题

随着现代科学技术的发展，技术创新越来越倾向于“站在前人的肩膀上”，即只有充分利用前人的创新成果才能有效地进行下一步的技术创新。这也就是人们所提到的“序贯创新”。

专利政策保障了创新者的积极性，但是在序贯创新过程中，也可能会延缓技术创新的步伐。Shapiro[1]指出，专利保护可能会导致专利丛林(patent thicket)从而阻碍技术进步。Llobet[2]考虑了专利权的诉讼问题，认为过严的专利保护制度甚至对于专利所有者而言也是有害的。

因为专利政策的存在，前期创新者持有的专利具有法律规定上的“专有性”，这意味着他对后续创新者具有潜在的合法的索取权。后续创新者基于这种专有性技术进行下一步的技术创新的时候，需要进行“专用性”投资。交易费用经济学认为人是有限理性的，具有机会主义特性，交易过程中，交易的一方会利用对方的“专用性”投资采取机会主义行为“钳制”对方，获取可占用性准租。如果专利法对现有专利保护过分，当理性的后续创新者预期到自己的“专用性”投资事后会被专利持有人的机会主义行为“钳制”，专利持有人可以行使合法的索取权剥夺自己后续创新的收益，他就会减少自己的“专用性”投资或者不进行“专用性”投资，结果导致后续创新不足，社会创新资源就不能得到充分利用或者被搁置浪费。

Heller和Esienberg[3]在1998年Science上发表的那篇著名的文章中提出过“反公共地悲剧”的概念。在“公共地悲剧”中，公共资源的过分利用会降低社会福利，而“反公共地悲剧”中，由于交易成本的存在，私有资源则有可能会出现资源利用不足的情况，这也会降低社会福利。没有专利制度，技术创新的成果是“公共资源”，有了专利制度之后，就变成了“私有资源”。所以专利制度避免了“公共地悲剧”，但却有可能陷入“反公共地悲剧”。

Green和Scotchmer[4]提出一个模型认为在信息对称的情况下，前期创新者向后续创新者提供事前的有偿许可可以避免“钳制”问题。Bessen[5]提出在成本信息不对称的情况下，事前许可在实际中应用并不广泛，“钳制”问题不能消除。事实上，如果采取事前报价，若专利持有人愿意以低于事后惩罚的价格转让其技术，则可避免“钳制”的发生。在信息对称的情况下，可以达成互惠交易，避免“钳制”。但是在信息不对称的时候，互惠的交易不一定能达成，不能完全避免“钳制”问题。

本文对成本信息不对称和收益信息不对称两种情况下的序贯创新的决策问题[6]进行了分析，给出了“钳制”发生的条件和概率。

在序贯创新中，最优的专利政策不仅要考虑对于前期创新者的激励，还要考虑对于后期创新者的激励[7,8]。专利制度一方面要足够保护技术创新者的积极性，另一方面也不能过于保护现有专利持有者，因为这会带来对技术创新的“钳制”[9]。为此本文考虑了整个序贯创新过程中的社会福利，对最优的专利政策进行了分析。

1 基本决策模型

考虑序贯创新者的最简单的情况——两期创新模型。由于多期的序贯创新过程可以看作是许多两期创新连接而成，所以并不失其一般性。

假设有两个创新者A和B：

第一期， 创新者A进行技术创新，投入成本cA，实现收益vA，并申请技术专利。别人很容易通过对A的产品的分析得到其技术，但是专利政策保护了A的专有权。

第二期， 后续创新者B如果利用A的技术进一步创新，投入cB可以实现收益vB。B可以有两种选择：一是事前购买A的许可(A的报价为r)；二是在事后依照专利政策规定将自己收益按一定分成s支付svB给A，其中s代表了所有关于专利政策的信息。

为了讨论问题的方便，我们把专利保护政策简化为一个事后的分成比例。这自然是一个外生常量。

在上述假设下，整个技术创新的过程如图1所示：

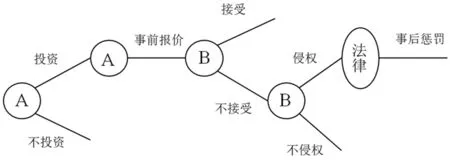
图1 技术创新过程图

在信息对称的情况下，即双方的成本收益都是公共信息。如果没有事前报价，即B必须支付事后的专利使用费(也就是惩罚费)，当vB-cB-svB<0时，B的净利润小于零，不会进行技术创新，也即出现事前投资不足的“钳制”现象。但是如果有了事前报价，作为理性人，A会报价小于事后的惩罚，事实上，信息对称下，A会报价略小于vB-cB，这样B的净利润还是大于零的，所以还是会进行技术创新，即，没有出现“钳制”现象。

但是在信息不对称的情况下，A无法准确地知道vB-cB，这时A只能按照自己的估计进行报价，这个报价就不一定能被B接受，这时就有可能出现“钳制”现象。

2 成本信息不对称下的分析

2.1 最优决策和“钳制”问题

假设vB是A和B都知道的公共信息。cB是B的私人信息，A只知道cB服从F(.)的分布，显然F(0)=0，F(vB)=1。

(1)如果vB-cB-svB<0，那么如果采用事后分成的方法，B的净利润为负，所以只有事前购买可能发生。

A提出r报价时，他的第二期期望收益X1(r)等于r乘以B接受其报价的概率，后者也就是使得B的净利润为正的概率，即:

X1(r)=rPr{vB-cB-r>0}=rF(vB-r)

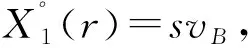
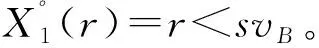
所以按照理性人假设，A会选择事后分成。

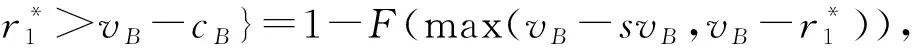
(a)如果vB-cB-svB<0，就有可能会产生A对于B技术创新的“钳制”；如果vB-cB-svB≥0，不会发生“钳制”。

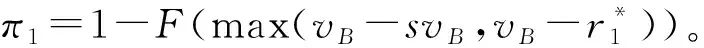
2.2 最优专利政策

最优的专利政策应该使得社会福利最大，所以本节中将讨论整个技术创新过程的社会福利，然后求出最优专利政策，也就是求最优的s。

假设对于专利政策制定者而言，vA和vB是已知确定的信息，而cA和cB是不确定信息，分别服从分布F(.)和G(.)。易知，在确定A和B都进行技术创新的情况下，总的社会福利应该等于vA+vB-cA-cB；在不确定的情况下，考虑各创新发生的概率然后分别按照vA-cA和vB-cB积分即可。

当vB-cB-svB<0时，有社会福利W11满足：

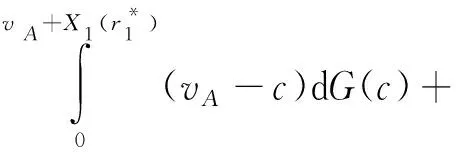
(1)

当vB-cB-svB≥0时，同理可以得到社会福利W12满足：

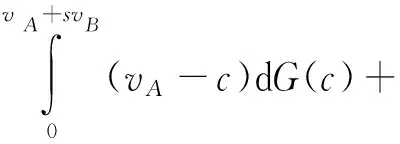
(2)

所以期望社会福利W满足:

W1(s)=W11Pr{vB-cB-svB<0}+W12Pr{vB-cB-svB≥0}

=W11[1-F(vB-svB)]+W12F(vB-svB)

(3)

其中W11和W12分别由Eq.(1)和Eq.(2)给出。

(4)

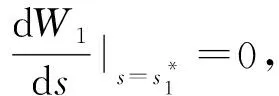
3 收益信息不对称下的分析

3.1 最优决策和“钳制”问题

假设vB是B的私人信息，A只知道vB服从H(.)的分布。cB是A和B都知道的公共信息。

(1)如果vB-cB-svB<0，那么如果采用事后分成的方法，B的净利润为负，所以只有事前购买可能发生。如前面相似，同理可以得到A在二期创新中的期望收益X2(r)满足：

X2(r)=rPr{vB-cB-r>0}=r[1-H(r+cB)]

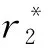
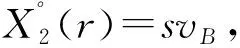
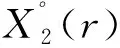
(2)中，B一定会进行后期的创新，所以A对其技术的专有性没有对B技术创新产生“钳制”。综合上述两种情况，可以得到出现“钳制”的概率为:

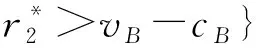
所以在序贯创新的成本信息不对称的情况下：

(a)如果vB-cB-svB<0，就有可能会产生A对于B技术创新的“钳制”；如果vB-cB-svB≥0，不会发生“钳制”。

3.2 最优专利政策

同样，通过讨论整个技术创新过程的社会福利可得出最优专利政策。

假设对于专利政策制定者而言，cA和cB是已知确定的信息，而vA和vB是不确定信息，分别服从分布M(.)和H(.)。

同2.1节相似，在不确定的情况下，考虑各创新发生的概率，然后分别按照vA-cA和vB-cB积分即可得到社会福利。

当vB-cB-svB<0时，社会福利W21满足:

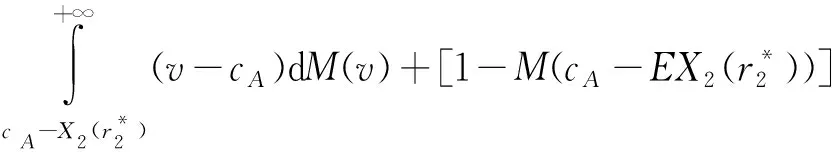
(5)

当vB-cB-svB≥0时，同理可得社会福利W22满足:

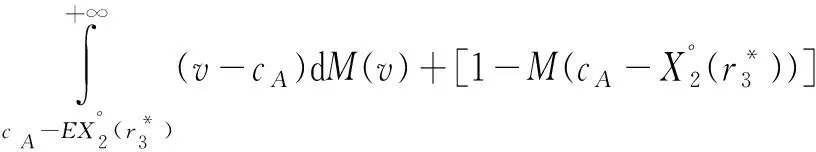
(6)

所以期望社会福利W满足:

W2(s)=W21Pr{vB-cB-svB<0}+W22Pr{vB-cB-svB≥0}

(7)

其中W21和W22分别由Eq.(5)和Eq.(6)给出。

(8)

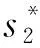
4 钳制问题的解决

4.1 多次报价下的扩展

在多次报价下，如果不考虑谈判成本，信息不对称的状况会被消除。在本模型中，如果还是只有A和B两个创新主体的情况下，作为前期创新者，A只要能够卖出技术专利，就可以给他带来额外的受益，而又只能卖给B，所以在技术转让谈判中，A会不断降价，即他的成本底线为零。所以B在知道这种情况之后，会不断地拒绝A的报价，直到A报价近似为零。这实质上也就是完全避免了A对B“钳制”问题的产生[10]。但也产生了B对A的“钳制”，因为A只能卖给B，所以A所拥有的技术也具有了“专用性”，也有可能被B所钳制。

4.2 多个后期创新者下的扩展

当市场上存在多个后期创新者时，下面考虑前期创新者A只能将其技术许可给一个主体使用，且后期创新者之间产生竞争的情况。不失一般性，考虑两个后期创新者B1，B2，且B1(B2)使用A的技术进行创新的成本为cB1(cB2)，收益为vB1(vB2)。A的转让过程可以通过拍卖等方式进行，在这里不考虑具体的报价过程，只考虑B1或B2所能愿意付出的最大报价。为此就必须考虑B1或B2得到其技术使用权之后的收益情况。

假设B1支付给A以P1的费用得到其技术的专有使用权。这个使用专有权使得B2如果对A的技术进行侵权就要受到法律的惩罚。由于B1和B2之间存在竞争，所以如果B1进行创新而B2不创新，那么B1将从B2那里争取到市场份额从而获得收益M(M>0)，这时B2损失M，反之同理。但是如果B1和B2都进行创新，那么双方的市场份额不变。B2因为“侵权”而应该支付给B1的赔偿，我们也按照M来定义。同前面一致，我们用s(s>0)来代表法律规定的赔偿系数。

双方各有两种选择，所以可得其博弈矩阵[11]如表1所示。

表1 博弈矩阵

易知，当vB1-cB1>(s/2-1)M且vB2-cB2>(s-1)M时，该博弈存在纳什均衡解(创新，侵权)。

这时，B1的净收益为-P1+sM/2+vB1-cB1。所以可得当初与A进行谈判的时候，B1所能的接受最高报价为sM/2+vB1-cB1。对比前面只有一个后期创新者的情况，报价的范围提高了sM/2。从前面可以得知出现的“钳制”问题的条件是A的报价超过B所能接受的条件。所以可接受报价范围提高自然使得出现“钳制”问题的概率就变小了。

综上可知扩展到多个后期创新者，“钳制”问题有可能部分得到解决。这是因为前面假设前期创新者在转让其技术的同时也转让了其技术“专有”权，所以使得获得者可以“钳制”其他后期创新者，从而部分避免了自己被“钳制”的状况。相反，可以看到如果前期创新者没有出让其技术“专有”权，即其技术可以同时转让给多个后期创新者，那么“钳制”不但没有得到避免，反而还会加深，因为后期创新者的利润进一步降低了，其可接受报价的范围也就减少了。

5 结束语

随着科技的发展，序贯创新已经逐渐成为现阶段创新的主要形式。专利政策使得前期创新者获得了其技术的“专有性”，这使得后期创新者的投资变成“专用性”投资，这就有可能出现“钳制(holdup)”问题。我们的分析表明信息不对称下，这个问题无法得到完全解决。专利政策要在保护前期创新者的利益和激励后期创新者进行创新间进行权衡[12]。最优的专利政策应使得社会福利最大化，本文给出了最优专利政策满足的条件。

在我国经济现实中，由于以前对于知识产权的忽视，现在“矫枉过正”，人们往往较多地关注于对前期创新者的保护，以致对现有专利过于保护，事实上“物极必反”，对现有专利的过于保护对于可持续的技术创新也是有害的。现实的复杂性常常使我们无法实施理论上最优的专利政策，权衡中获得的满意应该是个理想的结果。