双模式网络停车限制交通需求管理模型与方法研究
刘炳全,度 巍
(1.渭南师范学院 数学与统计学院,陕西 渭南 714099; 2.南通大学 交通与土木工程学院,江苏 南通 226019)
0 引言
随着中国大中城市汽车保有量的持续增加,以私人小汽车为主的道路网交通模式给有限的道路资源带来巨大压力,急剧增长的私家汽车出行需求带来交通拥堵、环境污染等诸多问题。研究如何采用有效方式减轻交通拥堵、使出行需求得到合理规划和管理吸引了交通部门及管理学者的重视,其中通过收费方式来抑制私家车的出行需求成为近十年来交通理论界研究的重要课题。理论上,拥挤收费是城市交通需求和拥挤管理的有效方式[1,2],通过对个别路段征收道路通行费,使出行路线费用增加,可迫使部分出行者改变出行路线或模式甚至放弃出行计划,以起到改善交通出行的目的。但拥挤收费在实践中由于所收费用的归属与使用一直存在争议,目前除了少数几个地区已经实施外,更多的是理论上的探讨[1]。此外,停车收费也被认为是交通拥挤管理中的一种方法[3~5],将用户到达终点时缴纳的停车管理费作为出行的广义费用,使私人小汽车用户整体出行费用提升,迫使部分用户转变出行方式, 从而可以在一定程度上抑制私家车的出行。秦焕美等[6]采用浮动式停车收费模式研究停车寻泊行为,分析了停车收费价格浮动变化下用户停车选择行为的作用机理,给出了一种定价方案;范文博等[7]研究了不同运营机制停车收费问题,建立了停车收费与用户出行均衡的二层规划模型,并设计灵敏度分析法进行求解。在停车收费和车位分配方面,朱成娟等[8]依据收费利润最大和社会总花费最小原则,建立了一种三层Stackelberg博弈模型研究分配策略和停车收费价格。然而在实际的城市道路网络中,较低的停车管理费有时并不能有效限制交通需求,而提高停车费又容易引起社会公众的不满,因此也有必要对停车限制进行研究。Zhang等[9]在多起点-单终点交通网络研究了有限停车供应问题,提出了一种新颖的可交易停车许可方案;Wang等[10]研究了停车限制系统和收费问题,建立一个二层博弈模型来获得最优收费方案可使社会福利达到最大。仍然,现有文献主要对终点停车供应方面进行研究,即在给定的停车容量下,研究停车位的竞争均衡和车位交易问题,而较少从交通规划和管理方面分析和研究停车限制问题。
在北京、武汉等大型城市,轨道交通模式已受到交通管理部门的高度重视,作为一种高容量且快速准时的大众出行方式,地铁或轻轨等轨道交通逐渐成为城市公共交通的主干。由于轨道交通路网不会与现有公路交通发生冲突,而且几乎连接了整个都市的商业和经济中心,其在制约私家车过度使用,将汽车出行需求引向公共交通出行方面具有重要作用。由于轨道交通与降低公路网交通拥堵、提升交通环境具有密切联系,因此本文研究的路网是指公路网和轨道网混合的双模式交通网络。
现有文献主要在公路交通网络中研究停车问题[11~13],然而轨道网和公路网并存的双模式网络更加符合实际,当合理优化终点的停车需求容量时,可使出行者向轨道网络转移,从而起到了限制汽车出行的目的。因此本文在双模式网络中研究如何对终点停车容量进行设计以管理出行需求问题,建立的模型考虑了路段和停车容量约束以及停车收费问题,更加符合实际。用户的出行模式和路线选择行为通过求解二元Logit模型和随机用户均衡的不动点问题得到,从而该模型是一个带不动点约束的数学规划问题。由于这种模型的求解非常困难,本文设计了一种灵敏度分析法,以获取各路段流量和需求量关于终点容量波动的最终梯度信息。最后通过一个网络例子进行数值实验,验证了相关模型和算法的有效性和合理性,并分析了不同停车收费策略对总系统费用、终点设计容量、终点等车延误、停车需求等的影响。
1 双模式网络Logit随机用户均衡问题
1.1 相关表述
ps,s∈D为单位流量车辆的停车费用,β为时间价值;c=(…,ca,…)T为公路网路段环境容量;
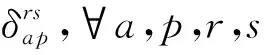
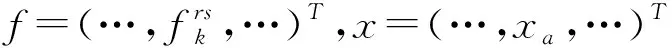

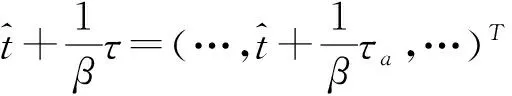

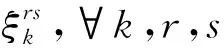
λ=(…,λs,…)T为出行者到达终点的等车延误。
分布参数θ反映公路网用户对各OD对间最短路信息的掌握程度,θ值越高,表明用户对路网信息掌握的越好。对公路交通网络,汽车出行用户不仅具有出行终点停车需求限制,还存在各路段的环境容量约束,则对应的流量守恒和约束为:
(1)
(2)
(3)
(4)
(5)
需要注意的是,环境容量要小于路段实际容量,通常是规划者为保护交通环境设计的虚拟容量,如果没有外部约束,出行者一般不会遵守环境容量。
1.2 双模式网络出行和路线选择均衡
在双模式交通网络中用户可根据自身的出行负效用来选择出行模式,公路网用户的期望行驶负效用为:
(6)
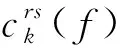
同样地,对轨道网期望出行负效用(广义出行时间)是可以预先确定的常数,有:
(7)
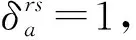
交通需求的模式划分遵循二元Logit原理,即:
(8)
选择参数ξ反映出行者对模式选择的偏爱程度,ξ越大,表明用户越偏爱期望负效用小的出行模式。
根据效用最大化理论,可知公路网的路线选择概率为:
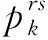
(9)
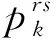
(10)
(11)
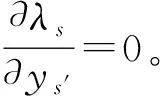
2 双模式网络交通需求管理模型
双模式交通需求拥挤管理模型目标是在(1)~(11)的随机均衡约束下设计最优停车容量使整个网络总出行负效益或总费用成本达到最小,该模型可表示为如下一个具有不动点约束的数学规划问题:
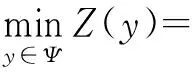
(12)
(16)
其中:Ψ={y|ymin≤ys≤ymax,∀a∈A,s∈D}。
式(12)表示整个网络总出行负效益或总费用成本,第一项为公路网和轨道网所有用户的出行负效用,第二项为轨道网的总票价,第三项为公路网的停车收费,第二项和第三项可看作是整个系统的效益;约束(13)与(14)分别为公路网与轨道网路段流量,其中公路网路段容量受路段环境容量限制,是一个关于路段流量的不动点模型;约束(16)为终点总需求约束,表明同一终点的停车需求不超过停车总容量。该模型是一种带路段环境容量和终点停车需求容量共同约束的交通需求管理模型,对现实交通情形考虑得更加具体全面。
3 双模式交通需求拥挤管理模型的灵敏度分析法
3.1 路段流量与终点需求的灵敏度分析
由于交通需求拥挤管理模型(12)~(16)是一个具有不动点约束的数学规划模型,求解非常困难,通常采用智能搜索算法,如粒子群算法[14],遗传算法[15]等进行求解,但由于此类算法震荡较大,后期收敛速度通常较慢,且无法容易获得路段流或者终点需求量关于决策变量的波动信息,为此本文设计灵敏度分析算法进行求解。
在最优化模型的求解方法中,灵敏度分析法在求解复杂二层规划或具有均衡约束的数学规划问题时具有很好的应用。该方法是分析优化模型中某个参数发生扰动时对优化目标或目标解的变化是否灵敏的一种方法,主要用来研究初始数据产生扰动时最优解的稳定性[16]。通过灵敏度分析获取目标解对扰动参数的梯度信息还可以发现相关参数对模型的影响。因此,灵敏度分析法在运筹学方法和最优方案评价时具有重要作用。
本文通过灵敏度分析法来获得公路网路段流量和需求量(x,q)关于设计容量比y的灵敏性,即获取各路段流量和需求量关于终点容量波动的梯度信息。
由于终点的排队延误和停车费不会对公路网用户的路线选择概率产生影响,因此当终点排队延误λs>0时,仅仅影响用户的出行模式选择。由互补松弛条件可知:
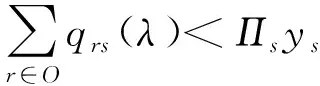
(17)
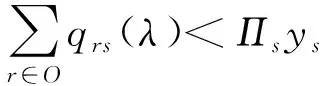
(18)
(19)
从而:
(20)

(21)
进一步有:
(22)
(23)
表明增加停车容量可使轨道路段上的出行量下降。从而合理设计出行终点的停车容量可让汽车与轨道出行需求达到一个均衡模式,使得整个交通系统达到最优状态。
3.2 灵敏度分析法计算步骤
根据上述分析,求解模型(12)~(16)的灵敏度分析算法计算步骤如下:
步骤0(初始化) 给定一个初始期望容量设计比y(0),误差标准ε,置n=0。
步骤1(随机用户均衡问题) 在y(n)下解需求和路段约束Logit随机用户均衡问题,得路段流及需求(x(n),q(n))与乘子λ(n)。
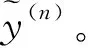
步骤4(一维搜索) 确定步长因子α(n)。

步骤6(收敛标准) 如果‖yn+1-y(n)‖≤ε停止,否则置n=n+1,转步骤1。
注1在步骤1中,y(n)给定后,需要反复求解子问题即需求约束Logit随机用户均衡问题,此时可采用文献[17]中算法进行求解,该算法的收敛速度和结果的准确性是本文灵敏度分析法能够顺利求解的关键。
注2在步骤3中,线性逼近可求解如下子问题:
s.t.ymin≤y≤ymax
其中:

(24)
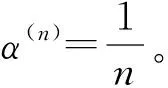
4 数值仿真试验与结果分析

表1 公路网路段初始信息
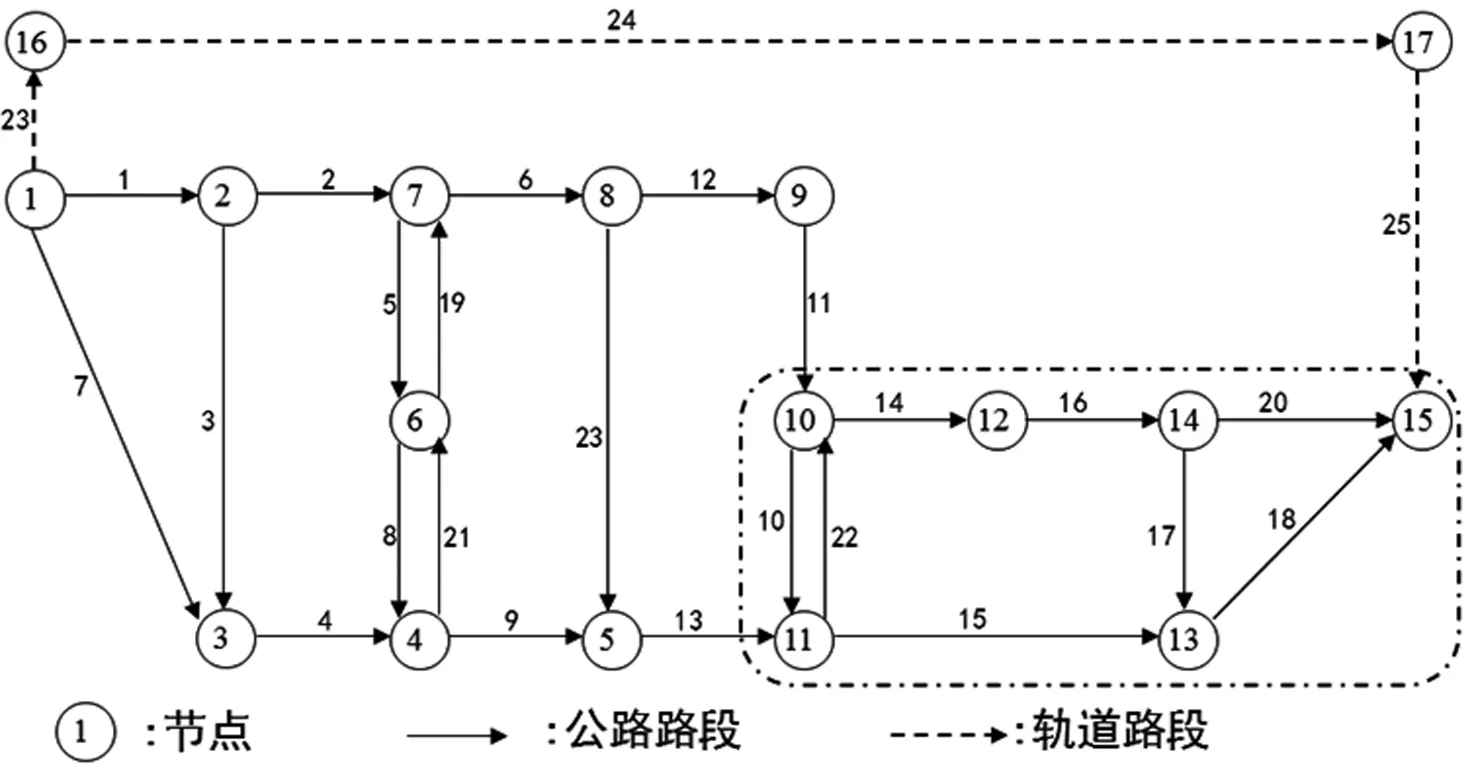
图1 文献[16]双模式交通网络
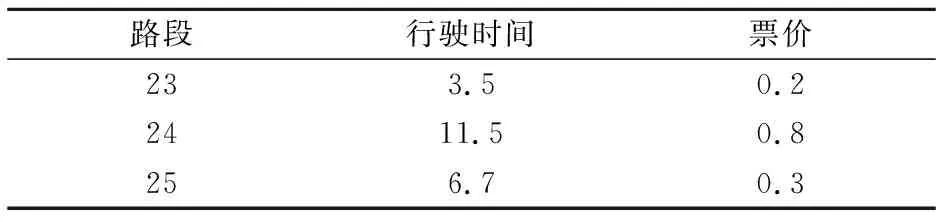
表2 轨道网路段初始信息
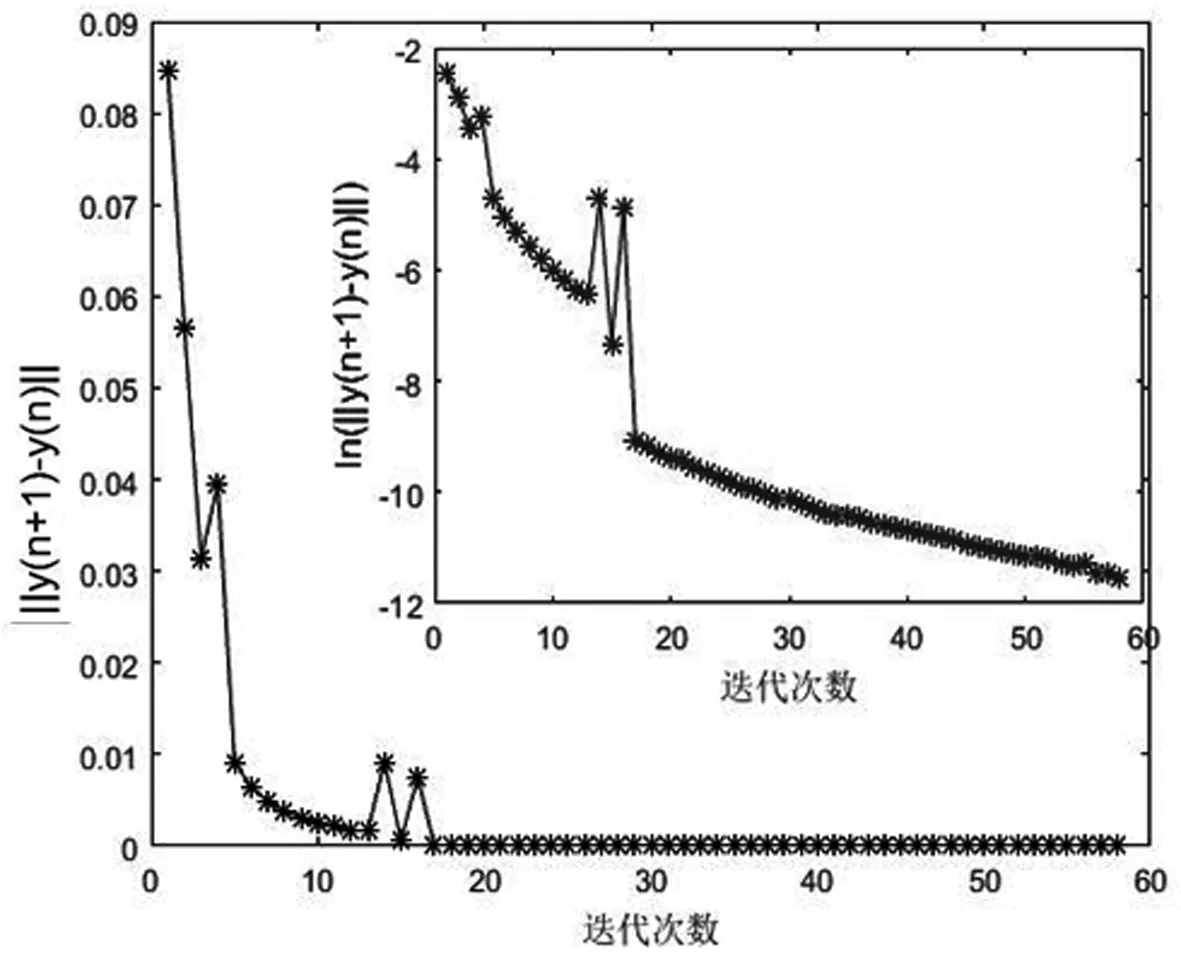
图2 算法收敛曲线
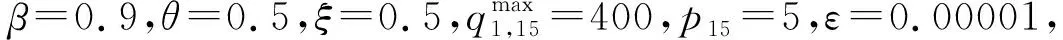
从图2中主图可以发现,算法的收敛速度比较快,17次迭代后就几乎满足收敛标准‖y(n+1)-yn‖≤0.00001,为了更加清晰地观察本算法在17次迭代以后曲线的收敛趋势,将收敛标准两端取对数,即取ln(‖y(n+1)-yn‖)≤ln0.00001,此时通过图2中的子图可以看出收敛曲线在17次迭代以后也具有较明显的下降趋势,表明本算法具有较好的收敛趋势。
图3给出了终点停车收费变化时对停车需求、终点最优设计容量、等车延误以及系统总费用的影响。可以发现,当停车收费价格较低(0≤p15≤8)时,随着停车收费价格的增加,终点等车延误逐步下降,但此时收费变化对终点设计容量和汽车出行需求影响很小,这是因为等车延误的降低抵消了停车费用增加对汽车用户出行的影响,使得公路网汽车出行需求保持稳定;而且随着停车收费价格的增长,停车收益逐步增加,致使系统总费用逐步下降。例如,p15=1时,最优终点停车设计容量和汽车出行需求均为220.2,等车延误λ15=8.3871,系统总出行费用为8.6577×103,而p15=8时,出行需求变化不大,等车延误下降为0,系统总出行费用下降为6.82×103。此时公路网交通出行需求量为220.9,这与停车费用p15=1和5时几乎一致,这表明当出行需求持续保持较高态势时,较低的停车费可引起更高的等车延误,因而并不一定能减少汽车出行费用,而且单靠停车收费并不能很好的管理交通出行需求,这进一步表明优化停车容量具有较高的现实意义。
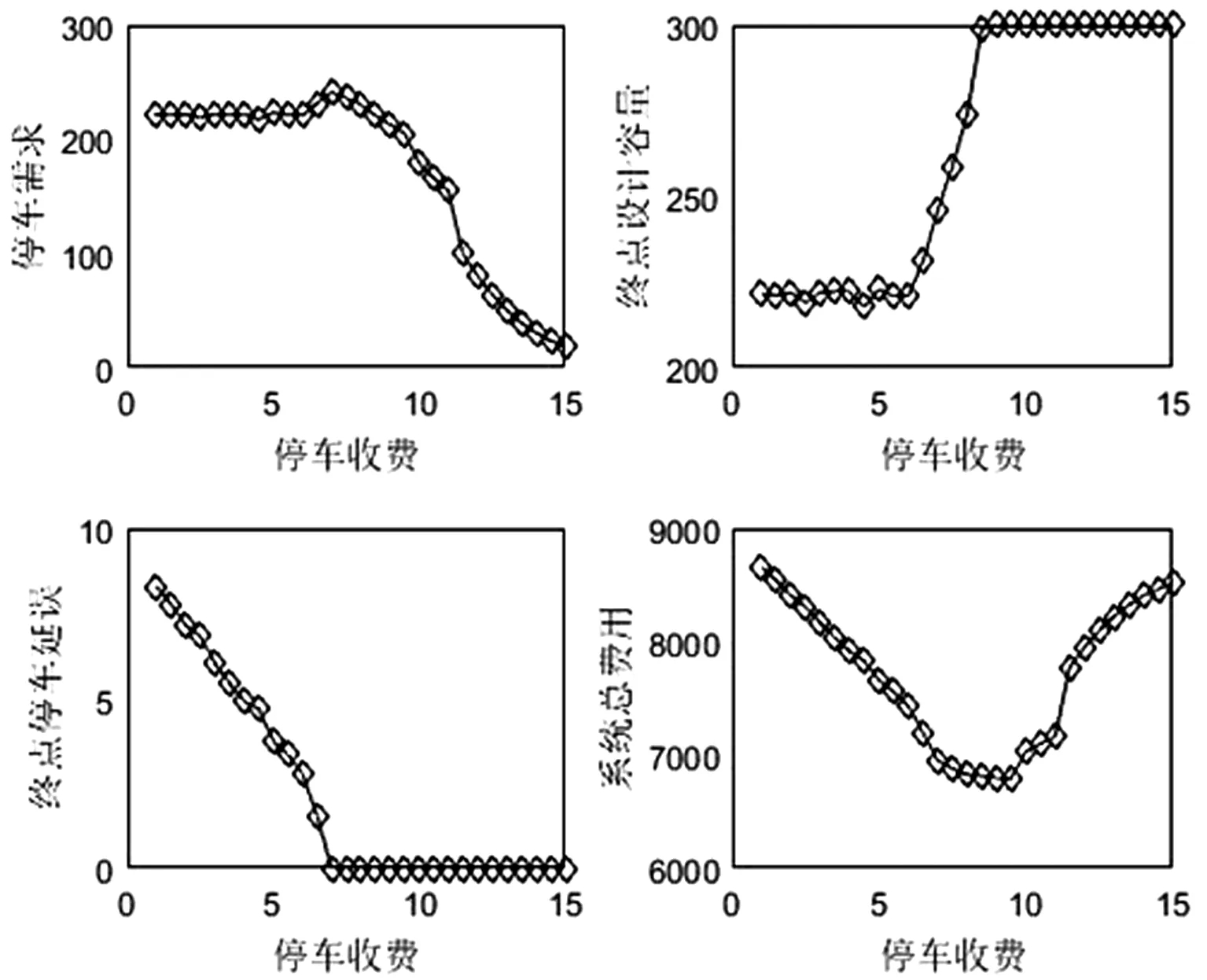
图3 停车收费对各指标的影响
当停车收费价格较高(8 针对公路与轨道混合的双模式交通网络, 本文研究了如何对终点停车容量进行优化设计以达到管理出行需求的目的,建立的一种新的停车限制交通需求管理模型,对实际交通问题考虑的更加合理。由于该模型是一个具有不动点约束的数学规划问题,求解非常困难,为此本文设计一种灵敏度分析算法进行求解。通过数值仿真实验可以发现,灵敏度分析法具有较好的收敛趋势;从仿真结果可以看出,当出行需求比较高时,较低的停车收费并不能很好地管理出行需求,而较高的停车收费也可能导致系统总费用成本的提升,因此同时考虑停车收费与容量优化设计可具有更好的现实意义。在本文中,仅选取了城市轨道交通出行和私家车出行两种交通方式,并没有包含公交车、出租车等公众常见的出行方式,而轨道交通出行用户与公路上选择公交出行的用户往往存在一定的联系。当对汽车出行施行终点停车管控时,势必会造成一部分出行需求转移到道路公交出行上,如何将这部分交通需求的影响考虑进停车限制交通管理模型中,将在后续研究进行分析和探索。5 结论

