考虑应急设施中断风险与防御的可靠性选址模型研究
于冬梅,高雷阜,赵世杰
(1.辽宁工程技术大学 优化与决策研究所,辽宁 阜新 123000; 2.辽宁工程技术大学 运筹与优化研究院,辽宁 阜新 123000)
0 引言
应急设施选址布局决策是支撑并促进应急管理体系发展的关键问题,对应急响应和应急资源的合理分配具有根本影响,是应急服务网络规划建设的核心决策,将在很大程度上影响整个应急服务网络的服务效率和应急响应的能力。应急设施选址-分配优化模型的构建及其拓扑结构的优化方案是灾前预置应急设施选址网络设计的重要内容,决定了应急设施和其提供服务的应急需求点之间的应急资源分配的映射关系。随着突发灾害事件下决策环境的复杂化,选址布局网络面临各种中断风险,决策者在模型构建时需关注多种目标,均衡多重约束,充分考虑中断情境下应急设施的非完全可靠性,确保设施一旦发生中断,应急服务系统和应急服务网络仍能处于良好的运行状态。
考虑设施中断风险的可靠性选址模型由Snyder和Daskin[1]首先提出,相关扩展问题的选址研究多为单目标模型,而考虑中断风险和防御的多目标可靠性优化模型的研究相对较少。文献[2]基于设施的中断风险考虑加固费用建立可靠性P-中位模型和固定费用下无容量限制的选址模型,提出拉格朗日松弛(LR)方法求解模型,给出了资源的结构分配,为设施中断情形下预算决策的制定提供参考。Afify等[3]基于P-中位模型(PMP)和无容量限制设施选址问题(UFL),考虑设施中断对选址布局网络的影响,在加固费用预算下建立抵御中断风险的可靠性选址布局优化模型RPMP和RUFL,设计进化算法求得问题的近似解。Zhang等[4]考虑竞争设施选址问题中设施存在中断的风险,将其建模为Stackelberg博弈问题,将领导者的决策问题建模为双层优化问题,提出了一种变邻域分解搜索算法求解模型,选址优化方案促进了设施网络的可靠性。范厚明等[5]围绕内陆港选址决策问题,考虑了包括多种交通方式的联运网络(涵盖铁路、公路及内河),建立考虑不确定需求和路径失灵概率的内陆港选址布局鲁棒优化决策模型和随机优化决策模型,提出模拟退火-粒子群混合优化算法对模型予以求解和分析,以降低不确定中断因素诱发的风险。Farahani等[6]建立可靠性最大覆盖选址模型,中断情境下以覆盖总需求量最大为优化目标,建立无容量约束的混合整数规划模型,并提出耦合人工蜂群算法求解所构建的模型。Li和Ouyang[7]考虑设施中断的连锁反应,具有相互关联的中断概率,建立固定费用可靠性选址模型,并设计连续化近似求解方法。Rayat等[8]从多目标的角度出发提出了考虑中断因素的选址-分配-库存集成问题,基于部分覆盖设计双目标选址-分配优化模型,同时考虑选址模型中的经济成本和设施中断损失,并根据中断概率确定设施选址方案和优化路径的选择。文献[9]研究最小最大设施选址与加固问题,将设施选址与抵御中断风险的加固决策结合起来,建立以最小化最大服务距离及最小化建立设施数量为目标的多目标选址优化模型,但假设应急设施的服务质量相同,并基于权因子方法将混合整数规划多目标模型转化为单目标模型,采用基于二元搜索的三阶段启发式算法改进解的空间。Garg等[10]针对冗余分配问题考虑系统的中断风险建立多目标可靠优化模型,以系统可靠性和相应的设计成本作为不同的优化目标,提出粒子群算法(PSO)实现对所建立模型的求解,以实例验证模型的有效性。Karatas等[11]考虑了应急设施选址决策的可靠性及分配资源的公平性,融合了经典选址模型中p-中位模型、p-中心模型及最大覆盖模型的优化目标,但假设设施的服务能力是无限的,提出分支定界算法并嵌入迭代全局搜索技术求解模型,获得多目标决策的Pareto边界。更多在选址决策中考虑设施中断风险的文献参见[12~16]。
综上所述,迄今为止的研究表明中断情境对选址-分配方案的优化设计影响显著,已有考虑设施中断风险的设施选址模型大多为单目标优化模型,且大多不考虑设施的容量约束,而已有多目标优化模型鲜有考虑应急设施的服务质量的优化目标、考虑抵御中断风险的加固成本以及考虑加固预算约束集成优化的研究。基于此,综合考虑经济性和服务质量及最大最小容量约束限制,建立考虑中断风险的可靠性应急设施选址分配双目标优化模型。以最小化系统运行成本为目标反映经济性,以最大化期望服务水平反应服务质量,从而在中断环境下合理配置资源,提高应急设施的可靠性和抵御中断风险的能力。
多目标优化问题的解存在冲突的情形,若某个目标达到了求解的要求,但会影响到相关其他目标解的质量,各目标间的设定有时甚至是矛盾的,需对多个目标函数进行折中处理,相互权衡以寻求合适的解决方案,本文利用非支配排序多目标遗传算法(Non-Dominated Sorting Genetic Algorithm Ⅱ, NSGA-Ⅱ)对模型予以求解,获得Pareto非支配解集。
1 问题描述及数学模型
1.1 问题描述
考虑应急设施的中断风险和加固预算构建应急设施可靠性双目标优化模型,从抵御中断风险的视角以系统成本最小化即应急设施的建立成本和抵御设施中断的加固成本为目标反映成本经济性,从应急设施服务质量的视角以最大化覆盖服务质量水平为目标反映服务质量的可靠性,同时均衡考虑加固预算约束和最小最大容量约束,确定应急设施点的位置、需求点在各个应急设施之间的分配及选址-分配网络的拓扑结构。
应急服务质量反映应急设施满足应急需求点的服务能力程度,即应急设施对需求点的服务水平或服务感知度,需求点对应急服务质量需求具有异质性,随着应急设施与需求点之间距离的变化,应急服务质量随之发生变化,基于此,引入应急设施选址布局决策中的应急服务质量覆盖函数,亦称其为服务水平函数或覆盖度,刻画应急需求点感知应急服务质量的满意度(因变量)与服务距离,即应急设施响应应急需求点覆盖距离要求(自变量)的数学关系式。通过应急需求点对覆盖服务质量的满意度与应急设施点和应急需求点之间的距离函数关系,刻画不同应急资源需求点对应急设施提供应急响应的覆盖服务质量的异质性,进而保证选址决策的科学性。
考虑应急需求点对应急服务质量满意度的异质性,本文通过服务质量覆盖函数刻画不同需求点对应急设施提供应急响应的覆盖服务质量的异质性,实现多级服务质量覆盖。设d(i,j)为第i个应急设施与第j个需求点的距离,rs为应急需求点获得应急设施覆盖的最小临界距离,ru为应急需求点获得应急设施覆盖的最大临界距离,rs≤ru,引入如下指数型非线性覆盖函数[17]。
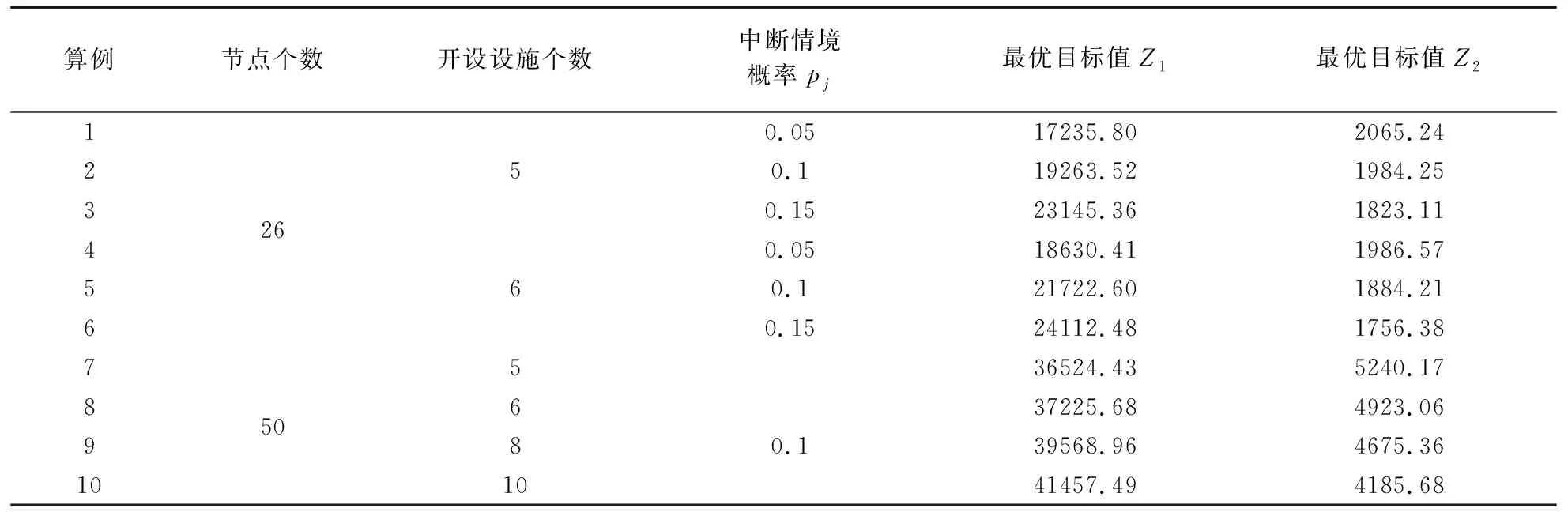
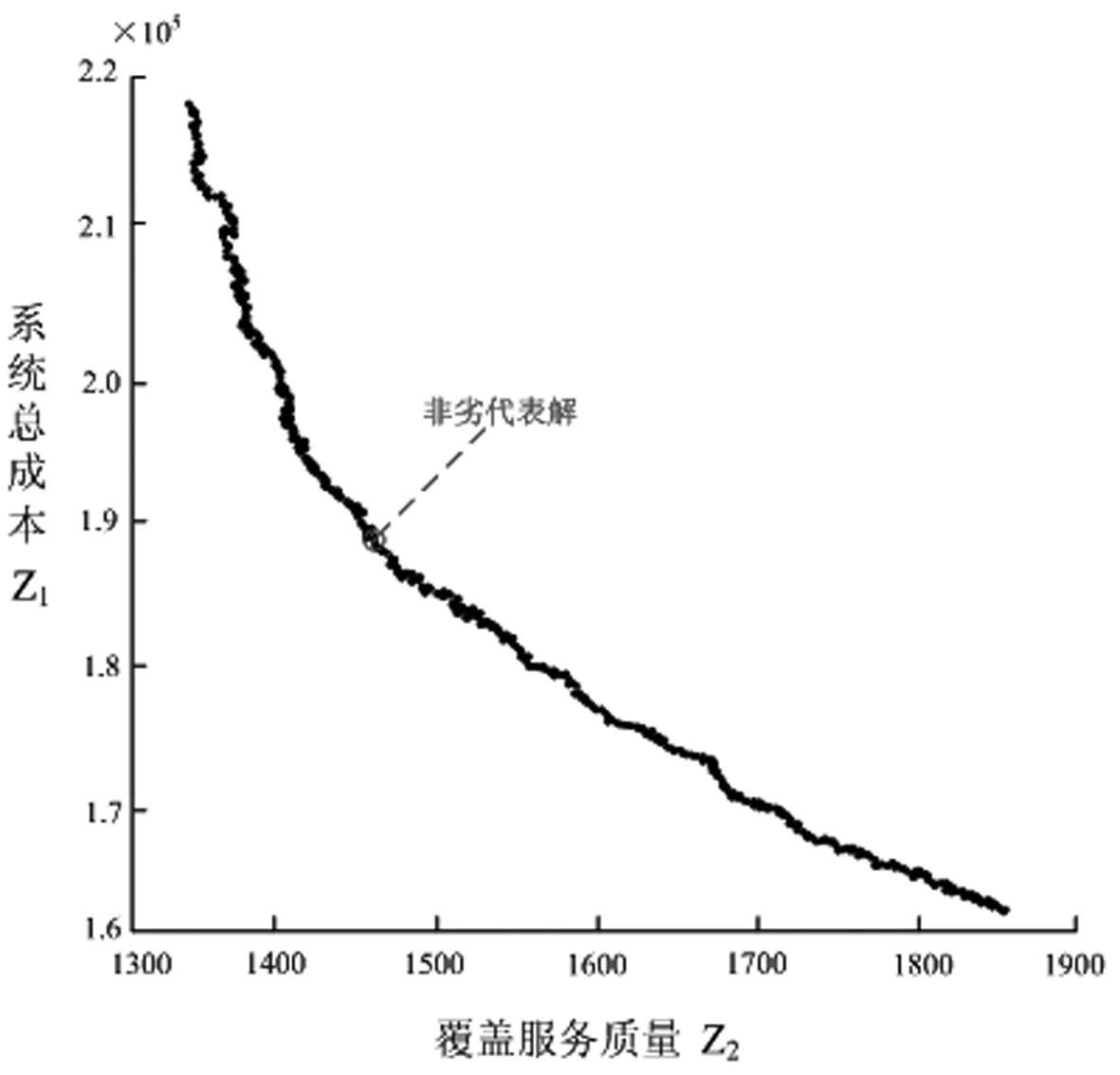
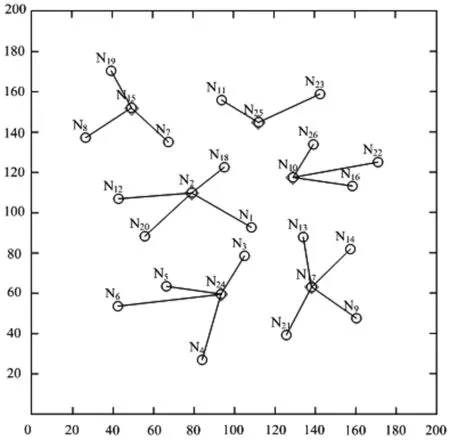
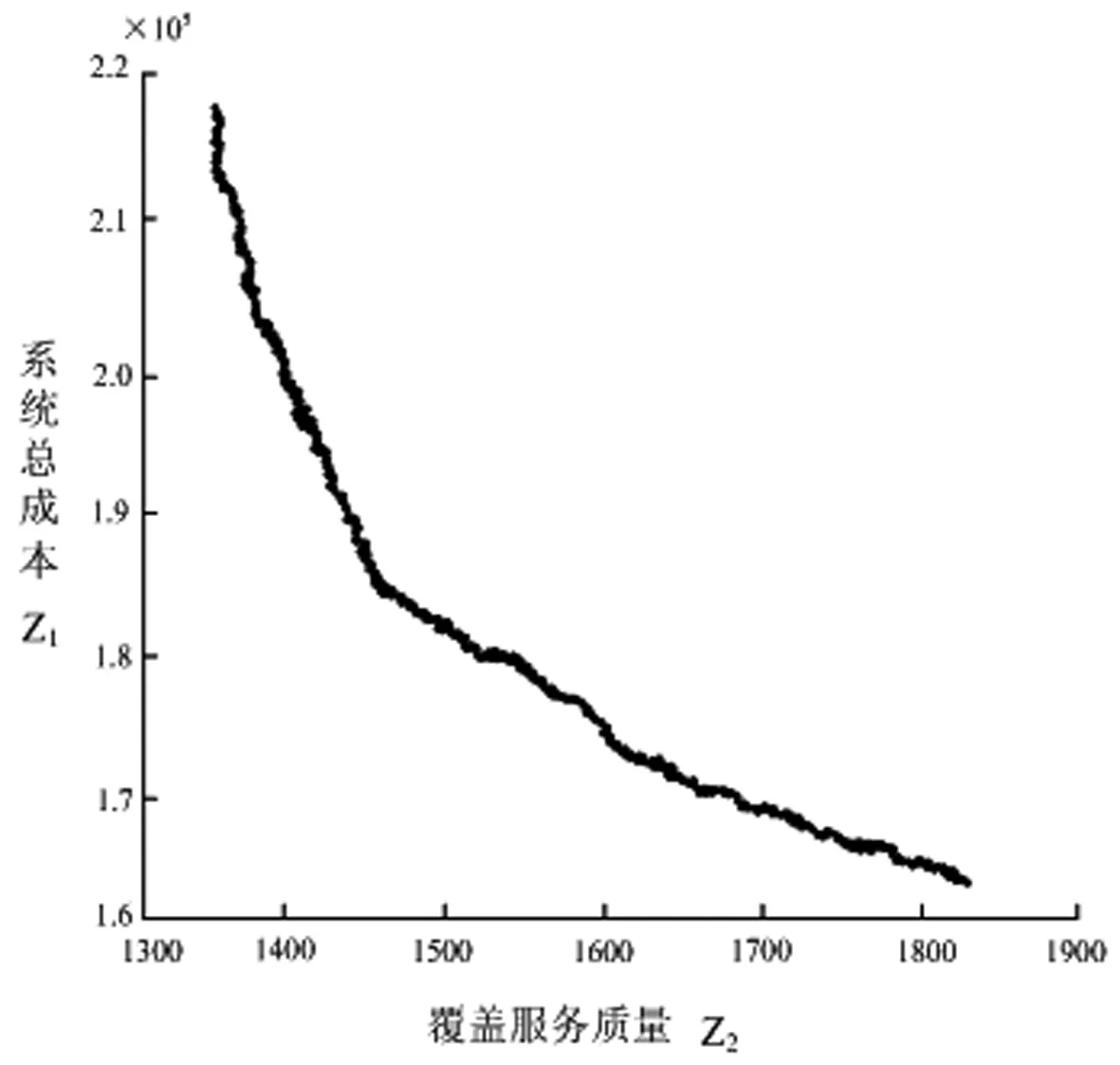
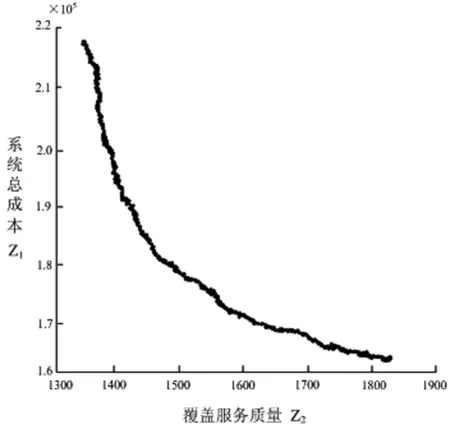
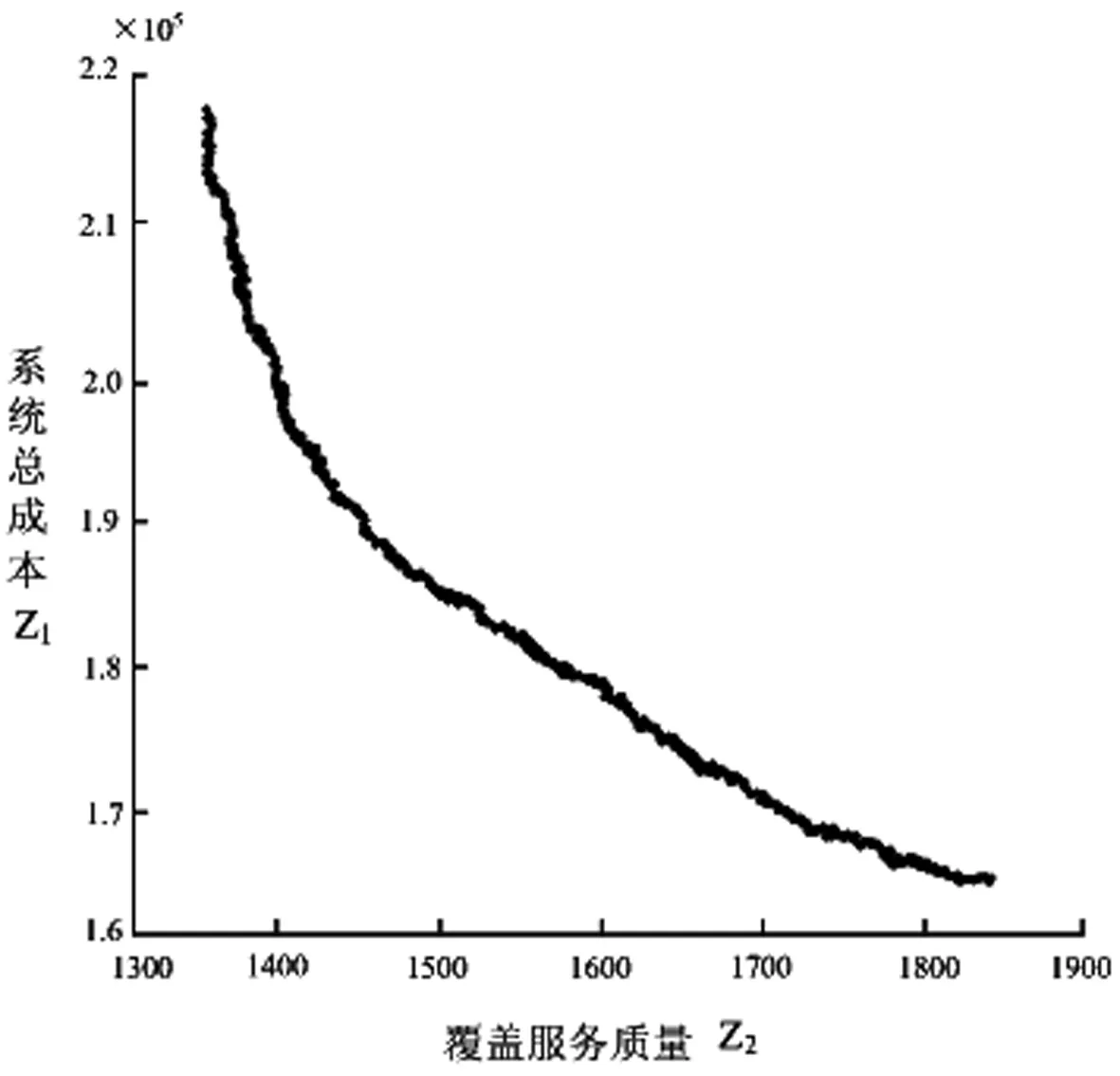
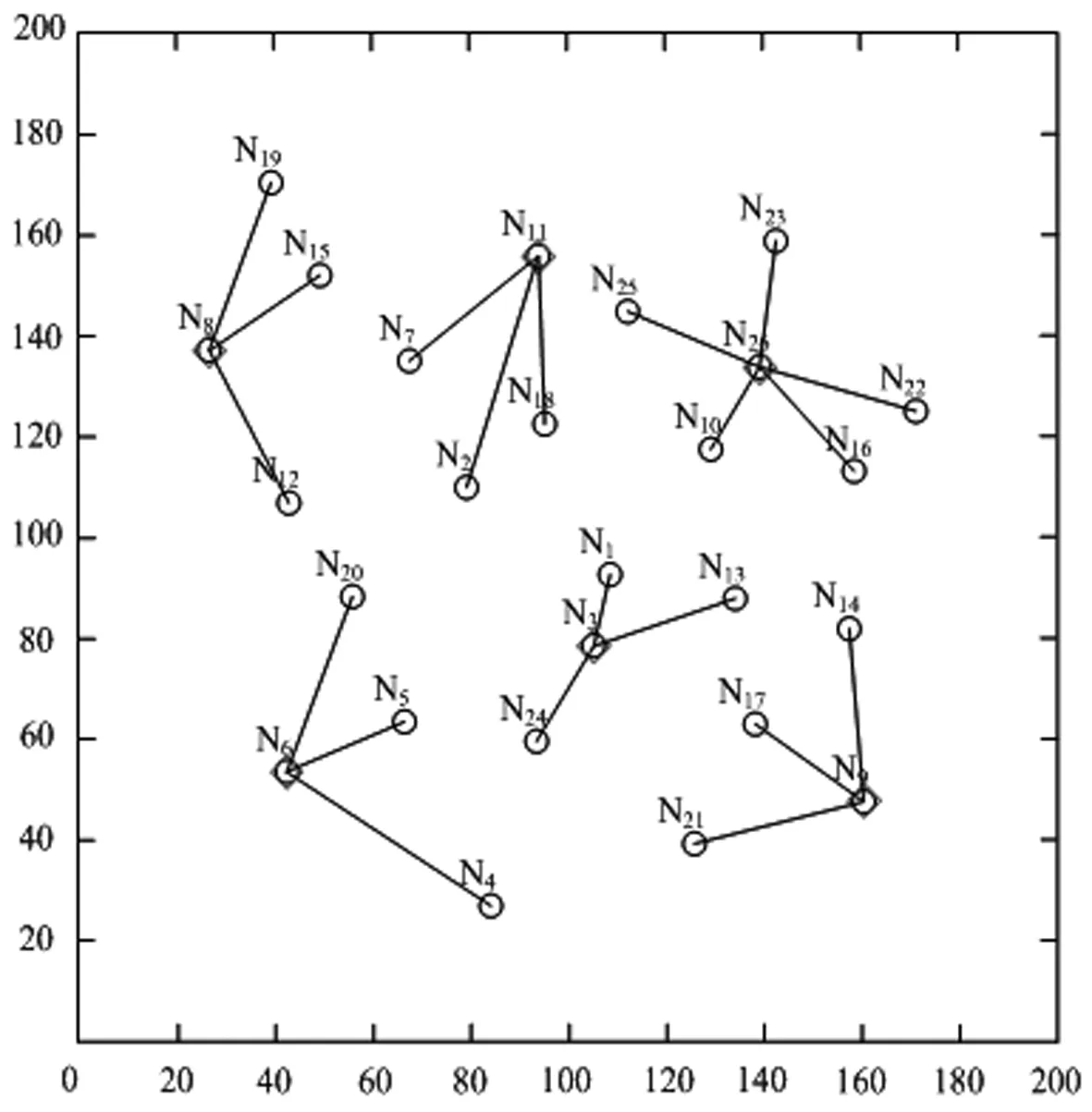
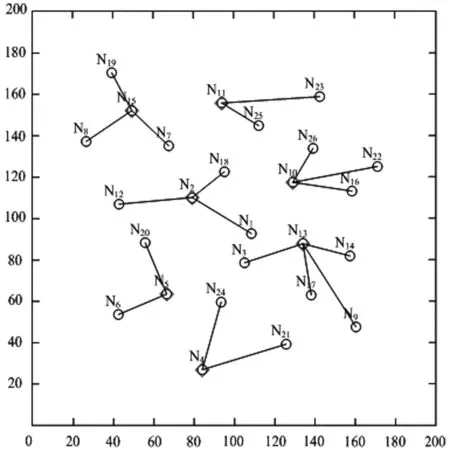
其中,re(re 图1 服务质量敏感程度因子取值不同的函数图像 本文考虑应急设施中断的情境,设N为需求点集合,N={1,2,…,n},i∈N,P为备选应急设施点集合,P={1,2,…,m},j∈P,p为设立应急设施的数量,hi为第i个需求点的应急资源需求,cij为第j个应急设施到第i个需求点的单位需求的运输成本,wij表示第j个应急设施分配给第i个需求点的应急资源量,Ljs,Lju为应急设施的最小和最大容量,d(i,j)为第i个需求点与第j个应急设施之间的距离,qj为第j个应急设施的中断概率,0≤qj≤1,即一个常规的应急设施若在j处建立,则该设施以qj的概率发生中断,fcj为在j处建立常规应急设施的固定建设费用,相应的常规应急设施可基于一定的加固手段使其成为可靠的应急设施,但需提供额外的加固费用,scj为第j个应急设施考虑中断风险的固定投入费用,rcj为第j个应急设施中断时的加固费用,B为应急设施加固费用的预算。xj表示若第j个应急设施设立则为1,否则为0,zj表示若第j个应急设施被加固则为1,否则为0,yij0表示第i个需求点由第j个常规应急设施作为主设施为其提供服务则为1,否则为0,yij1表示第i个需求点由第j个备用应急设施作为主设施为其提供服务则为1,否则为0。 基于上述条件,建立考虑应急设施中断风险的可靠性双目标优化模型。 目标函数为: (1) (2) 约束条件为: (11) 上述多目标优化模型在数学上呈现NP-难的特点,存在不确定数量的非劣解集,相比于单目标决策模型求解最优值,多目标决策的核心问题是在协调多个目标之间的关系,找到一个合理的最优解集,NSGA-II在多目标解空间直接搜索寻优,无需转化多目标为单目标,因其在求解多目标优化问题时的良好的优化效果而得到推广和广泛的应用。本文充分考虑所构建模型的特点,利用NSGA-Ⅱ对所建立多目标优化模型予以求解和决策分析。 考虑应急设施中断风险的可靠性多目标优化模型的求解中,由于目标之间存在不一致性,难以同时达到最优解,一组解集上的任何一个目标值都不可能使自身目标不受损而改善其他目标,因此,目标解集为帕累托最优状态。带精英保留策略的快速非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm Ⅱ, NSGA-II)是印度学者Deb等[18]基于非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm, NSGA)的启发而提出的一种多目标优化算法,该算法作为当前最受欢迎和应用最为广泛的多目标遗传优化算法之一,具有算法计算复杂度相对低,Pareto最优解集收敛效果好、易于编程实现、具有潜在的并行性和分布式等优良特点。已有研究成果表明,NSGA-II较多目标差分进化算法(MODE)、多目标粒子群算法(MPSO)、遗传算法(GA)等具有更好的优化效果[19~23],许多多目标优化算法已将其作为衡量算法性能的测试基准。基于此,本文采用NSGA-II实现所构建多目标优化模型的求解。 NSGA-II通过采用基于分级的快速非支配排序、精英策略、拥挤距离和拥挤度比较算子等策略设计算法和提高算法的性能及优化解的精度[24]。通过权衡模型中两个子目标函数之间的关系,找到使两个子目标都能达到最优的Pareto解集。本文设计算法将种群个体(应急设施点)映射为搜索空间中的点。个体遗传行为操作的过程相当于搜索寻优的过程,个体位置的优劣度量优化的各个目标,可行解集的更新迭代过程突显出个体优胜劣汰的过程。 下面给出NSGA-II求解考虑应急设施中断风险和防御的可靠性双目标优化模型的具体流程。 Step1模型相关参数的设置及初始化:应急设施建立的固定费用fcj,第j个应急设施加固的固定费用scj,第j个应急设施中断时的加固费用rcj,应急设施加固费用的预算B。每个需求点的需求量hi,应急设施的最小和最大容量Ljs和Lju,每个应急设施的中断概率qj,第j个应急设施到第i个需求点的单位需求运输成本cij,覆盖服务质量敏感程度因子k,m,各应急设施覆盖需求点的最小、最大临界距离rs和ru,度量距离的扰动re。NSGA-II中需要设置的参数有:种群规模Ng,最大迭代次数Itermax,交叉概率α,变异概率β。 Step2随机地产生种群规模为Ng的某一个初始种群P0,将其作为父代种群,准备进行非支配排序操作处理。 Step3目标函数适应度值的优化计算与快速非支配排序。计算每一个体相应的分目标适应度值,即求解模型中的两个目标函数值,基于目标函数的适应度值利用快速非支配排序方法进行非劣分层,种群中的个体将被分配到不同的非支配前端集合中。在进行非支配排序分层的同时,基于每一个体的相应分目标适应度值一并计算每个非支配前端集合中个体的拥挤距离,结合目标函数之间的差异值,计算拥挤度值,进而判断一个种群中某个特定解附近的种群密度。拥挤密度越小,则个体目标在该处的分散程度趋于越低,解包围的强度趋于越大,展现出较高的多样性特征。基于二元锦标赛方式随机选择种群中的两个体,比较处于各个非支配前端集合中个体间的拥挤密度,将密度小的对应个体构成种群Ag1。 Step4基于遗传算法(GA)的行为操作。对种群Ag1进行包括交叉和变异的遗传算法行为操作,产生新的个体进入种群中并生成规模为Ng的第一代后代种群Q0。 Step5种群的合并。将父代种群P0和子代种群Q0中的所有个体合并为规模为2Ng的种群P0∪Q0,新的种群记为R0。 Step6计算R0中每个个体相应的分目标适应度值,基于Step3的快速非支配排序方式,进行新一轮排序和非劣分层,同时计算各个非支配分层中个体间的拥挤距离及拥挤度,选择新的最优产生的种群中的个体使之构成新的父代种群P1,基于遗传算法的行为操作依次产生下一代子群。 Step7判断Itermax是否达到预先设定的最大迭代次数,若达到则输出每个个体最优的适应度值和最优个体,反之,迭代次数增加1并跳转执行Step2,直至获得最优的Pareto非劣解集。 为了验证所构建模型及算法的可行性,本文通过随机生成算例进行决策分析,确定最优选址方案和应急资源分配方案,确定拟建应急设施点选址布局网络的拓扑结构,实现需求点的应急资源需求。潜在的应急需求点既作为受灾需求点同时也是候选应急设施点,基于不同规模的节点网络求解多目标优化模型,在相同条件下比较不同中断情境下的选址优化结果,相互权衡确定最优目标值,获得系统经济成本和覆盖服务质量之间的Pareto最优解集,给出Pareto最优解集的分布展示,同时给出应急设施选址布局网络的拓扑结构。以2015a为操作平台,在Intel(R),Core(TM) i7- 6500U CPU,2.50 GHz,8.00 GB内存,Windows10操作系统的PC机上执行算法。 表1 各个应急设施覆盖的最小最大临界距离 在[0,200]×[0,200]的平面区域上随机产生潜在的需求点,应急设施建立的固定费用fcj在[600,800]内随机产生,第j个应急设施抵御中断风险的固定投入费用scj在[200,300]内随机产生,第j个应急设施中断时的加固费用rcj在[150,200]内随机产生,应急设施加固费用的预算B在[2000,3000]内以随机方式产生,每一需求点的需求量hi在[90,120]内随机生成,应急设施的最小和最大容量Ljs和Lju在[80,120]和[450,600]内随机产生,第j个应急设施到第i个需求点的单位需求运输成本cij在[6,8]内随机产生,中断概率pj在[0.1,0.5]内随机产生,覆盖服务质量敏感程度因子k=0.5,m=0.1,度量距离的扰动re在[0.1,0.5]内随机产生。相应需求点的最小临界距离和最大临界距离见表1。设置种群规模Ng=100,交叉概率α=0.8,变异概率β=0.01,最大迭代次数Itermax=300。 首先,基于NSGA-II求解考虑应急设施中断风险的可靠性选址模型,基于算例的不同规模,获得10组算例的优化结果见表2。 表2 不同算例规模下的选址优化结果 从优化计算的结果可以看出,对于不同规模选址网络的算例,随着需求点规模增加及拟建应急设施数量的增加,选址的总成本随之增加。在规模(节点个数)及其他参数设置相同的情况下,应急设施中断概率的变化对最优选址方案的影响显著,应急设施中断概率增大时选址的总成本逐渐增加,覆盖服务质量降低,两个目标函数之间呈现此消彼长的关系,获得系统经济成本与覆盖服务质量之间的均衡。由此可见,当决策者考虑应急设施中断风险趋于乐观时,设计的选址-分配网络更精益,总成本相对较小,而当始料未及的灾害事件发生时,网络将会受到较大的冲击,因此,决策者可以基于不同的风险偏好和决策目标在节约成本和提高服务质量之间权衡。 以算例6为例,针对26个潜在需求点,拟建立6个应急设施的选址节点网络,以可视化的形式给出选址布局决策的Pareto前沿,算法经过300次的迭代寻优,所构成的Pareto最优前沿如图2所示。 图2 Pareto最优前沿和非劣代表解 图3 应急设施选址-分配网络的拓扑结构 下面分析应急设施中断对选址-分配决策的影响,考虑不同的应急设施中断概率,基于上述26个节点网络确定6个应急设施的选址布局决策,首先以可视化的形式给出不同中断概率下目标空间内的Pareto解最优前沿的分布展示,如图4~7所示。 图4 pj=0.05时Pareto最优解集的分布 图5 pj=0.1时Pareto最优解集的分布 图6 pj=0.15时Pareto最优解集的分布 图7 pj=0.2时Pareto最优解集的分布 如图所示的Pareto非劣解集类似空间中的一条不连续分布的曲线,其函数图像曲线上的每个点代表多目标选址模型的一个非劣解,且相应的解集中的各个非劣解之间没有好坏解之分,该曲线由124个非劣解在目标空间相对较均匀分布而成。在所得Pareto最优解集中,目标函数之间呈现此消彼长的关系。从函数图像可以看出,系统的总成本、期望服务质量水平两个目标之间是相互对立和相互关联的,当某一个目标函数值发生变化必将引起另一个目标函数值的变化。函数图像曲线上的各点是两个目标函数值的非劣组合,当选址决策的目标趋向于成本控制的视角考虑时,则在曲线中靠近目标函数z1的左上半支中选择相对折中的解,当选址决策的目标更趋向于服务质量水平较好的视角考虑时,则在曲线中靠近目标函数z2的右下半支中选择相对折中解,但会以付出较高的系统成本为代价。 进一步以可视化的形式给出不同中断概率下的应急设施选址-分配网络的拓扑结构。基于上述26个节点网络,利用NSGA-II确定6个应急设施的选址布局决策和应急资源分配决策,在不同的中断概率下,应急设施选址-分配服务网络的拓扑结构如图8~11所示。 以上通过对应急设施中断的情形以不同的概率大小进行刻画,获得不同的选址-分配方案。图中小圆形表示需求点的位置,菱形表示应急设施点的位置,菱形与小圆形之间的连线表示对应的应急资源分配。不同的中断概率使应急设施选址-分配网络的拓扑结构截然不同,各应急设施点在不同的选址网络拓扑结构下服务分配发生改变。在抵御中断风险和进行多目标决策时,决策者需基于不同的中断风险偏好和具体实际在成本经济性和覆盖服务质量可靠性之间作出相应的权衡,由此确定应急设施的选址-分配方案。 图8 pj=0.05时选址-分配网络的拓扑结构 图9 pj=0.1时选址-分配网络的拓扑结构 图10 pj=0.15时选址-分配网络的拓扑结构 图11 pj=0.2时选址-分配网络的拓扑结构 本文考虑应急设施的中断风险,基于应急设施的系统成本最小化及覆盖服务质量最大化,在考虑应急设施中断时的加固预算有限的前提下,均衡多重约束条件建立可靠性多目标选址布局决策模型,基于模型特点利用NSGA-Ⅱ实现对模型的优化求解,并通过随机生成的数值算例验证模型和算法的可行性,获得不同规模的可行度较高的多目标选址模型的Pareto非劣解集。基于不同的中断概率进行灵敏度分析,分别获得Pareto最优解集的分布,同时给出应急设施选址-分配网络的拓扑结构,以利于决策者基于不同的风险偏好在Pareto前沿面上获得最优的选址分配方案。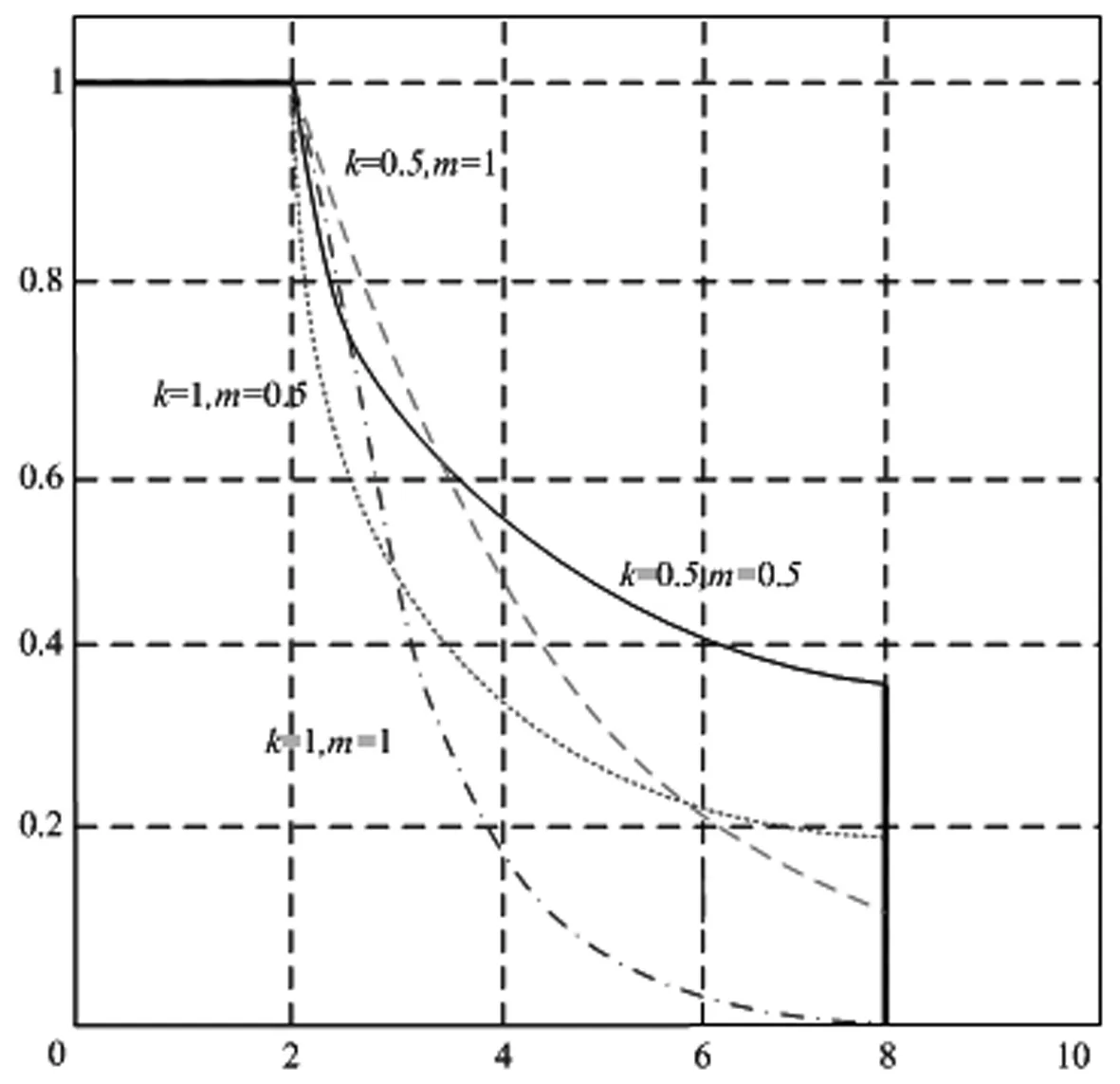
1.2 数学模型
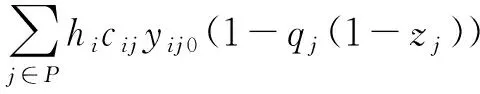
2 模型求解
3 算例分析




4 结论

