基于前景理论的混合不确定情景下在线多属性反向拍卖的赢者确定方法
王世磊, 屈绍建, 刘志敏, 马 刚
(上海理工大学 管理学院,上海 200093)
0 引言
拍卖,作为一种市场机制,其主要是根据市场参与者的投标来决定资源的分配和价格的设定[1]。拍卖在当今的经济社会发展中扮演了越来越重要的角色,它越来越多地应用于工业采购、供应链管理、电子广告、服务分配和电子商务等诸多领域。正如在2000年世界计量经济学大会的受邀报告中Klemperer[2]所指出的:“拍卖是主流经济学的一部分,每个经济学家都应该学习一些拍卖理论”。拍卖理论不断被广大学者所接受并得到了广泛地拓展研究,这其中著名诺贝尔经济学奖获得者Vickrey在1961年发表的论文《Counter-speculation, auctions and sealed tenders》被认为是拍卖理论研究的开山之作。随后,很多著名的学者如Riley、Samuelson、Myerson、Milgrom等都对拍卖理论进行深入研究与拓展[3]。随着互联网技术及电子商务的快速发展,网络拍卖日益成为一种流行且重要的市场交易方式。如国外的知名网购平台eBay、Yahoo、Amazon都有自己的拍卖网站,在国内也有如易趣网、一拍网和淘宝拍卖等拍卖网站。与此同时,网络拍卖的成交额也日益增加,使得在线拍卖成为当前拍卖领域研究的前沿和热点[3]。然而,早期关于传统拍卖与在线拍卖的研究较多仅以价格来确定中标者及拍品的分配,而对于产品质量、交货期、质保期等重要的非价格因素缺乏考虑,而这从不同程度上影响了拍卖的最终效果。从而促使了在线多属性拍卖[4]的产生,其主要采用在线多属性采购拍卖(OMARA)的形式,即:一个采购方(买家)在线发布所需采购商品的价格属性和其他非价格属性的要求,若干感兴趣的供应商(卖家)参与竞争投标,最后采购方确定最终获胜者的整个过程。
Che在文献[5]中首次较为系统地研究了多属性(采购)拍卖,他证明了二维情形下的收入等价原理( revenue equivalence theorem ),把一级和二级价格密封式拍卖推广到多属性拍卖领域,并基于买方知悉卖方的成本参数的概率分布的假设下设计了最优评分规则,构建了一个二属性采购拍卖模型。Branco[6]推广了Che的工作,在投标者成本函数相关联的条件下,基于社会福利最大化设计了最优拍卖机制。沿着Branco和Che的研究思路,David[7]等人的一系列工作先后将两属性拍卖推广到三个属性和任意多个属性的情形。此外,从实验经济学方法角度,Bichler[8]对多属性拍卖和传统的单一价格拍卖进行了实验比较研究,结果表明多属性拍卖既增加了买方的效用,也增加了卖方的利润。综合相关文献[9~12]可以看出多属性在线反向拍卖广泛应用于政府采购、电力行业、工程招标、IT行业、能源、电子商务等多个行业,其重要性也越来越凸显。目前(在线)多属性反向拍卖主要从博弈论和决策论两个大方向进行建模和分析[12],前者主要从经典经济理论和不完全信息博弈角度进行研究买卖双方的均衡策略分析,得到最优拍卖机制[13,14];后者多以多属性决策(MCMD)经典方法为指导进行产品属性设置及最终竞胜供应商的确定。目前,关于供应商的赢者确定的定量方法主要有层次分析法(AHP)[15]、逼近理想解的排序方法(TOPSIS)[16]、数据包络分析(DEA)[17]、模糊综合评判法[18~20]、层次交互式决策方法[21]和偏好顺序结构评估法(PROMETHEE)[22]等。本文我们主要是从决策论角度来研究采购方在OMARA中关于最优竞标供应商的确定问题。
OMARA的实施对于采购方和供应商来说是都存在一定的挑战,采购方需要考虑如何确定自己的最优采购商品属性的权重分配,如何构建能实现自身需求的恰当评价函数[7];供应商则要根据自身情况和买家的评价函数形成最优投标,以增加获胜的几率并最大化利润[17]。在实际采购活动中,由于采购方对整个市场供应商产品的价格、质量等属性信息重要程度不能确切把握,而且有些属性不宜直接用精确数字进行描述,加之采购方对风险的偏好差异等模糊不确定因素的存在,使得采购方在确定属性权重和选择评价策略时难度增大。
当前,关于不确定情形下多属性反向拍卖供应商选择问题相关的研究文献中:有考虑单一属性值表述方式的,如文献[18~20]分别研究属性值用粗糙集、三角模糊数和区间模糊表述的情形;有研究存在多种属性表述方式的,如文献[23,24]研究了同时存在精确数、区间数、三角模糊数三种表述方式的情形,文献[25]研究了同时存在精确数、区间数与语义短语三种表述方式的情形,它们也都给出了相应的决策制定方法。然而,同时存在精确数、区间数、三角模糊数、梯形模糊数、语义模糊术语五种描述方式的混合不确定情形下的OMARA供应商确定问题的研究目前尚缺乏。为了拓展和完善相关的研究内容,本文通过引入上述五种描述方式对OMARA中投标者的投标属性进行刻画;同时考虑到采购方的风险态度而引入了前景理论[23~26],构建了一种新的基于模糊理论与前景理论的混合不确定情形下的OMARA的竞胜供应商确定方法,该方法相较于前面所提文献中的方法更具有一般性和适用性,而且在实际运用中简单易行。最后,结合OMARA的具体算例进行方法展示与分析,并与之前的研究结果进行比较,验证了本文所给出的方法的可行性和有效性;同时,还进行了相关的稳健性分析研究,进一步地表明了本文所提的OMARA赢者确定方法在处理相关的混合不确定情形时具有明显的稳定性与适用性。
1 预备知识
本节我们主要介绍与本文研究相关的一些基础知识,主要包括区间数、三角模糊数、梯形模糊数、语言模糊术语集的定义,以及相关的距离定义和运算规则;同时还介绍了前景理论的相关定义。
1.1 区间数

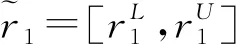
(1)
1.2 三角模糊数

(2)

(3)
1.3 梯形模糊数
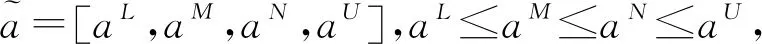
(4)

(5)
1.4 语义模糊术语集
定义7[25]设S是语义模糊术语集,则其形式可表示为:S={sk|k=0,1,…,T},其中sk表示s中第k+1个语义模糊术语,即元素都是用语义进行表达。
T一般取偶数,例如,当T=4时,有S={so,sj,…,s4},可以分别对应“很差、差、中等、良好,很好”五种语义模糊术语。为了便于语义模糊术语的处理与计算,一般可以将它们转化成三角模糊数的形式,具体方法如(6)式所示:

(6)
S中常存在两种算子:1) 比较算子:si≥sj,若i≥j;2) 否定算子:neg(si)=sj,若j=T-i。
1.5 前景理论
在实际采购活动中,当采购商和供应商在面临信息不确定与潜在风险时,他们的决策行为一般都是不完全理性的。为了解决这个问题,Kahneman[27]等人于1979年提出了前景理论,主要内容包括价值函数和决策概率权重。价值函数主要用于刻画属性值相对于参照点的损失和增益情况,可表示为:
(7)
其中,0<α,β<1,分别表示风险厌恶和风险偏好的系数,θ>1表示损失规避系数,说明决策者对损失表现的更加敏感。当α=β=θ=1时,价值函数退化为了一般的线性效用函数,即为:v(x)=x,它无法充分体现决策者风险态度对其效用的影响。根据文献[28]的研究结果,我们在本文中选定α=β=0.88,θ=2.25。
设ω是属性的决策概率权重,则各供应商投标中所有属性的综合前景价值可表示为:
U=∑ω·v(x)
(8)
2 在线多属性反向拍卖的赢者确定问题描述
在本文的模型中,假设存在一个风险规避的采购商以在线反向拍卖方式采购一定数量的某种商品,存在m个感兴趣的供应商参与竞标。采购商在发布采购招标信息中说明了商品的价格属性指标和若干非价格属性指标,以及对供应商信誉等方面的属性要求(假定总属性个数为n)。供应商根据自身情况及采购者需求确定各项属性值,并提交标书参与竞标。最后采购者根据设定的评价标准,对供应商进行筛选和测评,评价值最高者最终胜出,随后采购者与之签订相关采购协议。具体可用以下多元组来描述整个在线多属性反向拍卖赢者确定问题(OMARA-WDP):
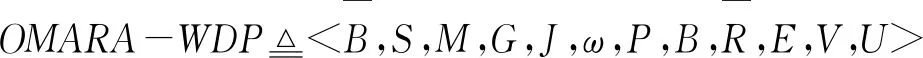
(9)
具体符号的含义介绍如下:

2)S表示供应商集合,S={s1,s2,…,sm},si表示第i个供应商,i∈M,M={1,2,…,m}为S的指标集;
3)G表示采购商提出的全部属性的集合,不同属性可以由不同形式进行表示,G可以表示为如下形式:G={G1,G2,…,Gn}=GN∪GI∪GTri∪GTra∪GI=GB∪GC,其中GN表示属性用精确数表示的属性集合,GL表示属性用区间数表示的属性集合,GTri表示属性用三角模糊数表示的属性集合,GTra表示属性用梯形模糊数表示的属性集合,GL表示属性用语义模糊术语表示的属性集合,GR表示成本型属性的集合,GC表示效益型属性的集合;
4)J表示所有属性的指标集,其可以表示为J={1,2,…,n}=QN∪QI∪QTri∪QTra∪QL=QB∪QC,其中QN代表集合GN的指标集,QI代表集合GI的指标集,QTri代表集合GTri的指标集,QTra代表集合GTra的指标集,QL代表集合GL的指标集,QB代表集合GB的指标集,QC代表集合GC的指标集;
5)ω表示采购方对各属性的预期权重向量,且ω={ω1,ω2,…,ωn},ωj表示第j个属性的权重;
6)P表示所有供应商提交的竞标属性值构成的评价矩阵,记P=[pij]m×n,其中pij表示供应商i的投标对第j个属性的评估值;
7)B表示规范化后的评价矩阵,记B=[bij]m×n,其中bij表示供应商i的投标对第j个属性的评估值;
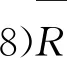
9)E表示规范化后的评价值参考点向量,记E=(e1,e2,…,en),其中ej表示对第j个属性的参考值;
10)V表示前景值矩阵,记V=[v(bij)]m×n,其中v(bij)表示第个供应商投标对第j个属性的前景值;
11)U表示累积前景价值。
注1在本节和后文中,为了书写方便、整齐,我们对精确数和其他模糊数的书写上未做明显区分,但在描述和计算时都会明确说明每个元素(属性值)的表述方式。
3 混合不确定情景下OMARA赢者确定方法
基于上节OMARA-WDP的描述,本节给出一个新的混合不确定情形下的OMARA赢者确定方法,具体过程如下:
3.1 构建初始评价矩阵和参考点向量
采购商在线发布采购信息,给出具体的供应商及其产品的相关属性要求和投标模板,由于存在多种不确定情形,属性评估值允许用不同形式进行刻画,本文假定同时存在精确数、区间数、三角模糊数、梯形模糊数、语义模糊术语五种表述方式,且指定对于每一种属性评价值(即矩阵中的每一列元素)采用同一种表述方式;然后m个合规的兴趣供应商在规定的投标期限内投标,之后采购商将所有投标信息进行汇总整理,构建出初始评价矩阵P:
G1G2…Gn
(10)
(11)
3.2 规范化评价矩阵和参考点向量
根据不同属性的刻画方式不同,下面分类型对评价矩阵和参考点向量中元素进行规范化处理。一般文献如[20,24],主要采用简单的极差变换法,他们在做规范化处理时只是对属性值进行处理,而参考点向量一般单独主观给定,这种方法存在主观性过强,且后期距离计算时误差较大的不足;而本文受文献[25]的启发,同时根据供应商的投标属性值客观地选取参考点向量,所以同时考虑两者的规范化,能使得计算结果更加客观和精确。具体操作如下:
(1)当属性Gj∈GN时,属性值用精确数表达,则相应属性值的规范化公式为:
(12)
参考点向量对应元素规范化公式为:
(13)
(2)当属性Gj∈GI时,属性值用区间数表达,则相应属性值的规范化公式为:
(14)
参考点向量对应元素规范化公式为:
(15)
此处分别为:
(3)当属性Gj∈GTri时,属性值用三角模糊数表达,则相应属性值的规范化公式为:
(16)
参考点向量对应元素规范化公式为:
(17)
此处H1,H2分别为:

则相应属性值的规范化公式为:
(18)
(4)当属性Gj∈GTra时,属性值用梯形模糊数表达,参考点向量对应元素规范化公式为:
(19)
此处H1,H2分别为:

(5)当属性Gj∈GL时,属性值用语义模糊术语表达,则相应属性值的规范化公式为:
(20)
参考点向量对应元素规范化公式为:
(21)
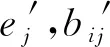
综合上述处理过程,我们可以得到规范化后的评价矩阵和参考点向量,分别为:
G1G2…Gn
(22)
E=(e1,e2,…,en)
(23)
3.3 计算各供应商投标属性值的综合前景值
经过3.2节数据规范化处理后,本小节我们主要介绍如何计算各供应商投标方案中属性值的累积前景值,具体步骤如下:
(1)计算属性值bij与参考点ej的距离

(24)
(2)比较属性值bij与参考点ej大小
1)当属性值都用精确值表述时,直接比较大小即可;
2)当属性值都用区间数表述时,按区间数比较方法[25],记:
a)当h(bij)≠h(ej)时,若h(bij)>h(ej),则bij>ej;若h(bij) b)当h(bij)=h(ej)时,若k(bij)>k(ej),则bij 3)当属性值都用三角模糊数表述时,利用模糊概率及期望值方法[29]比较大小,记: 若z(bij)>z(ej),则bij>ej;若z(bij)=z(ej),则bij=ej;若z(bij) 4)当属性值都用梯形模糊数表述时,采取与三角模糊数类似方法进行大小比较: 若z(bij)>z(ej),则bij>ej;若z(bij)=z(ej),则bij=ej;若z(bij) 5)当属性值用语义模糊术语表述时,由定义7和公式(6)可先将其转化成三角模糊数,然后再按3)的方法进行大小比较。 (3)构建投标属性值的前景值矩阵 基于前景理论构建供应商对每个投标属性值的前景值矩阵V=[v(bij)]m×n,其中v(bij)表示第i个供应商投标方案的第j个属性的前景值,有如下形式: (25) 当bij≥ej意味着相对参考点获得增益,而当bij (4)确定各投标属性的权重 属性的权重表示属性的相对重要程度,本文我们采用类似文献[30]方法的最大偏差法来计算属性权重,相较于文献[26]中属性权重求解方法过于复杂,本文提到的方法更简单易行。属性值偏差越大,属性权重就越大。属性权重的计算公式如下: (26) 上式中距离d(bij,bkj)的计算采用欧式距离公式(1)、(3)、(5)进行,对于采用其他形式的距离公式会对属性权重产生何种影响,我们将在第5.2小节中进行具体分析。 (5)计算各供应商投标属性值的综合前景值 (27) 采购商根据各供应商在线投标中各属性值的累积前景值Ui,按在线评价程序对供应商进行从低到高排序,排名最高的供应商被选定为最终获胜者;采购商在线发布获胜者信息,与之进行后续采购合同的签定,整个OMARA结束。 基于以上分析,下面将OMARA获胜供应商确定方法步骤概括如下: 第1步采购方在线发布采购拍卖商品的名称、数量、结束时间等基本信息,主要说明对供应商本身有关属性要求以及提供产品的成本型属性和效益型属性的基本要求; 第2步兴趣供应商根据自身情况和采购方要求,在规定时间内在线提交各自标书,根据不同属性信息分别用精确数、区间数、三角模糊数、梯形模糊数、语言模糊术语进行属性值表述; 第3步根据投标信息对供应商进行资格筛选,排除不合格投标的供应商,合格供应商进入投标方案评价阶段; 第4步采购方以所有合格供应商的投标信息为基础,制定初始评价矩阵P; 第6步将评价矩阵和参考点向量按照公式(12~23)进行规范化得到评价矩阵B和参考点向量E; 第7步基于规范化后参考点向量和评价矩阵,按照公式(24~25)计算每个供应商对采购商品不同属性投标值的前景值,并构建前景价值矩阵V; 第8步根据对整体属性的评估,基于最大偏差法,根据公式(1)、(3)、(5)、(26)计算各属性的权重ωj; 第9步由公式(27)计算每个供应商的投标方案关于所有属性的综合前景值Ui; 第10步采购方选择投标方案综合前景值最高的供应商作为最后的获胜者; 第11步在线发布最终获胜供应商信息,并与之达成最终采购合同或协议,整个在线多属性采购拍卖结束。 假设某一食品加工企业(采购方)欲采购一定数量的某种原材料产品,其通过某拍卖网站在线发布相关招标信息,对产品和商家的属性要求进行描述。这里,假设采购商选取5种属性:{G1,G2,G3,G4,G5},假设五种属性之间相互独立,其中G1表示“产品保质期”,该属性值用精确数表述,一般描述为‘几个月或者几年’,本文统一用月数表述;G2表示“产品单价”(设单位为‘元’),该属性值用区间数数表述,即供应商允许采购价格在某一指定价格范区间围协商;G3表示“产品交货时间”,该属性值用三角模糊数表述,一般描述为“一般情况下多少天,也有可能提前或滞后几天”;G4表示“产品质量动态评分”,该属性值用梯形模糊数表述,一般随机选取历史四个时间点的评分值构成一个梯形模糊数,并假定最高评分为10,最低为0;G5表示“供应商历史信誉”,该属性值用语义术语表述,可从第三方评级机构获得,这里可描述为‘差、较差、一般、较好、好’五种语义形式。其中属性G1,G4,G5于效益型属性,属性G2,G3属于成本型属性。假设存在4个合规的兴趣供应商,并假定供应商对各属性偏好独立,且互相之间不存在共谋情况。 采购方按照本文第3节所给的具体方法进行竞胜供应商确定,详细过程如下: Step1供应商按照采购商的相关要求,在规定时间内进行了在线投标; Step2采购方在线收集供应商的投标信息,筛选合格供应商(假设4个投标供应商均通过资格筛查),根据他们的投标信息制定初始评价矩阵P为: G1G2G3G4G5 Step3将P中属性G5的语义描述从上到下按定义7转化成三角模糊数,分别对应为:[0.75,1.1],[0.25,0.5,0.75],[0.25,0.5,0.75],[0.5,0.75,1]。 表1 规范矩阵B和规范参考点向量E 表2 属性值与参考点间距离 Step7根据公式(25)构建供应商投标属性值的前景值矩阵V=[v(bij)]m×n(如表3所示): 表3 前景值矩阵 Step8基于最大偏差法,根据公式(1)、(3)、(5)、(26)计算各属性的权重ωj(如表4所示): 表4 属性的权重 Step9基于公式(27)计算每个供应商投标中各属性值的综合前景值Ui(如表5所示): 表5 综合前景值 Step10选择综合前景值最高的供应商作为最后的获胜者,并在线发布获胜者信息,采购者与获胜供应商达成采购合同或协议。 由Step 9的计算结果可知,综合前景值大小关系为:U1>U4>U3>U2,所以对于采购商来说,对4个供应商的偏好顺序为:s1≻s4≻s3≻s2,所以供应商s1成为最后的竞胜者,达成采购合同或协议后,拍卖结束。 由上述结果分析,可得到如下几点认识: 1)由s1成为最后的获胜者,可以看出“供应商的历史信誉”对采购商的决策起到了至关重要的影响作用,这与实际网购中购买者非常看重产品商家的信誉度保持一致; 2)由表4可见价格属性的权重最大,说明对于采购商而言,价格属性的考量仍然处于非常重要的位置,因为这与采购商的预算密切相关; 3)供应商产品的“质量”高低对采购商的决策影响比重较大,说明采购商的决策时不在仅考虑价格属性,质量属性的影响也至关重要; 4)在其他属性差别较小时,容易看到“产品交货时间”对采购商来说也凸显了其重要性,特别是对于易腐农产品、生鲜食品类产品的采购影响更为凸显。 注意到文献[31],Weber等人对1966年至1990年发表的74篇关于多属性采购的相关文章进行了回顾和分类,并对这些文章中研究的所有属性进行了排序,他们得出结论:价格、质量、交付时间是最为重要的几个评价属性。易见,由上述算例我们得到的几点认识和Weber等人的研究结果基本吻合,从而说明本文提出的采购拍卖获胜者确定方法是可行的。 下面进一步通过比较来说明本文所提方法的有效性。由于目前还没有同时考虑本文中所给出的五种属性描述方式的反向拍卖文献,所以本文参考文献[29]的处理方法,将所有模糊数全部解模糊化为精确数,然后将它们看成左右端点值等于中点值的三角模糊数,然后再用文献[32]方法进行计算和排序。 首先,将原初始化转化为仅含三角模糊数描述的决策矩阵,并确定正、负理想点向量(如表6所示); 表6 三角模糊数型决策矩阵以及正、负理想点向量 表7 投标方案与正理想解方案相对贴近度 为了进一步检验本文所给赢者确定方法在不同的情形下的决策效果,现进行如下两个方面的稳健性分析。 为了观察当投标属性值存在较大差别时,会对属性前景值、属性权重以及最终的采购商偏好排序结果产生何种影响,我们在本小节对不同供应商投标方案中部分属性值(产品单价)进行数量级上的改变,然后再运用本文提出的多属性反向拍卖的赢者确定方法进行计算和排序,观察结果的变化情况。采购方根据供应商投标信息按照第3节所给的方法进行竞胜供应商的确定,具体过程如下: Step-1过程同第4节的Step 1; Step-2过程同第4节Step 2,但得到新的评价矩阵: G1G2G3G4G5 Step-3过程同第4节的Step 3; Step-6根据公式(24)计算每个属性值与参考点向量对应元素的距离dij″; Step-7根据公式(25)构建供应商投标属性值的前景值矩阵V′;(由于Step-5~Step-7与第4部分过程一致,故此处的具体计算结果不再详细展示) 表8 各属性的权重 表9 投标综合前景值 本小节我们引入了三种距离计算公式:海明(Hamming)距离[33]、曼哈顿(Manhattan)距离[34]和切比雪夫(Chebyshev) 距离[35](将它们对应简记为:dham,dmht,dcbv),将它们分别带入公式(26)中重新计算第五节算例中的各方案的属性权重值,及最终的综合前景值与方案排序,并于与本文所选的(Euclidean)距离(deuc)公式结果进行对比分析,各种情形下属性权重值的结果如表10所示。 表10 不同距离公式下投标属的权重变化 结合表3和表10,计算得到不同距离公式情形下各供应商投标的综合前景值(具体见表11): 表11 不同距离公式下各供应商投标综合前景值 基于以上,可得不同距离公式情形下采购商对各供应商的偏好排序结果(见表12)。 基于表(10)~(12)的结果,可见采用不同的距离公式,各供应商的投标方案综合前景值大小发生了较小的变化,最终的偏好排序结果也出现一定程度的变动。主要变化发生在海明(Hamming)距离公式下供应商S1和S4的排序上,说明了不同距离公式下确实会对模糊数的计算产生一定的影响;而在曼哈顿(Manhattan)距离公式和切比雪夫(Chebyshev)距离公式情形下的最终排序结果都与本文所选的欧氏(Euclidean)距离情形下的排序结果保持一致,这也侧面反映出大多数模糊决策文献(如[24~26,29,32])选择欧氏(Euclidean)距离公式的缘由。同时,通过采购商针对供应商赢者确定偏好排序结果的比较,进一步说明了本文所提的在线多属性反向拍卖的竞胜供应商确定方法是稳健、有效的。 表12 不同距离公式下采购商对各竞标供应商的偏好排序 考虑到多属性反向拍卖实际中存在的商品属性和商家信息的不确定性,以及采购者的风险态度和有限理性特征,本文我们主要从采购者角度出发,充分利用前景理论和模糊理论知识,研究了混合不确定情境下OMARA的竞胜供应商确定问题,提出了一套更具一般性的赢者确定方法,并结合具体的算例分析、对比分析和拓展性研究,验证了所提方法的合理性和有效性,丰富了现有的多属性反向拍卖的研究内容。然而,在互联网、电子商务不断普及的当下,虽然越来越多的国内外企业都开始采用网上反向拍卖来节约成本,但OAMARA的理论发展还远没有达到它应有的程度,特别是国内相关研究还很薄弱,这从侧面反映出这一领域研究的重要性和紧迫性。基于本文研究的不足及未来可能的研究方向作如下几点展望: (1)本文仅在同时存在五种属性表述方式的情形下利用前景理论和模糊理论来研究在线多属性反向拍卖的竞胜供应商确定方法,对于其他类型的模糊数表述形式(如直觉模糊数、犹豫模糊数等)或者更多表述形式的混合不确定情景下的竞胜供应商确定方法值得进一步地研究; (2)如何利用实际采购拍卖数据进行实证分析来进一步验证方法的适用性也是值得研究的问题; (3)如何结合计算机网络、智能技术,构建基于多Agent的自动化采购招标平台,实现实时动态的拍卖机制,将会给采购拍卖供求双方带来成本的节约,且提高了交易的效率,这一模块值得进一步地研究; (4)如何较好地将经典效用理论、博弈理论、优化理论、决策理论、模糊理论与拍卖理论结合起来,为后续的OMARA理论研究与实践应用服务,值得未来长期深入地研究。3.4 确定获胜供应商
3.5 OMARA投标供应商赢者确定方法步骤

4 算例分析

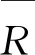

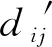
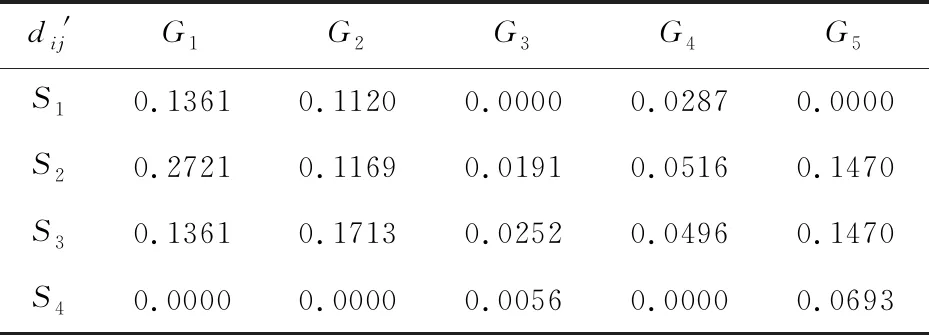







5 稳健性分析
5.1 投标属性值差异较大情形下算例计算结果的比较分析







5.2 不同距离公式下的算例结果的比较分析



6 结语

